站在微观的角度,这三个现象从理论上来说都是光与原子中的电子发生相互作用的结果,并且这种相互作用可以完全用量子电动力学来描述。对于散射,从经典角度,在入射光的激励下原子会产生与入射光频率相同的感生电偶极矩,根据经典电动力学的理论,这个振动的电偶极矩将会向外辐射同频率的电磁波,这就是瑞利散射,它是一种弹性散射过程。与之相应的,还有非弹性的拉曼散射,这种散射发生在入射光的频率和分子某一本征振动模式的频率接近时,光子将与分子振动能级发生相互作用,产生能量交换使得散射光子的能量可以降低或者升高
。当然,当入射光的频率足够高时,还能直接与原子的外层电子发生弹性散射(对,就是大家熟悉的高中物理选修 3-5 里的康普顿散射)。
反射与折射则是另外两种生活中常见的光学现象。这两个现象利用宏观上的麦克斯韦方程组以及界面处的边界条件可以完美地得到解释。当然,另一方面我们知道介质是由大量原子构成的,并且光子会与介质中的原子发生电磁相互作用,那么一个关键的问题就是这种微观上的电磁相互作用是如何导致光在介质中的行进速度变慢的?(或者说介质有折射率的呢?) 在尝试解释这个问题之前,我必须告诉大家,在量子的世界里,粒子的传播没有经典世界里那么“拘束”,事实上,它们可以走任何路径,但每个路径会伴随一个复数振幅,而我们观测到的结果是所有路径的复振幅求和的结果。如此一来,真空中的光子不必沿着直线传播,只不过那些不是直线的路径的复振幅振荡地非常剧烈,求和时相互之间抵消地非常厉害,以至于只有直线与其附近的路径保留了下来,这就是为何我们观测到真空中光子走直线的原因。当光子在透明介质里传播时,它除了自由传播还可能与介质中的原子发生相互作用即被散射。下面我们考察一下透过介质的光子究竟发生了什么事情?首先有一个振幅相应于光子直线穿过介质,没有发生任何散射,这个振幅将是最主要的,故而在复平面上,它的长度最长。但是,光子还有其它的路径到达介质下面的探测器 B:光子可能到达 X1 并散射出一个新光子传播到 B 处,同样的事情也能在 X2 处发生等等。因为这些路径都包含介质内一个电子散射一个光子的过程,故而它们的振幅长度是相同的,另一方面这些振幅都指向同一个方向,因为只经历一次散射的这些路径的长度都是相同的。这些小振幅与无散射直接到 B 的主振幅的夹角成 90°(为何是 90°?这个问题并不显然,当然我们可以“曲线救国”,说:“是因为我们考虑的是透明材料,介质不吸收光子,于是小振幅与主振幅的夹角必须为 90°!”),这些小振幅与主振幅相加,结果是最终振幅的长度与主振幅一样,但在复平面上额外多旋转了一个角度,这意味着光经过透明介质时,强度没有改变,但却积累了额外的相位!光在通过介质时最终振幅额外旋转的程度可以被称为该介质的“折射率”。
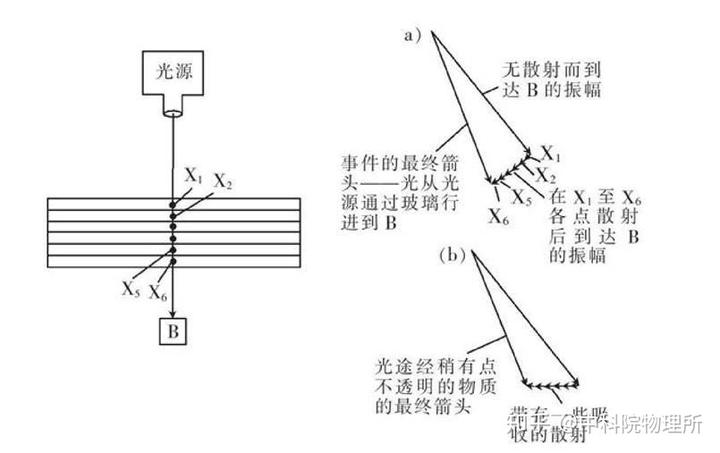
好了,我们已经从微观上知道折射率是如何产生的了,之后便可以用我们熟知的惠更斯原理或者费马原理得到正确的折射定律。事实上,即便是从路径积分的角度考虑,由于不同路径之间的复数振幅的幅角差异巨大,使得求和时这些振幅强烈地互相抵消,最终会只剩下最短路径的贡献(这是因为最短路径附近的路劲的振幅幅角变化不大,大体都指向同一个方向,故而只有它们在求和时没有抵消),因而这个结果与费马原理符合的很好!
类似地,反射现象也能从这样的微观原理去理解,更多的细节还是请参阅大名鼎鼎的物理学家费曼所写的《QED:光和物质的奇妙理论》吧,全书没有一个公式,靠一堆箭头解释了量子电动力学。这样神奇的书我想也只有费曼能写出来了 Orz。
至于题目里提到的单色光和非单色光,实际上,非单色光就是一些不同频率的单色光的叠加而已,本质并没有什么不同。
参考文献:
[1] Feynman, A. Zee. The Strange Theory of QED

 微信扫一扫
微信扫一扫 



