2019.10.31 更新,非常感谢楼下的某匿名大佬提供的公式代码,感谢!
从本质来说,第一类曲线曲面积分,以及重积分,其实都是多元数量值函数的积分,而第二型曲线曲面积分,属于多元向量值函数的积分。
这样说可能过于抽象了,下面具体解释一下为什么曲线积分有两类,以及两类之间的区别与联系(正如大佬所说,有些地方不严谨,但是我尽量讲的足够通俗,至少争取各位看官都能看懂)
一、从物理背景看曲线积分为何有两类
1.不均匀平面弯杆的质量
假设 L 为 xoy 面上的一个密度不均匀分布的弯杆,设 L 的方程为 y=y(x),其上任意一点的密度为μ(x,y),且μ为连续函数。为计算弯杆总质量 M,我们先利用 L 上 n-1 个点将其等分成 n 份,每一段小弧长度用 ds 表示。只要 n 充分大,那么每一小段的密度μ可以近似视为常量,从而利用微元法,我们可以轻松得出,总质量为
这种积分,我们将其称为(平面)第一型曲线积分。
2.变力沿曲线做功
假设平面 xoy 上有一物体 M,受到变力 F(x,y)的作用,沿着曲线 L,从 A 点运动到了 B 点,如何求变力 F 所做的总功呢?我们采取的方法是
“力的正交分解”+“微元法”
首先,我们将力 F(x,y)正交分解为水平方向的分力 P(x,y)和竖直方向的分力 Q(x,y),那么很明显,合力 F 所做的总功,等于水平方向分力 P(x,y)所做的功和竖直方向分力 Q(x,y)所做的功(注意,功是标量,本身没有方向,我们分解的只是力!)
然后采用我们之前在计算“不均匀平面弯杆的质量”时用过的微元法 ---- 取 L 上 n-1 个点将其等分成 n 份,每一段小弧长度用 ds 表示。只要 n 充分大,那么每一小段的分力 P 和 Q 均可以近似视为常量,与 x,y 无关。从而利用微元法,我们可以轻松得出,水平方向分力 P 所做的总功为 W1=∫P(x,y)dx,积分域为 L;竖直方向分力 Q 所做的总功为 W2=∫Q(x,y)dy,积分域也为 L,所以变力 F 沿曲线 L 从 A 到 B 所做的总功为
这种积分,我们将其称为(平面)第二型曲线积分。
综上,我们可以看出,因为实际问题的需要,我们将曲线积分分为了第一型和第二型。它们之所以都叫曲线积分,那是因为二者的积分域均为曲线 L;之所以又有区别,那是因为二者所解决的问题不同,第一型曲线积分是为了计算不均匀弯杆的质量,第二型曲线积分是为了计算变力沿曲线做功。
二、两类曲线积分的区别与联系
(一)区别
两类曲线积分之间的区别确实太多了。
首先,它们的背景意义不同,这便是重要区别之一;
其次,根据背景意义,我们可以轻松得出,第一型曲线积分,是没有方向性的,它不依赖于积分曲线 L 的走向(因为质量 M 与 L 的方向无关)。而第二型曲线积分的值,明显依赖与积分曲线 L 的方向(因为从背景意义来说,即使力的大小方向不变,但是物体如果沿着 L 从 B 到 A 反向运动,则 F 所做的功会变为相反数)
所以,有无方向性,是两类曲线积分之间的重大区别
(二)联系
二者的联系,可以从纯数学角度推导,具体推导过程此处略去,其转换公式为
其中,α和β是有向曲线 L 在点(x,y)的方向角。
下面,我从物理意义的角度来解释该转换公式为何成立——
我们采取两种不同的方式计算【变力沿曲线做功】的问题。
第一种方式便是第二类曲线积分,方法为“力的正交分解 + 微元法”,将力分解为水平方向的 P 和竖直方向的 Q,前文已有描述,此处不再赘述,只给出公式为
——①
第二种方式,是建立在第一种方法的基础上,区别只是将 P 和 Q 共同投影到了物体运动方向,如图所示
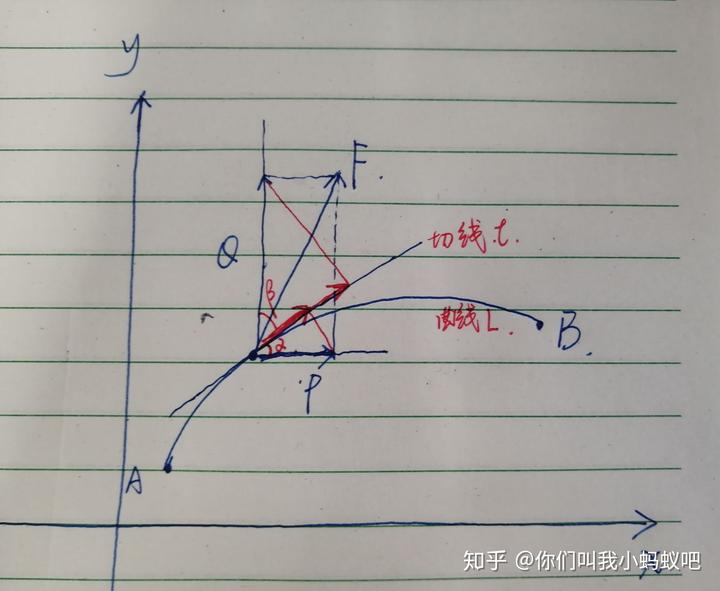
设有向曲线为 L,曲线在点(x,y)处切向量的方向角分别为α和β,切线记为 l。
为了算 F 所做总功,先将 F 正交分解为 P 和 Q,再将 P 和 Q 投影到物体运动方向。根据图示,P 在 l 方向的投影力的大小为 Pcosα,Q 在 l 方向的投影力的大小为 Qcosβ,所以合力 F 在运动方向的分力大小等于:
再次使用微元法,我们可以轻松得出力 F 所做的总功为
——②
由①②立得
最后,再次感谢楼下的匿名大佬提供的公式代码。

 微信扫一扫
微信扫一扫 



