在一本旧书[1]里看到一个非常直观的解释,分享在这里。

首先以一个最简单的例子开始。规定参与卷积的两个元素
和
分别是如下所示的两个方波:
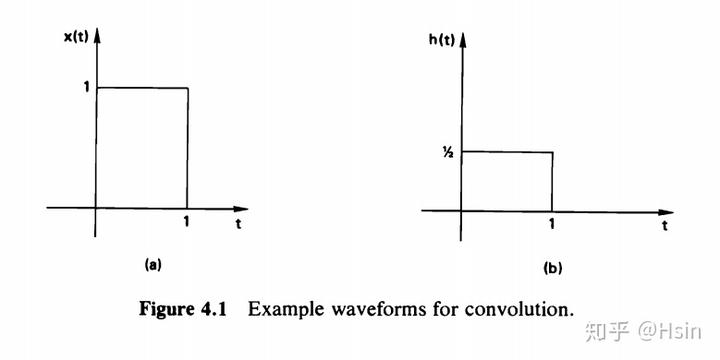
为了得到卷积表达式
中的形式,我们需要看看
和
长什么样。因为是对
积分(
),所以先将
和
的符号
改写成
。接下来,对元素
进行以下变换得到
:
- 翻转
得到
;
- 平移
得到
。
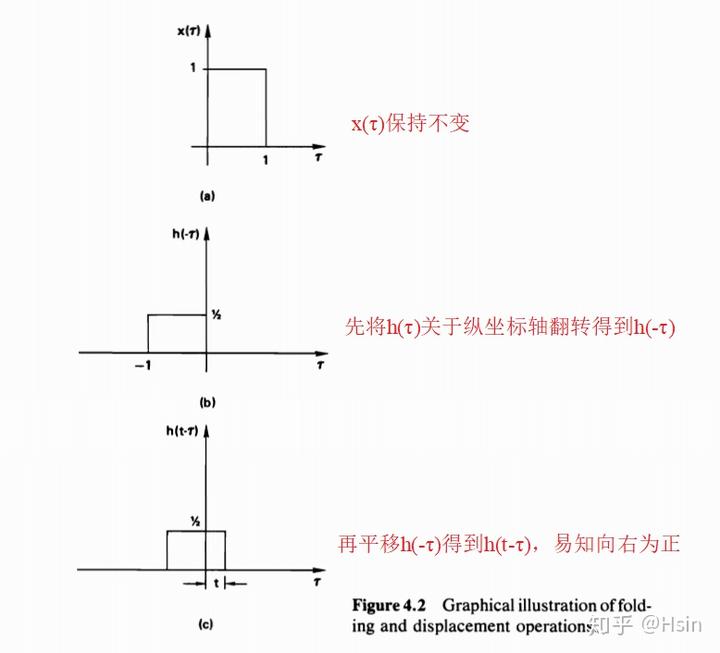
对于任意的
,都存在一个对应的
的图像。固定某个
,将
沿着横坐标轴从左到右与
相乘并积分,即为卷积
,也恰好是下图所示的阴影部分面积(不同的
的值对应着不同大小的阴影部分面积):
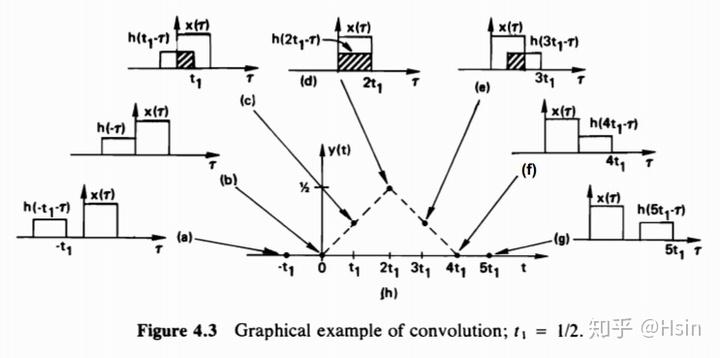
最后将所有
的取值综合起来,便是上图 (h) 所示的关于
的一个函数,这个函数便是卷积
的结果。
上面的思考(可视化)过程可以归纳为:
- 翻转;
- 平移;
- 相乘;
- 积分。
为了进一步熟悉这个流程,我们继续介绍一个稍微复杂一些的例子:
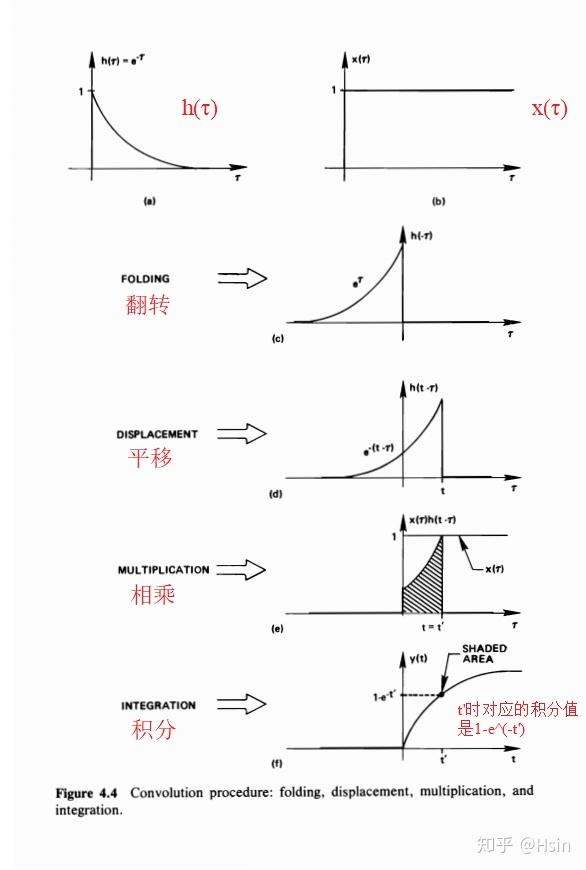
直接计算这个卷积,也可以验证上述结果的正确性:
实际上卷积有两种形式,既可以用
卷
,也可以用
去卷
,即
。体现在图像上面,我们也可以翻转 + 平移
,然后去求与
相乘后的积分。
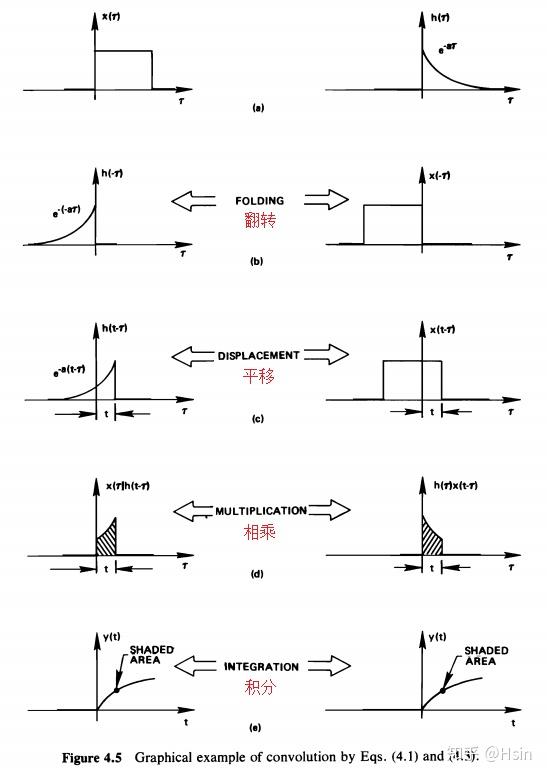
可以看到,这两种卷积路径的最终结果是相同的。
对于二维卷积(图像),用同样的思路也可以在头脑中形成一个很直观的印象,不妨思考一下。

 微信扫一扫
微信扫一扫 



