麻将牌的构成
麻将牌是由下面的牌组成:
1.万字牌:1-9 共 9 张(每个数字各一张)比如 1 万 2 万 3 万等
2.条子牌:1-9 共 9 张(每个数字各一张) 比如 1 条,2 条,3 条等
3.筒子牌:1-9 共 9 张(每个数字各一张) 比如 1 筒,2 筒,3 筒等
4.字牌:东南西北风各 4 张,红中、发财、白板各 4 张。
由基本牌组合而成的 万,条,筒的牌的数目为 4* 9 * 3 = 108。 由字牌组成的牌的数量为 4 * 7 = 28 。
所以整副牌就由 136 张牌组成。花牌(春夏秋冬)等不计算。
麻将的碰,杠,吃,听,胡
碰、杠、吃是麻将游戏中常用的三种操作,以便于玩家将手中的牌进行组合,以尽可能地增加胡牌的机会。具体意义如下:
碰:当玩家手中有两张相同的牌,而桌上已有一张相同的牌时,玩家可以选择碰此牌,即将自己手中的两张相同的牌与桌上的一张相同的牌组成一个刻子。
杠:当玩家手中有一张牌,而桌上已有三张相同的牌时,玩家可以选择杠此牌,即将自己手中的一张牌与桌上的三张相同的牌组成一个杠。这里面杠有多种,在算法中一定要注意处理。 具体分类如下:
弯杠:当自己手中有两张牌,别人打出一张牌自己进行了碰操作,然后自己又摸到了一张牌,形成了杠
明杠:自己手中有 3 张牌,别人打出一张牌,形成的杠
暗杠: 自己摸到了 4 张一样的牌为暗杠
吃:当桌上有玩家打出一张牌后,其他玩家如果手中有两张数字连着的牌,就可以选择吃此牌,即将桌上的牌和手中的牌组合成一个顺子。
听:听牌是麻将游戏中的一个术语,指的是在某一时刻,手牌中的牌差一张即可和牌,当前的手牌一定是 3n+1 张。
胡:在麻将游戏中,“胡”指的是牌手通过组成某些牌型,使结束时所剩余的牌组满足胡牌规则,从而赢得游戏的过程。
麻将胡牌条件
麻将想要胡牌,必须得满足一个条件就是 3n + 2
3 指的是由 3 张牌组成的面子( 顺子或者是刻子)
n 是指由 n 个(大于等于 0)组成的面子
2 指的就是由 2 张牌组成的将,这个将是必不可少的,面子可以不存在,但是将必须得存在,也就是说 n 可以为 0,但是 2 必须存在。如下图所示:
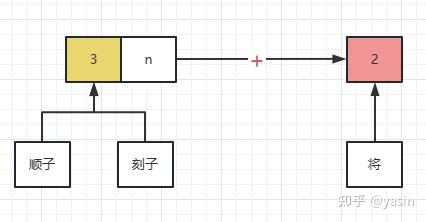
举个例子,当手牌为 14 张时 正好满足 3n +2 3x4 + 2 = 14 。表示由 4 组面子和一对将组成的手牌。再举个例子当手牌为 1 万 1 万 1 万 5 万 5 万 也是满足 3n+2,也可以满足胡牌的条件。
胡牌算法简介
胡牌算法实现起来有多种多样,但是大致分为两种,一种是使用回溯算法,一种是查表法。
查表法是利用事先生成好的所有的胡牌牌型,然后将这些牌型加载到内存中,直接在内存中对比即可,效率非常快,缺点只不灵活,需要事先按规则生成好表。
我们现在介绍的这种算法也是用到了回溯算法,我们称之为 “选将拆分法” 。
我们先把手牌中所有可能做将的牌先找出来,然后去掉这组将牌,看剩下的牌是否能满足 3n 条件,如果可以满足则可以胡牌,如果不能满足则不能胡牌。
这种算法中间利用适当的“剪枝” ,执行起来效率非常的快,同时这种算法对于处理任意赖子的效率也是很强悍,不比查表法慢。
我后面会逐步的分析如何这种算法,让任何没有基础的人都可以彻底掌握这种算法。我们当前介绍的是普通情况下的胡牌,不计算赖子的情况下。赖子的算法我们放在下一篇来讲,只要掌握了这种算法的原理,对于赖子的牌型算法也会很容易理解。
选将拆分法
选将拆分法就是将手牌中所有可能做将的牌,也可以说任意的牌,只要它的数量大于 2,那么它都可以是将。
我们先把这些可以做将的牌单独的列举出来。然后利用回溯法开始遍历这些将,首先将此将牌从手牌中移除,然后判断剩余的牌是否能满足 3n。如果可以满足那么就可以胡牌。当所有的将牌都遍历完了却没有满足 3n,则这副手牌不能胡牌。
算法数据结构
构建数据结构
在前面我们己经讲述过了,牌一共为136 张,万,条,筒各 9 种类型合计共 27 种类型,字牌共 7 种类型,所以牌的类型总体加起来就是 34 种类型。
因此我们可以使用一个数组来保存整副牌的数据结构。数组的下标用来表示当前牌的类型,数组的值用来表示当前类型的个数。因此我们就可以得出如下的数据结构:
int[] cards = {
2,0,0,0,0,0,0,0,0, //-- 1-9 万
0,0,0,0,0,0,0,0,0, //-- 1-9 条
0,0,0,0,0,0,0,0,0, //-- 1-9 筒
0,0,0,0,0,0,0 //- 东南西北中发白
};
我来举个简单的例子来帮助大家理解下这个数据结构,当前数据结构中数组的下标 0的值为 2,这就是表示 1 万这张牌的个数是 2。
数据结构使用
我们为什么使用这种数据结构而不使用其它的数据结构来构造整副牌呢?主要原因有下面几个,我会逐一为大家阐述清楚。
牌花色的获取
使用此数据结构可以非常方便的知道任何一张牌所属的花色。我们使用 下标索引 除以 9可以得出当前牌所属于的花色,比如 0/9 =0 ,9/9 =1 ,18/9=2 ,27/9 = 3 我们可以得出在数据结构中 万,条,筒它们的花色分别为 0 ,1 ,2。
获取某一花色的牌值
使用此数据结构可以非常方便的获取任何一种花色上面所有的牌,除了字牌为每种花色的牌都是 9 张,所以可以使用 (i / 9) * 9 获取此花色的最小值 ,然用用最小值加 8 就是最大值。
示例代码如下:
int min = (i / 9) * 9;
int max = min + 8;
if (max == 35) max = 33;
注:这上面的这段代码中因为字牌它的类型共有 7 种,所以我们需要特殊处理下。
获取某一张牌相邻牌
便捷的查找一张牌它左右的牌,到时用来判断是否可以形成顺子。
算法代码实现
基础代码校验
有了上面的阐述,我们可以写一个简单的胡牌的方法,方法的参数接收的是我们上面说的数据结构造成的手牌数组,这个方法返回一个 boolean 类型用来判断是否可以胡。代码如下:
/**
* 判断手牌是否可以胡牌
* @param handCards
* * 手牌的格式必须转换为如下数据格式,数组的下标表示牌的类型共 34 种类型,数组的值表示这个类型牌的数量
* cards[0] = 2
* 1 万 共有 2 张
* int[] cards = {
* 2,0,0,0,0,0,0,0,0, //-- 1-9 万
* 0,0,0,0,0,0,0,0,0, //-- 1-9 条
* 0,0,0,0,0,0,0,0,0, //-- 1-9 筒
* 0,0,0,0,0,0,0 //- 东南西北中发白
* };
*
* * @return */ public static boolean checkHandCardsCanWin(int[] handCards) { int[] cards = new int[34]; int cardsCount = 0; for (int i = 0; i < 34; ++i) { cards[i] = handCards[i]; cardsCount+= handCards[i]; } // 当手牌数量不满足 3n+2 时不构成胡牌条件 if (!(cardsCount >= 2 && cardsCount <= 14 && (cardsCount - 2) % 3 == 0)) { return false; } boolean hu = false; return hu; } 上面的这段代码就是增加了一个基础的判断,所有类型的牌的数量和是否满足 3n+2
选将代码实现
下面我们修改这段代码增加选将的代码。选将的方法就是遍历所有的牌型然后找出牌的数量大于等于 2 的牌当作将。
我们在遍历的同时也需要特殊的处理下一些特殊的牌。我们看一组下面的牌型(W 表示万 T 表示筒)

这组牌中有一对将 就是 5T,如果我们使用上面分析的选将拆分法,将 5T 进行拆分出来,然后遍历剩下的牌看是否能够成胡牌,这样子的思路也是可行的。但是我们仔细观察 1W 9W 这两张牌,这两张牌它左右,再或者 左左 右右都没有相邻的牌,所以它是一张散牌,必定无法胡牌。
所以我们在遇到这种散牌的时候,可以直接判定它无法胡,无需再进行下面的判定,提高算法效率。
增加之后的代码如下:
/*
* 用来存储所有可以做将的牌型
*/
List eyeList = new ArrayList<>();
/*
* 遍历所有的牌类型,找到牌的数量大于等于 2 的牌
*/
for (int i = 0; i < 34; ++i) {
// 这种类型牌最小值
int min = (i / 9) * 9;
// 为种类型牌最大值
int max = min + 8;
// 字牌的特殊处理,字牌的个数为 7 而其它类型数量为 9
if (max == 35) max = 33;
if (cards[i] == 1 &&
(i - 2 < min || cards[i - 2] == 0) &&
(i - 1 < min || cards[i - 1] == 0) &&
(i + 1 > max || cards[i + 1] == 0) &&
(i + 2 > max || cards[i + 2] == 0)) {
// 这种散牌直接无法胡,除非有赖子牌的情况下
return false;
}
if (cards[i] >= 2) {
eyeList.add(i);
}
}
上面的这段代码在判断散牌的处理上,首先判断了每种花色的范围,确保这张牌的上一张,上上张,下一张,下下张都在它所属的花色范围内,并且数量为 0,这样子才能证明这张牌没有任何相邻的牌,是散牌。
下一步我们就是将选举出来的将,从手牌中去除,然后利用回溯法来判断牌型是否满足胡牌条件了,代码如下所示:
/*
* 遍历所有的将来判断是否可以胡
*/
boolean win = false;
/*
* 如果没有任何的将直接断定无法胡牌
*/
if (eyeList.size() == 0){
return false;
}else{
for (int i = 0; i < eyeList.size(); i++) {
// 将牌所在牌数组中的索引,后面可以根据这个索引直接从牌数组中获取牌的数量
int eyeIndex = eyeList.get(i);
// 获取将牌的数量
int n = cards[eyeIndex];
// 首先将[将牌]从牌堆中移除,当此将无法完成胡牌条件时,在将此牌放回牌堆,利用回溯法再进行判定下一张将牌
cards[eyeIndex] -= 2;
win = handleCardsWithoutEye(cards);
cards[eyeIndex] = n;
if (win) {
break;
}
}
}
return win;
上面这段代码首先判断了如果将列表为空的情况下直接返回 false,无法胡牌,如果将列表不为空的情况下开始遍历所有的将,先把将从手牌中去掉,然后判断接下来的牌是否会胡牌,如果能胡则直接跳出迭代,否则在将这张将牌加入到手牌中。然后继续利用回溯算法,不断的迭代,直到找到满足胡牌条件的牌型,或者是所有的将全部迭代完毕后依然没有找到胡牌,则此副手牌不能构造胡牌。
每种花色胡判定
OK,下面我们继续开始写 handleCardsWithoutEye 这个方法。这个方法就是用来判定除去将之外的牌是否可以构造胡牌条件。
因为手牌中己经去除了将牌,所以如果当前的手牌构成 3n 那么就构造了胡牌的条件。
我们知道,手牌当中可能包含 万,条,筒,字 四种不同的花色,如果说每一种花色可以满足胡牌的条件即满足 3n ,那么整体肯定是满足 3n 条件的。这种思想就是分而治之的思想。
代码如下所示:
private static boolean handleCardsWithoutEye(int[] cards) {
/*
* 遍历万,条,筒三种花色依次判定此种花色是否可以构造胡牌条件,如果每种花色都可以构造胡牌条件 3n 则此手牌一定可以胡
* 这里利用的是分而治之的思想
*/
for (int i = 0; i < 3; i++) {
/*
* 遍历手牌中指定花色的牌
*/
boolean win = checkNormalCardsWin(cards, i * 9, i * 9 + 8);
if (!win){
return false;
}
}
/*
* 处理字牌花色,字牌的花色为 3
*/
return checkZiCardsWin(cards);
}
上面的代码就是分开来讨论万,条,筒,字和字牌,每种花色是否满足 3n 条件,如果有任意一种不满足则无法胡牌。代码中通过调用 checkNormalCardsWin 将当前花色的取值范围传入方法中,由此方法校验当前花色是否满足 3n。
我们用如下的牌型给大家演示下调用的过程,帮助大家理解下原理。(W 表示万 T 表示筒)

我们从上面的牌型中可以得知,将一共有两个分别是 1W,5T 。下面我们分别选取不同的将来演变下过程。
当 1W 为将时:
因为将的花色是万字花色,需要将 1W 从手牌中去除掉。然后分别遍历 3 种不同的花色,结果如下:
万(4W,5W,6W):满足 3n
筒(1tong,2tong,3tong):满足 3n
条(1T,2T,3T,4T,5T,5T):不满足
当 5T 为将时:
将 5T 从手牌中去除掉,然后分别遍历 3 种不同的花色,结果如下:
万(1W,1W,4W,5W,6W):不满足 3n
筒(1tong,2tong,3tong):满足 3n
条(1T,2T,3T,4T):不满足
不知大家有没有发现,无论是哪种花色为将,都将遍历三种花色,不过由于当前将牌的花色由于去掉了将所以牌不是完整的,但是其它的两种花色的牌是完整的。也就是说我们可以将其它的两种花色缓存起来,当下次的将如果还是万花色,那么我们可以直接获取 条,筒两种花色的判定结果。
缓存的思路就是将当前非将牌的花色的判定结果进行缓存,所以当如果换了将之后,我们直接取非将花色的判定结果,无需进行计算。
如当前我们先遍历的是 1W 的将,所以我们可以将筒,条两种花色进行缓存。
在遍历 5T 将时,我们可以直接从缓存中获取 万,条两种花色的缓存的值,由于在缓存中只有条花色的缓存,所以条花色的判定结果可以直接从缓存中获取。
花色胡判定缓存
根据上面我们分析的思路我们可以修改下代码加入缓存。这里我们使用一个数组来保存每种花色的判定结果
int[] checkedCache = {0, 0, 0, 0};
使用数组的下标索引来保存花色,值来保存判定结果,在这里我们使用 0 表示未判定 1 表示成功 2 表示失败。
好的,我们按上面的思路修改下我们的代码,修改后的 handleCardsWithoutEye 代码如下:
/**
* 将手牌分开不同的花色进行分别判定,如果万,条,筒,字牌每种花色都能满足胡牌条件则此手牌一定可以胡
* @param cards hand cards
* @param eye_color
* @param checkedCache
* @return whether can hu
*/
private static boolean handleCardsWithoutEye(int[] cards,int eyeColor, int[] checkedCache) {
/*
* 遍历万,条,筒三种花色依次判定此种花色是否可以构造胡牌条件,如果每种花色都可以构造胡牌条件 3n 则此手牌一定可以胡
* 这里利用的是分而治之的思想
*/
for (int i = 0; i < 3; i++) {
/*
* 参数中传入的将的花色是否和当前遍历的花色一样,如果一样则不处理,如果不一样则将其它花色的胡的判定结果存储起来
* 方便下次在遍历同样花色的将的时候,其它的花色的判定直接从缓存中获取不需要在重新的判定,提升算法效率
* 比如当前传入的将为 7 万 我们可以把 条,筒两种花色的判定结果保存起来
* 当传入的将为 8 万时 我们可以直接从缓存中获取到其它 条,筒花色的判定结果无需重新判定
*/
int cacheIndex = -1;
if (eyeColor != i) {
cacheIndex = i;
}
/*
* 遍历手牌中指定花色的牌
*/
boolean win = checkNormalCardsWin(cards, i * 9, i * 9 + 8,cacheIndex,checkedCache);
/*
* 当前花色如果不是传入的将的花色则将判定结果进行存储 1 表示判定成功 2 表示判定失败
*/
if (cacheIndex >0 && win){
checkedCache[i] = 1;
}
if (cacheIndex >0 && !win){
checkedCache[i] = 2;
}
if (!win){
return false;
}
}
/*
* 处理字牌花色,字牌的花色为 3
*/
int cacheIndex = -1;
if (eyeColor != 3){
cacheIndex = 3;
}
return checkZiCardsWin(cards,cacheIndex,checkedCache);
}
上面的代码将每种非当前将牌的花色进行缓存,向缓存中放置值是由方法 checkNormalCardsWin 来实现的,同时此方法也是重点处理每种花色是否满足 3n 的核心逻辑方法。
下面我们开始分析如何实现此方法。
万条筒花色胡判定逻辑
checkNormalCardsWin 前面己经讲过主要是用来处理某一花色是否满足 3n 条件。这个方法接收的参数有 手牌 cards,此花色开始花色索引,结束索引。有了这些我们就可以获取到此花色中所有的牌。
比如有一幅手牌它如下所示:

它用我们算法中的数据结构表示如下:
int[] cards = {
2,1,1,1,1,1,1,0,0, //-- 1-9 万
1,1,1,1,1,1,0,0,0, //-- 1-9 条
0,0,0,0,0,0,0,0,0, //-- 1-9 筒
0,0,0,0,0,0,0 //- 东南西北中发白
};
我们获取到万花色的索引为 0-8,获取到的牌为 2,1,1,1,1,1,1,0,0 ,我们根据数字所在数组中的索引和具体的值就可以得出所需要的所有信息。接下来我们就要对这些数字进行加工,判断是否满足 3n 。
由于这些数字是组数中的一部分,操作起来不太方便,我们可以将这些数字提取出来,我们将这些数字按照它在数组中的索引位置,将它组成一个数字方便后面的判定运算。
因为万,条,筒每种花色都有 9 张牌,所以我们可以使用一个 9 位数的数字来表示这个花色,这个数字从低位到高位分别保存 1 万 -9 万 或 1-9 条 1-9 筒,位数表示牌的类型。
比如个位表示 1 万 十位表示 2 万 千万表示 3 万,而位数上面的值表示牌的数量。
这其实和我们之前使用数组的道理是一样的,数组的索引表示牌类型,数组的值表示此牌的个数。
举个例子,如下这个数字 001111112 它表示有 【2 个 1 万 1 个 2 万 1 个 3 万 1 个 4 万 1 个 5 万 1 个 6 万 1 个 7 万 0 个 8 万 0 个 9 万】示意图如下所示:
0 0 1 1 1 1 1 1 2
9 万 8 万 7 万 6 万 5 万 4 万 3 万 2 万 1 万
将数组中的这些数字组合成一个数字也比较容易,代码如下:
int n = 0;
for (int i = beginIndex; i <= endIndex; i++) {
n = n * 10 + cards[i];
}
就是每次在循环值的时候,都将这个值放置在数字上面的一个高位上面。
好了,分析完上面的逻辑,我们现在可以写一个完整的 checkNormalCardsWin 方法了,代码如下所示:
/**
* 检查当前花色是否满足胡牌条件 即是否满足 3n
* @param cards 手牌
* @param beginIndex 当前花色开始索引
* @param endIndex 当前花色结束索引
* @param cache_index 要查询的缓存的花色索引
* @param checkedCache 缓存
* @return 是否可以胡 true / false
*/
private static boolean checkNormalCardsWin(int[] cards, int beginIndex, int endIndex,int cacheIndex, int[] checkedCache) {
/*
* 如果当前要判定的花色与将的花色一样那么 cacheIndex 值为 -1,不从缓存中获取
* 否则从缓存中拿判定的结果,无需重新判定
*/
if (cacheIndex >= 0) {
int n = checkedCache[cacheIndex];
if (n > 0) {
return n - 1 == 0;
}
}
/*
* 将当前花色中所有的牌组成一个数字,方便后面进行判定.因为万,条,筒每种花色都有 9 张牌,所以我们可以使用一个 9 位数的数字来表示这个花色
* 此数字从低位到高位分别保存 1 万 -9 万 或 1-9 条 1-9 筒,位数表示牌的类型,比如个位表示 1 万 十位表示 2 万 千万表示 3 万,而位数上面的值表示牌的数量
* 这其实和我们之前使用数组的道理是一样的,数组的索引表示牌类型,数组的值表示此牌的个数
* 举个例子,如下这个数字 101000111 它表示有 1 个 1 万 1 个 2 万 1 个 3 万 0 个 4 万 5 万 6 万 1 个 7 万 0 个 8 万 1 个 9 万,示意图如下所示:
*
* 1 0 1 0 0 0 1 1 1
* 9 万 8 万 7 万 6 万 5 万 4 万 3 万 2 万 1 万
*/
int n = 0;
for (int i = beginIndex; i <= endIndex; i++) {
n = n * 10 + cards[i];
}
/*
* 0 表示此花色己经没有牌,满足 3n
*/
if (n == 0) {
return true;
}
/*
* 检查当前花色牌的数量是否满足 3n
* 由于 n 是由多张牌组成,我们要判断此数字上面所有位数上面的数字的和是否能被 3 整除
* 由简单的数学知识得知: 想要判断一个数字上面所有位数上面的和能被整除,只要此数字能被 3 整除即可
*/
if (n % 3 != 0) {
return false;
}
/*
* 开始拆分此数字 n,如果数字 n 可以被拆分成 n 个顺子或者刻子则可以胡
*/
return splitCards(n);
}
代码中的一些逻辑上面己经讲到了,我们就不在赘述了,我们将处理分割 这个数字 n 的逻辑放在一个新的方法 splitCards 来完成。因为我们在拆分的时候要用到迭代,所以这块的逻辑由一个单独的方法来完成。
下面我们开始分析下这个 splitCards 方法如何实现。这个方法接收一个由牌组成的数字,比如我们上面提及的由万字花色组成的数字 00111111 它表示有 【1 个 2 万 1 个 3 万 1 个 4 万 1 个 5 万 1 个 6 万 1 个 7 万 0 个 8 万 0 个 9 万】
我们在拆分时从数字的低位开始一直向高位拆除,看拆除下来的这个数字是否可以组成刻子,或者是与前面的数字组成顺子。如果可以则表示拆除成功。将拆分成功后的新数字继续使用迭代算法拆分,直到将这个数字拆除完毕。如果其中某一步无法拆除,则这组牌不能构成胡牌。我们每拆除一个数字用 P 表示 此数字前面的数字和前前面的数字我们使用 P1 ,P2来表示。
在拆除的时候要看这个数字来决定具体拆分为顺子,还是刻子。具体拆分规则如下:
当 P = 1 时 与前面的两个数字,拆分为 1 1 1 顺子
当 P =2 时 与前面的两个数字,拆分为 2 2 2 两个顺子
当 P = 3 时 直接拆分为刻子
当 P = 4 时 直接拆分为 1 和 3 所以 P = 4 时与 P=1 时为同样的处理
我们用上面的这个数字 00111111 举例演示下拆除过程,第一步取最低位上面数字 也就是 1 ,当 P=1 时拆分为 1 1 1 ,所以拆分后的数字为 00111000 ,然后继续拆分最终将这个数字拆分完毕,这个数字最终值为 0 表示完全拆分,这个花色的牌可以胡牌。
我们再使用一个新的数字,00111112 取最低位上面的数字即 2,当 P=2 时拆分为 2 2 2 ,但是 P 前面的两个数字分别为 1 1 所以无法拆分,所以这个花色所构成的牌无法胡。
我们分析完处理逻辑后,下面开始写这个方法,代码如下:
/**
* 拆分这个数字,直到无法拆分为止,当这个数字为 0 时表示可以完全拆除成功
* @param n
* @return
*/
private static boolean splitCards(int n) {
int p = 0;
while (true) {
if (n == 0) return true;
/*
* 找到低位数上不为 0 的数字
*/
while (n > 0) {
p = n % 10;// 获取个位数
n = n / 10;// 将 n 去掉低位数
if (p != 0) break;
}
/*
* 1 和 4 是一样的处理方法 4 可以拆分为 1 和 3,3 直接是刻子不用作处理
*/
if (p == 1 || p == 4) {
return singleNumHandle(n);
} else if (p == 2) {
return doubleNumHandle(n);
} else if (p == 3) {
// 刻字不用作处理
}
}
}
这个方法就是不断的利用迭代,不断的拆分这个数字 N 然后根据拆分下来的数字,使用不同的方法来处理。这里每拆分一次,这个数字 N 就会减少一个低位,直到这个数字为 0 为止。
下面我们开始写单个数字的处理代码,方法 singleNumHandle 代码如下所示:
private static boolean singleNumHandle(int n) {
// 获取此数字前面的 p1
int p1 = n % 10;
// 获取此数字前面的 p2
int p2 = (n % 100) / 10;
if (p1 == 0) {
return false;
} else {
n -= 1;
}
if (p2 == 0) {
return false;
} else {
n -= 10;
}
// 当 n ==0 表示此花色的牌完全满足 3n 法则 可以胡牌
if (n == 0) {
return true;
}
return splitCards(n);
}
2 个数字的处理代码,如下所示:
/**
* 尾数为 2 的处理方法,形式为 2 2 2
* @param n
* @return
*/
private static boolean doubleNumHandle(int n) {
// 获取此数字前面的 p1
int p1 = n % 10;
// 获取此数字前面的 p2
int p2 = (n % 100) / 10;
if (p1 < 2) {
return false;
} else {
n -= 2;
}
if (p2 < 2) {
return false;
} else {
n -= 20;
}
// 当 n ==0 表示此花色的牌完全满足 3n 法则 可以胡牌
if (n == 0) {
return true;
}
return splitCards(n);
}
以上两个方法分别为处理 P=1 P=2 的情况。代码中的处理逻辑也比较简单,就是比较 P 前面的两个数字 P1 P2 是否可以构成 111 ,2 2 2 这两种情况,如果可以造成则将 P, P1 ,P2 全部消除,然后使用这个新的数字继续迭代,继续判定,直到这个数字为 0 为止。
以上的代码就是全部处理万,条,筒三种花色的全部逻辑和代码。在这里我们要注意的是缓存那部分的逻辑,以及迭代拆分数字那部分逻辑,这部分逻辑是核心逻辑。
字牌花色胡判定逻辑
如果大家己经理解了上面讲的 万,条,筒花色的处理逻辑,那么对于字牌的处理逻辑就显得很简单了。因为字牌只能是组成刻子,所以我们只需要判定某一张牌的数量是否为 3 即可。当然了,有一些地方的玩法可能字牌之前可以组成顺子,那么就需要特殊处理了,处理方法参照上面万,条,筒花色的处理方法。
最终代码
下面为大家附上一个最终的代码
import java.util.ArrayList;
import java.util.List;
public class MahjongSplitEyeAlgorithm {
/**
* 判断手牌是否可以胡牌,使用选将拆分法来实现
* @param handCards
* * 手牌的格式必须转换为如下数据格式,数组的下标表示牌的类型共 34 种类型,数组的值表示这个类型牌的数量
* cards[0] = 2
* 1 万 共有 2 张
* int[] cards = {
* 2,0,0,0,0,0,0,0,0, //-- 1-9 万
* 0,0,0,0,0,0,0,0,0, //-- 1-9 条
* 0,0,0,0,0,0,0,0,0, //-- 1-9 筒
* 0,0,0,0,0,0,0 //- 东南西北中发白
* };
*
* * @return true 可以胡 false */ public static boolean checkHandCardsCanWin(int[] handCards) { int[] cards = new int[34]; int cardsCount = 0; for (int i = 0; i < 34; ++i) { cards[i] = handCards[i]; cardsCount+= handCards[i]; } // 当手牌数量不满足 3n+2 时不构成胡牌条件 if (!(cardsCount >= 2 && cardsCount <= 14 && (cardsCount - 2) % 3 == 0)) { return false; } /* * 用来存储所有可以做将的牌型 */ List eyeList = new ArrayList<>(); /* * 遍历所有的牌类型,找到牌的数量大于等于 2 的牌 */ for (int i = 0; i < 34; ++i) { // 这种类型牌最小值 int min = (i / 9) * 9; // 为种类型牌最大值 int max = min + 8; // 字牌的特殊处理,字牌的个数为 7 而其它类型数量为 9 if (max == 35) max = 33; if (cards[i] == 1 && (i - 2 < min || cards[i - 2] == 0) && (i - 1 < min || cards[i - 1] == 0) && (i + 1 > max || cards[i + 1] == 0) && (i + 2 > max || cards[i + 2] == 0)) { // 这种散牌直接无法胡,除非有赖子牌的情况下 return false; } if (cards[i] >= 2) { eyeList.add(i); } } /* * 遍历所有的将来判断是否可以胡 */ boolean win = false; /* * 如果没有任何的将直接断定无法胡牌 */ if (eyeList.size() == 0){ return false; }else{ int[] checkedCache = {0, 0, 0, 0}; for (int i = 0; i < eyeList.size(); i++) { // 将牌所在牌数组中的索引,后面可以根据这个索引直接从牌数组中获取牌的数量 int eyeIndex = eyeList.get(i); // 获取将牌的数量 int n = cards[eyeIndex]; // 首先将[将牌]从牌堆中移除,当此将无法完成胡牌条件时,在将此牌放回牌堆,利用回溯法再进行判定下一张将牌 cards[eyeIndex] -= 2; win = handleCardsWithoutEye(cards,eyeIndex / 9,checkedCache); cards[eyeIndex] = n; if (win) { break; } } } return win; } /** * 将手牌分开不同的花色进行分别判定,如果万,条,筒,字牌每种花色都能满足胡牌条件则此手牌一定可以胡 * @param cards hand cards * @param eye_color * @param checkedCache * @return whether can hu */ private static boolean handleCardsWithoutEye(int[] cards,int eyeColor, int[] checkedCache) { /* * 遍历万,条,筒三种花色依次判定此种花色是否可以构造胡牌条件,如果每种花色都可以构造胡牌条件 3n 则此手牌一定可以胡 * 这里利用的是分而治之的思想 */ for (int i = 0; i < 3; i++) { /* * 参数中传入的将的花色是否和当前遍历的花色一样,如果一样则不处理,如果不一样则将其它花色的胡的判定结果存储起来 * 方便下次在遍历同样花色的将的时候,其它的花色的判定直接从缓存中获取不需要在重新的判定,提升算法效率 * 比如当前传入的将为 7 万 我们可以把 条,筒两种花色的判定结果保存起来 * 当传入的将为 8 万时 我们可以直接从缓存中获取到其它 条,筒花色的判定结果无需重新判定 */ int cacheIndex = -1; if (eyeColor != i) { cacheIndex = i; } /* * 遍历手牌中指定花色的牌 */ boolean win = checkNormalCardsWin(cards, i * 9, i * 9 + 8,cacheIndex,checkedCache); /* * 当前花色如果不是传入的将的花色则将判定结果进行存储 1 表示判定成功 2 表示判定失败 */ if (cacheIndex >0 && win){ checkedCache[i] = 1; } if (cacheIndex >0 && !win){ checkedCache[i] = 2; } if (!win){ return false; } } /* * 处理字牌花色,字牌的花色为 3 */ int cacheIndex = -1; if (eyeColor != 3){ cacheIndex = 3; } return checkZiCardsWin(cards,cacheIndex,checkedCache); } /** * 检查当前花色是否满足胡牌条件 即是否满足 3n * @param cards 手牌 * @param beginIndex 当前花色开始索引 * @param endIndex 当前花色结束索引 * @param cacheIndex 要查询的缓存的花色索引 * @param checkedCache 缓存 * @return 是否可以胡 true / false */ private static boolean checkNormalCardsWin(int[] cards, int beginIndex, int endIndex,int cacheIndex, int[] checkedCache) { /* * 如果当前要判定的花色与将的花色一样那么 cacheIndex 值为 -1,不从缓存中获取 * 否则从缓存中拿判定的结果,无需重新判定 */ if (cacheIndex >= 0) { int n = checkedCache[cacheIndex]; if (n > 0) { return n - 1 == 0; } } /* * 将当前花色中所有的牌组成一个数字,方便后面进行判定.因为万,条,筒每种花色都有 9 张牌,所以我们可以使用一个 9 位数的数字来表示这个花色 * 此数字从低位到高位分别保存 1 万 -9 万 或 1-9 条 1-9 筒,位数表示牌的类型,比如个位表示 1 万 十位表示 2 万 千万表示 3 万,而位数上面的值表示牌的数量 * 这其实和我们之前使用数组的道理是一样的,数组的索引表示牌类型,数组的值表示此牌的个数 * 举个例子,如下这个数字 101000111 它表示有 1 个 1 万 1 个 2 万 1 个 3 万 0 个 4 万 5 万 6 万 1 个 7 万 0 个 8 万 1 个 9 万,示意图如下所示: * * 1 0 1 0 0 0 1 1 1 * 9 万 8 万 7 万 6 万 5 万 4 万 3 万 2 万 1 万 */ int n = 0; for (int i = beginIndex; i <= endIndex; i++) { n = n * 10 + cards[i]; } /* * 0 表示此花色己经没有牌,满足 3n */ if (n == 0) { return true; } /* * 检查当前花色牌的数量是否满足 3n * 由于 n 是由多张牌组成,我们要判断此数字上面所有位数上面的数字的和是否能被 3 整除 * 由简单的数学知识得知: 想要判断一个数字上面所有位数上面的和能被整除,只要此数字能被 3 整除即可 */ if (n % 3 != 0) { return false; } /* * 开始拆分此数字 n,如果数字 n 可以被拆分成 n 个顺子或者刻子则可以胡 */ return splitCards(n); } /** * 拆分这个数字,直到无法拆分为止,当这个数字为 0 时表示可以完全拆除成功 * @param n * @return */ private static boolean splitCards(int n) { int p = 0; while (true) { if (n == 0) return true; /* * 找到低位数上不为 0 的数字 */ while (n > 0) { p = n % 10;// 获取个位数 n = n / 10;// 将 n 去掉低位数 if (p != 0) break; } /* * 1 和 4 是一样的处理方法 4 可以拆分为 1 和 3,3 直接是刻子不用作处理 */ if (p == 1 || p == 4) { return singleNumHandle(n); } else if (p == 2) { return doubleNumHandle(n); } else if (p == 3) { // 刻字不用作处理 } } } /** * 单个数字的处理,需要拆分为 1 1 1 形式 * @param n * @return */ private static boolean singleNumHandle(int n) { // 获取此数字前面的 p1 int p1 = n % 10; // 获取此数字前面的 p2 int p2 = (n % 100) / 10; if (p1 == 0) { return false; } else { n -= 1; } if (p2 == 0) { return false; } else { n -= 10; } // 当 n ==0 表示此花色的牌完全满足 3n 法则 可以胡牌 if (n == 0) { return true; } return splitCards(n); } /** * 尾数为 2 的处理方法,形式为 2 2 2 * @param n * @return */ private static boolean doubleNumHandle(int n) { // 获取此数字前面的 p1 int p1 = n % 10; // 获取此数字前面的 p2 int p2 = (n % 100) / 10; if (p1 < 2) { return false; } else { n -= 2; } if (p2 < 2) { return false; } else { n -= 20; } // 当 n ==0 表示此花色的牌完全满足 3n 法则 可以胡牌 if (n == 0) { return true; } return splitCards(n); } /** * 字牌花色的处理逻辑 * @param cards * @param cacheIndex * @param cache * @return */ private static boolean checkZiCardsWin(int[] cards, int cacheIndex, int[] checkedCache) { /* * 如果当前要判定的花色与将的花色一样那么 cacheIndex 值为 -1,不从缓存中获取 * 否则从缓存中拿判定的结果,无需重新判定 */ if (cacheIndex >= 0) { int n = checkedCache[cacheIndex]; if (n > 0) { return n - 1 == 0; } } /* * 字牌的索引为 27 至 34 字牌的判定很简单因为字牌只能是组成刻子不能组成顺子,所以我们只需要判定此牌的个数是否为 3 即可 */ for (int i = 27; i < 34; i++) { int n = cards[i]; if (n == 0) { continue; } if (n != 3){ return false; } } return true; } public static void main(String[] args) { //1 万 2 万 3 万 1 条 2 条 3 条 1 筒 2 筒 2 筒 5 万 5 万 5 万 8 条 8 条 int[] case1 = { 1,1,1,0,3,0,0,0,0, //-- 1-9 万 1,1,1,0,0,0,0,2,0, //-- 1-9 条 1,1,1,0,0,0,0,0,0, //-- 1-9 筒 0,0,0,0,0,0,0 //- 东南西北中发白 }; boolean win = checkHandCardsCanWin(case1); System.out.println(win); } } 总结
现在我们把前面所讲的东西做一个小结。判定麻将胡牌的方法,主要考虑用到,回溯算法,分而治之思想。回溯算法用在遍历所有可能真正做将的牌,如果当前的将不是真正的将,那么回溯到下一个将,继续判定,直到找到真正的将,这块的逻辑也是整个算法的核心逻辑所在,在使用回溯算法时要注意适当的应用 “剪纸” 可以加快算法的执行效率。
而分而治之的思想主要是体现在将手牌分为不同的花色,分别讨论是否满足胡牌条件。如果所有的单个的花色都满足,那么整合也满足。
这个算法并没有涉及到赖子,如果有赖子的话,那么在选将的方法上面,分而治之讨论单个花色是否可以组成 N 个顺子,刻子时就要复杂一些。但是总体的思路是不变的。
下一节我们讨论如何完善此算法,支持任意赖子。

 微信扫一扫
微信扫一扫 



