这是一个非常好的问题,也说明一个一个反直觉的现象。之所以反直觉,也跟这个问题的本质有关。
神经网络这个问题具有一定的一般性,实际上我们可以把问题和现象的范畴放大,扩展到“动态系统”(Dynamical Systems), 也就是 状态 / 输出 随 时间 / 输入 变化的系统,按照系统内在机制,动态系统可以具体划归为“线性系统”和“非线性系统”,按照系统能用微分方程还是差分方程表示,可以划分为“连续动态系统”和“离散动态系统”。
显然地,神经网络属于动态系统的一个很小的子范畴——离散非线性动态系统[1]. 离散是显然的,又由于神经网络中一般包括大量的非线性过程,比如 ReLu 这样的非线性激活函数,DropOut,Gate 等等.
线性系统按照输入而非时间可以表示为
, 也就是可以用线性方程表示. 对于这样一个 系统,如果在输入上叠加一个随机噪声(高斯分布、均匀分布 等)
, 则输出为
, 对应的输出噪声为
. 在这样的系统中,噪声是不可能在输出中消失的,也就是说,线性系统必然不能容错. 而线性系统很常见也很容易直观理解,因此非常符合“直觉”.
对于非线性系统,情况会有显著的不同[2][3]. 在细说之前,我们先举一个直观的例子:
对于非线性系统
, 输入 x 符合伯努利分布(p=0.5)上叠加一个
的噪声,那么这个噪声输入在接近 50%情况下对输出没有影响,也就是表现出容错性.
在这个容错性的例子中我们看到,数据
的跟随机噪声
独立且非同分布,而非线性系统放大了二者的差异。 这种数据跟噪声的分布不同的情况在神经网络的输入中几乎是必然满足的. 而且神经网络通常包含大量这样的非线性过程,或者说“非线性滤波器”(Nonlinear Filters)[4].
在神经网络对图像信号处理中,其每个非线性滤波器都可以等价转化成傅立叶平面滤波器(Fourier Plane Nonlinear Filters)的组合形式. 这样滤波器的阶数
就代表了滤波器的非线性程度. 随着非线性程度的增加,这个滤波器输出的信噪比
也会增加[5].
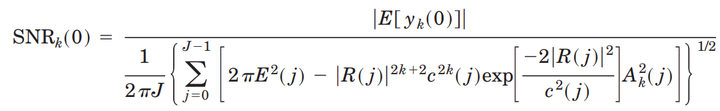
在问题设置的比较好的情况下,神经网络在训练过程中,其输出跟数据标签
的相关性会持续增加,跟数据 X 中的随机噪声的相关性在不出现明显过拟合的情况下不会发生变化。这个过程也决定了,神经网络中的非线性滤波器在训练过程中会不断优化其参数,提高对噪声的鲁棒性.
实际上,在神经网络训练中,在 X 上叠加适当水平的噪声,对训练结果的泛化性(Generation)有好处,这种噪声叠加等价于吉洪诺夫正则化(Tikhonov regularization)[6], 可以让神经网络的输出关于输入 X 更加平滑[7].
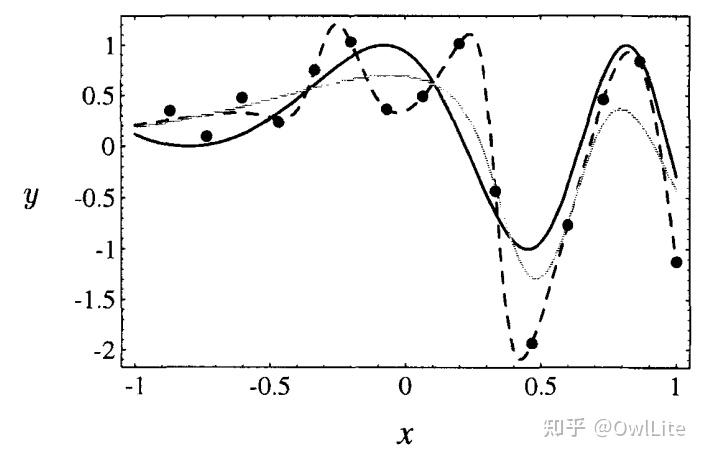
这在某种程度上等价于做 Data Augmentation.

 微信扫一扫
微信扫一扫 



