(1/1)^2+(1/2)^2+(1/3)^2+……=(π^2)/6，为什么结果与 π 有关？

2023-07-19 06:00:26 • 网络百科

3Blue1Brown 给了一个非常漂亮的几何解释：大概思路是用反比平方定律把问题物理化。假设你在一个周长为 2 的圆形湖上，其直径为

$d=2/\pi.$

假设你在这个环形湖对面有个点光源，那么根据反比平方定律，你感知的光线强度就是

$I\sim1/d^2=\pi^2/4.$

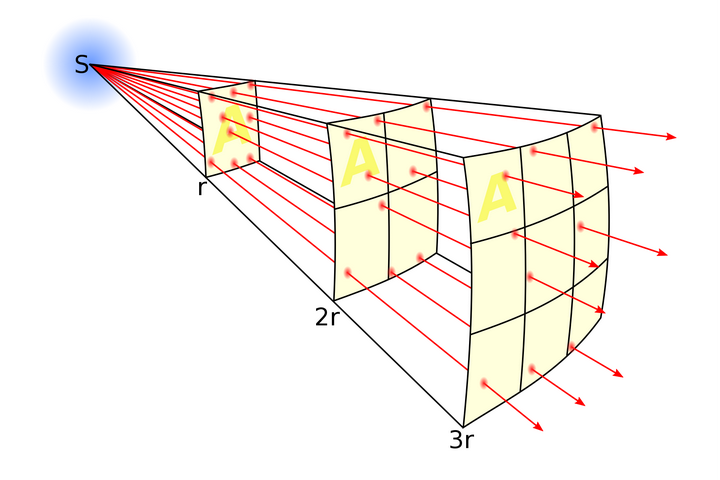
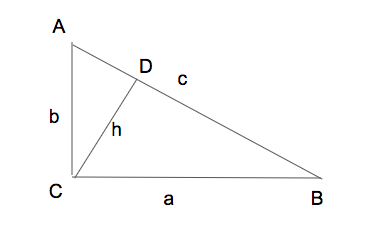
然后可以利用相似三角形的性质，即

$1/h^2=(1/a)^2+(1/b)^2$

将一个距离你

$h$

的点光源的强度转化成两个距离你分别

$a,b$

的点光源强度之和.

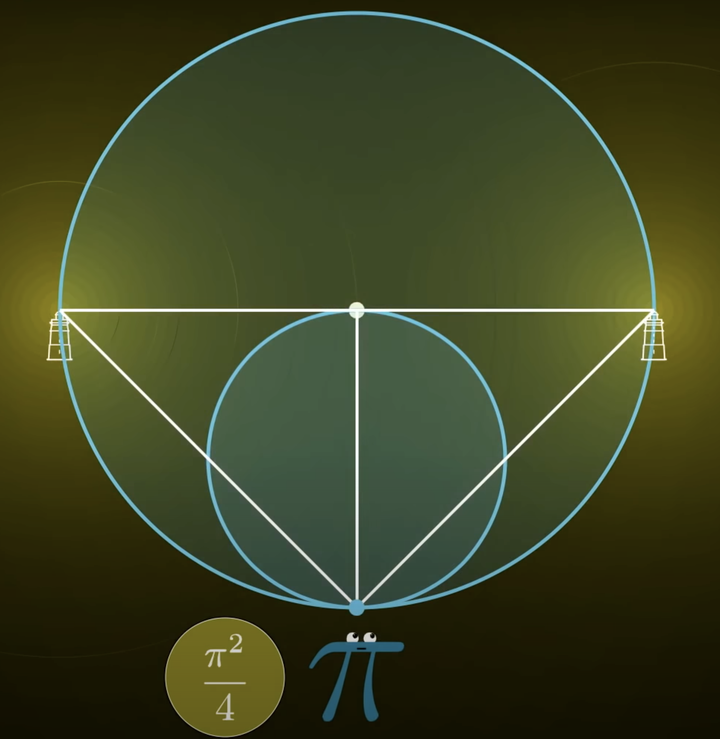
具体操作如下：考虑一个直径为

$2d$

的圆

$C_1$

，和原本的圆在你所在的位置

$O$

相切. 根据上面的相似三角形关系，可以将距离你

$d$

的点光源的强度替换成如下两个点光源

$A_1,A_2$

的强度之和. 由于对称性，这两个点光源和你的距离一样，不难验证

$\widehat{OA_1}=\widehat{OA_2}=1.$

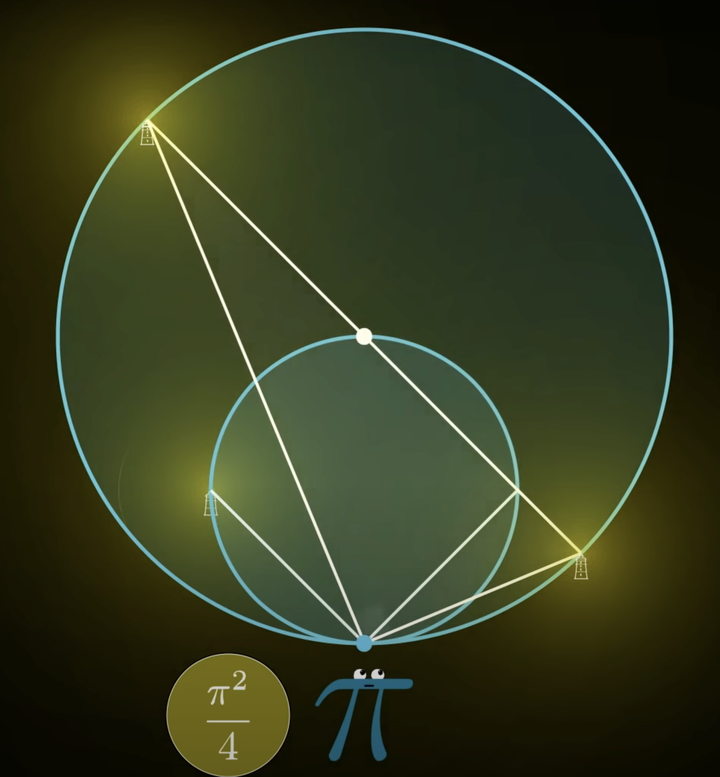
完成这一步之后，下一步做一个直径为

$4d$

的圆

$C_2$

，仍然与之前的所有圆在

$O$

点相切. 做一条

$C_2$

的直径过

$A_1$

，再把这条直径与

$C_2$

的两个交点分别和

$O$

连接，再次利用相似三角形将

$A_1$

转化成如图所示的两个点光源

$B_1,B_2.$

对

$A_2$

用相同的操作，这就把原本

$C_1$

上的两个点光源替换成了

$C_2$

上的四个点光源

$B_1,B_2,B_3,B_4.$

不难验证这四个点光源将圆

$C_2$

四等分。所以这四个点光源和你的距离(劣弧

$\widehat{B_i O}$

的长)分别为 1，1，3，3。

下一步，和第二步操作完全一样，现在做一个周长为

$6d$

的圆

$C_3$

，与所有圆在

$O$

点相切，对于每一个

$C_2$

上的点光源，做一条过这个点的

$C_3$

的直径，将直径与

$C_3$

的交点与

$O$

连接，利用相似三角形关系将这个点光源替换成

$C_3$

上的两个点光源。不难验证

$C_3$

上的 8 个点光源将这个圆八等分，与

$O$

形成的劣弧长度分别为 1，1，3，3，5，5，7，7.

继续重复这个步骤。于是在第

$n$

步，我们做一个直径为

$2nd$

的圆

$C_n$

，并且

$I=\pi^2/4$

是这

$2^n$

个点光源的强度之和，这

$2^n$

个点光源和

$O$

围成的劣弧长度分别为 1,1,3,3,5,5,7,7,9,9......当这个操作趋向于无穷的时候，圆越来越大，在你看来这个这些点光源就变成了一条直线上无限个间隔为 2 的点光源：

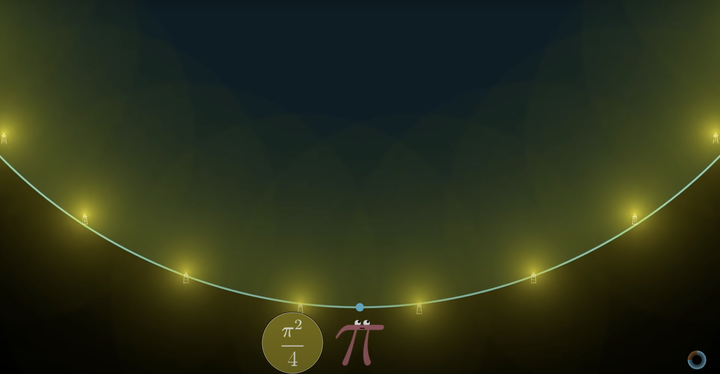
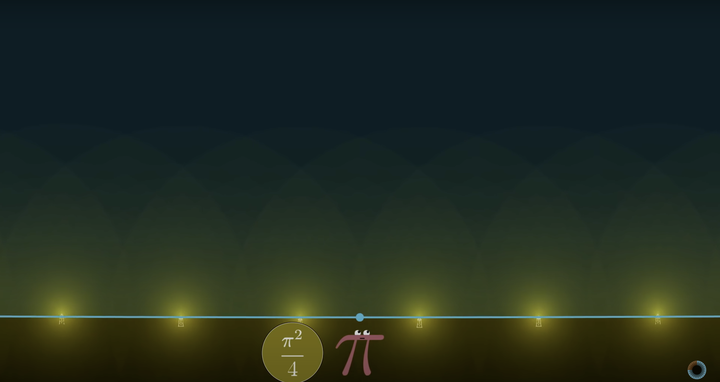
所以我们得到

$I=\frac{\pi^2}{4}=2\sum_{n=0}^\infty\frac{1}{(2n+1)^2}.$

对于偶数项，我们发现

$\sum_{n=1}^\infty \frac{1}{(2n)^2}=\frac{1}{2^2}\sum_{n=0}^\infty \frac{1}{n^2}.$

所以如果设

$S=\sum_{n=0}^\infty \frac{1}{n^2}，$

就有

$S=\sum_{n=1}^\infty \frac{1}{(2n+1)^2}+\sum_{n=0}^\infty\frac{1}{(2n)^2}=\frac{\pi^2}{8}+\frac{1}{4}S.$

解得

$S=\pi^2/6.$

微信扫一扫

微信扫一扫

有哪些知道了语源后会令人感到惊讶的英语单词？

上一篇

刻在人类基因中里的禁令有哪些？(刻在基因上的禁令)

下一篇

本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容，一经查实，本站将立刻删除。

网络百科

苹果手机各个功能介绍，iphone必须关闭的十个功能

1、关闭蓝牙。现在已经很少有人用蓝牙传输文件了，而且iPhone与安卓的蓝牙并不兼容，所以，可以在设置中，关闭蓝牙功能。2、关闭通知功能。关于APP推送，无非也就是一些更新提醒，关了也不会有什么影响，还能多省点电。3、关闭自动调节亮度功能。一般来说，可以将屏幕亮度在15%-30%之间，在强光环境中，在进行手动调整就可以了。4、禁止后台刷新。在设置—通用中，关闭后台自动刷新功能，也可以对省电起到一点...

2023-07-19 06:00:26
0
网络百科

高德打车怎么设置途经地，高德如何添加途经路线

1、点击高德地图APP界面底部的“导航”按钮，进入导航模式。2、点击右下角的“路线”，进入路线设定页面，根据要求输入起点、终点进行路线规划。3、点击“添加途经点”，弹出添加途经点页面，点击右上角，可以添加或者删除途经点，乘客可以手动输入要添加的途经点。4、当添加完途经点时，点击“确定”按钮，即可添加途经路线。此时地图会显示出这条路线上所有的途经点，以及当前途经点的地点信息。怎么设计高德地图设置要经...

2023-07-19 06:00:26
0
网络百科

高中必修二物理知识点总结，高一物理必修2重点知识点归纳

您好，1.运动学-位移、速度、加速度的概念及计算方法-相关运动的分析方法，如相对运动和抛体运动-牛顿运动定律及其应用2.力学-力的概念及种类，如重力、弹力、摩擦力等-牛顿第一、二、三定律及其应用-力的合成与分解-能量、功、动能定理、功率的概念及计算方法-动量、冲量定理及其应用3.热学-温度、热量、热能的概念及计量单位-热传递的方式及其特点，如传导、对流、辐射-热力学第一、二定律及其应用，如热机效率...

2023-07-19 06:00:26
0
网络百科

南北朝变态君主是如何养成的？(南北朝君主为什么很残忍)

建议还是不要拿审视宋以后（元除外）中国的视角看魏晋南北朝时期，宋以后中国的中央集权制才度基本完善，某些人口中的“秦制东方专制国”直到那个时间点才算是真正成型了，而这之前尤其是南北朝时期的政治逻辑和宋以...

2023-07-19 06:00:26
0
网络百科

石头互相摩擦为何产生白色?(什么石头遇水出现白色物质)

题主很细心，可以观察到这一现象，我来尝试解答一下这个问题，我来举一个比较极端的例子，比如黄铁矿，他是这个光泽和颜色地但是，当他在瓷片上划划痕的时候，划痕就变成了这个颜色矿物的这种性质，就成为了鉴定的一...

2023-07-19 06:00:26
0