简单说,这和黑洞的形成是同样的道理。
我们首先从宏观角度来看这个问题。之所以沸点下温度保持不变,是因为Gibbs 相律:
其中 F 是自由度,C 是系统组分数,P 是系统的相态数。对于汽 - 水系统,C=1,P=2,你自己算。
我们用水作为例子来说明。具体说,对于水蒸气,我们知道它的状态方程告诉我们,
对于孤立系统,它的质量不会发生变化,那么 PVT 三个变量,受到一个状态方程的约束,它就只有两个自由度,例如说,压力和温度。我们可以自由改变压力和温度,而密度随之改变。
但是,在沸腾的时候,有气液两相共存。
它有两相并存,于是每一相各自都有温度、密度、压力三个变量,整个体系而言,原本三个变量,现在变成了六个。我们多了三个变量,但是同时,也会多出来约束条件。我们可以数一下多出来的约束方程个数:
- 每一相都有自己的状态方程,于是原本一个状态方程,现在变成了两个。多出一个;
- 根据力学平衡条件:
,于是多出来第二个;
- 根据温度平衡(热力学第零定律),
于是,我们就多出来三个约束方程。
- 由于两相共存,两相之间会存在平衡关系,也就是热力学第二定律 - 两相的化学势相等,
,于是我们就有了第四个约束方程。
也就是说,我们多出来三个变量,但是却多出来四个约束方程。于是整个体系的自由度就少了一个。那么现在我们就只剩下一个自由度了。也就是说,只有一个变量就可以确定体系的状态了。当我们把压力固定(等压过程),它的温度自然就固定了。
我们可以看到,每多出一个相,就会少一个自由度。在压力一定的情况下,单纯的液体温度可以自由变化,但是,沸腾时多了一个相态,就少了一个自由度,温度就不能变化了。
简言之,由于两相之间各自不同的物理性质,而两相性质之间又有约束联系,最终导致了自由度少了一个。所以这个问题的关键,在于相变是一个不连续的过程:从液相到气相之间,存在一个两相并存的过程。在这个过程中,由于多了一个相,就少了一个自由度,所以等压条件下,就只能是等温的。简单用图示画出来,液相是这样的:
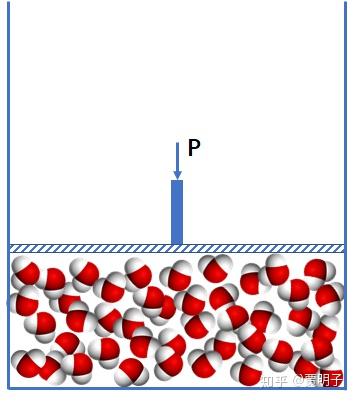
在不断加热的过程中,会出现两相共存:
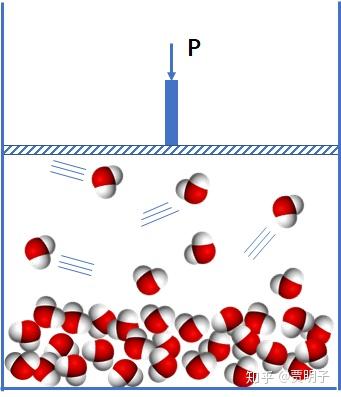
最终全部变成气相:
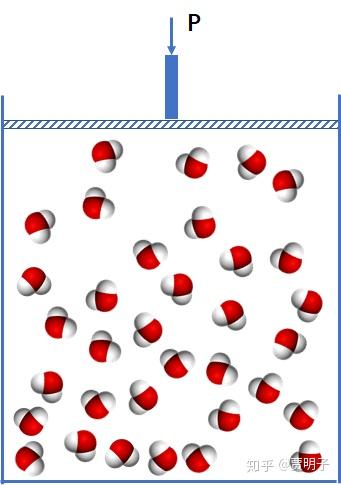
于是,你的这个问题,其实问的就是这个:
为何在完全液相变成完全气相的过程中,会出现两相并存,而不是渐变?
也就是说,从图 A 到图 C 的过程中,中间的过渡为何是图 B,而不是像下面图 B'这种情况(气液连续过渡):
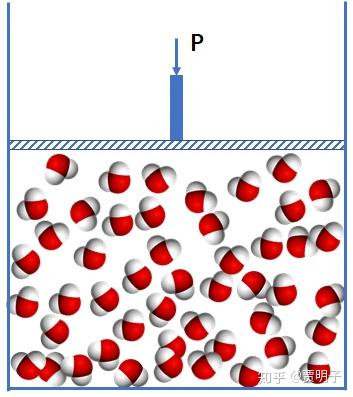
这个问题,可以简单地从分子间相互作用来解释。
我们知道,分子间力(范德华力)在分子靠得很近的时候,表现为斥力,这种斥力随着分子间的距离缩短而急剧上升。在分子间距离稍稍离开一点的时候,它表现为一种引力。这种引力会延伸一定距离并随着距离的增加连续减弱,而当分子达到一定距离之后,它会衰减为零。这个可以从下这张图表示:
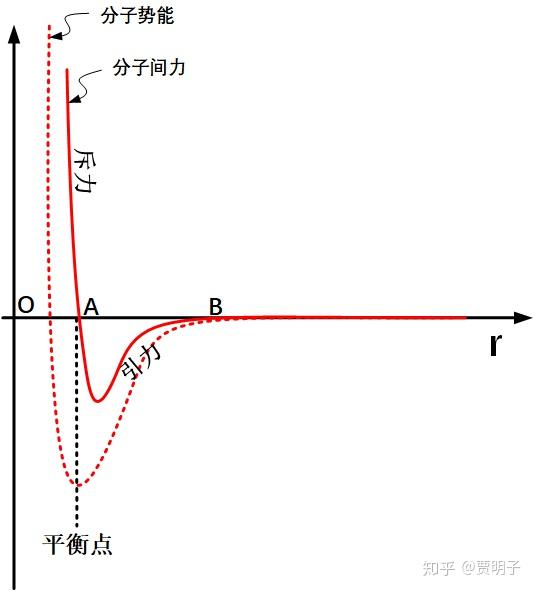
在这张图中,当分子间距离大于 B 时,分子间的相互作用就完全忽略,它们都是自由分子,互相之间只有碰撞,没有其他作用力 - 这也就是理想气体。
当分子间距位于 A 点时,分子间的引力和斥力达到平衡。从这一点远离,分子就会相互吸引,靠近就会相互排斥。于是这一点就形成一个势能低点(势阱),是无外力情况下的最稳定情况。在 AB 之间,分子表现为互相吸引。
我们可以想象一下一个系统,一开始处于气态(理想气体),在等压下,我们从其中抽取热量,会发生什么?
这个非常简单,抽取热量导致温度下降,在等压的条件下,气体体积逐渐缩小,密度变大,分子间距开始变小。在典型的气态下,分子间的距离大于 B 点,因此分子间只有相互碰撞,没有其他作用力。
我们暂时跳过相变过程 ,来看看当气体完全变为液体之后(分子间距大约在 A 点附近),我们持续向外抽取热量,它会如何?
这个也非常简单。在液态下,抽取热量,同样温度下降,但是此时它的体积却不会发明显变化(和气体相比)。随着热量的抽取,它的温度逐渐降低。
现在我们再来看从气态向液态转化的这段过程,会发生什么?为什么这个过程中会出现两相并存,而不是气体连续收缩,密度变大,直至完全变成液体 - 就像是图 B'所显示的那样?
我们假设气体的确是连续变成液体,而不是出现形成两相并存。那么,从 B 点开始,当我们继续抽取热量,气体体积继续缩小,会发生什么?
请注意,此时它的行为和就会和纯气体不同了,因为这时候分子之间有相互吸引作用。随着体积缩小,分子之间的吸引力变大,分子间的势能也会变低。这时,虽然总的能量变小了,但是,势能同样在下降,而往往,势能下降的比抽取的热量更多,那么,它的动能就会增加。我们知道,温度是分子动能的体现,那么此时温度就会上升。
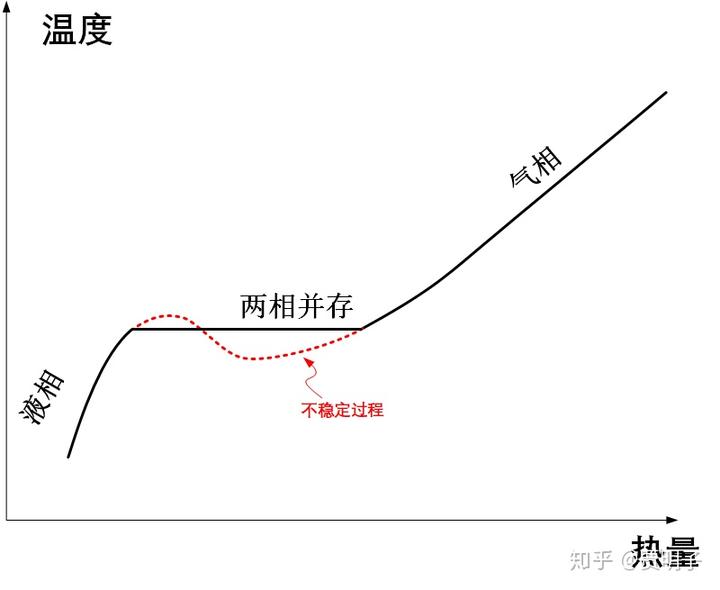
总而言之在分子间距在 AB 之间的时候,也就是说在气体密度足够大的时候,我们抽取热量,气体收缩的过程,就可能伴随着分子间吸引力做功的过程,这个功必然就转化为分子动能,导致温度反而上升。我们把整个过程用下图表示:
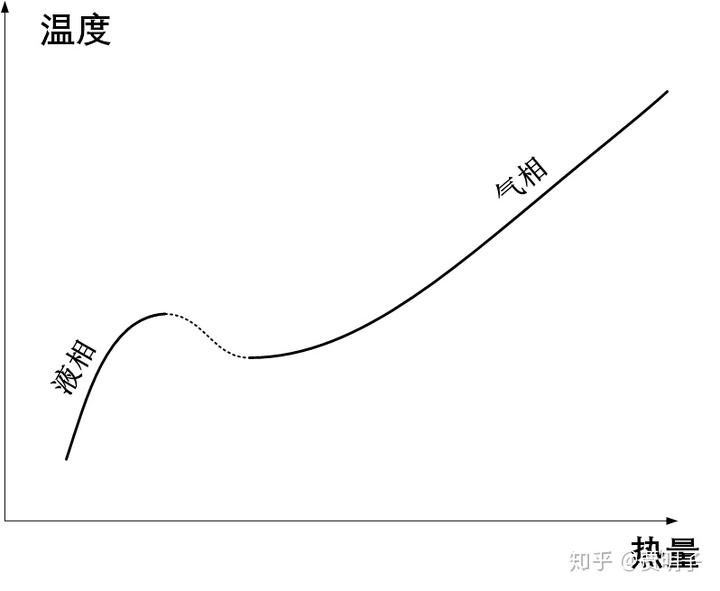
我们可以看到,在相态转化的过程中(图中的虚线部分),会出现这样一种怪异的过程:随着我们从系统抽取热量,它的温度会上升;反之亦然,如果我们加热它,它的温度不升反降。这是一个负热容的情形。
这就和黑洞的形成非常相似:我们知道,巨大的恒星在坍缩过程中,会表现出负热容。由于万有引力的存在,恒星就会不断坍缩:
- 万有引力导致恒星收缩;
- 收缩过程中引力做功导致温度上升;
- 温度向外辐射,分子动能下降,导致对引力的抵抗力下降;
- 恒星进一步收缩,密度增加,引力增强,导致收缩更加严重;
- 于是温度更加升高,向外放热更多;
- 最终恒星的收缩永远停不下来,直至变成黑洞。
这就是负热容系统表现出来的不稳定性:它不可能稳定地存在下来。
那么在我们面临的相变过程中,也是一样的:
- 分子间引力导致气体收缩;
- 收缩过程中引力做功导致温度上升;
- 热量向外散失,分子动能下降,对收缩的抵抗力下降;
- 气体更加收缩,密度增加,分子间距变小,引力更加增强,导致收缩更加严重;
- 于是温度更加升高,向外放热更多;
- 最终气体的收缩永远停不下来,直至变成液体。
当然,相变过程和黑洞形成还是有一点点不同的。因为随着分子间距的缩小,它的引力就会逐渐开始向着斥力转变,于是它最终就稳定下来,变成液体。所以我们不必担心它会停不下来最后直接变成黑洞。
于是乎,上面虚线的那一段过程,是一个仅仅在理论上存在,但是实际上不可能稳定存在的过程。也就是说,在图 B'表示的那种均匀的体系下,其中的一部分分子会迅速收缩到一起,变成液态。而在这一部分分子的收缩过程中,会放出热量,这些热量就导致它们周边的分子能量上升,结果就是上述过程的反过程:
- 分子能量上升,开始膨胀;
- 膨胀过程分子克服引力做功,导致温度下降;
- 温度下降会从周围吸收更多热量,能量更加上升;
- 分子间距增大,吸引力变小;
- 吸引力变小导致分子更加膨胀,直至引力消失,变成自由分子。
也就是说,这个不稳定状态,会迅速向着两侧坍塌:要么迅速变成气体,要么迅速变成液体,反正不可能以这种形态稳定存在。就好像是一个“山坡”顶部的球一样,它理论上可以平衡,但是实际上它不会呆在山顶,因为它要么滑向左侧,要么滑向右侧:
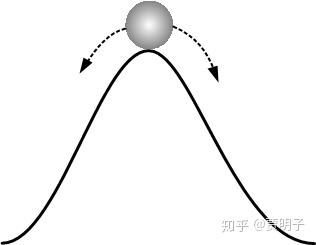
这个,就是数学上的鞍点,是一种典型的失稳情况。
所以说,图 B'点是一种理论上存在,但是实际中不存在的状态。实际气体内部总是存在着无休止的涨落的,B'的状态对这些涨落毫无抵抗能力。在气体内部总存在着不同涨落的区域,使得它像上面那个山顶的球一样,要么滑向左边(液态),要么滑向右边(气态)。于是就出现了气液两相并存的情况了。
值得注意的地方是,在气体内部任何一个局部区域的失稳,都将会导致其周围区域向着相反的方向失稳。就像是火药的药捻可以点燃整箱炸药一样,一个局部的“液滴”形成就最终就引发整箱气体的崩溃:在内部的任何一处,要么变成稳定的气态,要么变成稳定的液态。
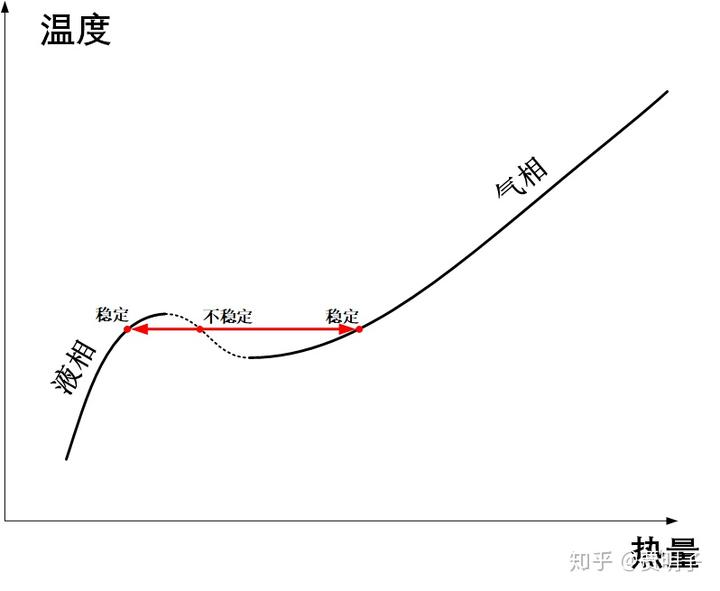
所以说,最终的相变过程,就是我们日常所熟悉的那种,在沸点处温度保持不变,两相并存,知道液体完全蒸发完毕的这种不连续变化。连续变化不是违反了什么物理定律,而是因为它不稳定:
关于负反馈的稳定性丧失,可以参考我的文章:
贾明子:9、我们这个反馈的世界
以及我的回答:
水在临界点发生了什么?
--------------
回应一下评论中的疑问吧。 @全力的一度狐@yahoc


这个问题就是,
- 是不是有时候,势能的下降不足以补偿抽取的热量?
- 如果这种情况存在,是不是就没有固定的相变点呢?
这两个答案都是肯定的。
是的,的确有某些条件下,势能的下降不足以补偿抽取的热量。在这个时候,无论我们从系统抽取多少热量,它总不会出现冷凝的现象。它会逐渐地降温,最终变成液态。这就是超临界现象。
我们可以先来看看,用水 - 水蒸气系统为例,随着我们抽取热量,在液化过程中它的温度变化(用 python 的量子化学模拟库 Psi4 计算,过程从略):
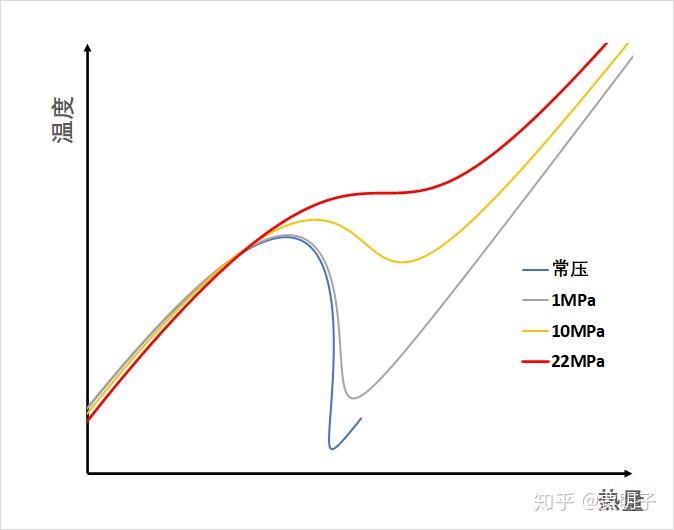
我们可以看到,随着系统的温度和压力增加,这种负热容的现象就越来越不明显。一直到压力达到 22MPa 的时候,负热容就不复存在。我们知道,负热容的消失,就意味着整个过程中它的状态都是稳定的,也就不存在突然崩溃成为气液两相的过程了。于是乎,随着热量的抽取,它会连续变化成为液态,这个 22MPa,就是水的临界压力。请参考:
水能否烧到一千摄氏度?
当系统处于液态向气态转化的过程中,是不是总是会产生不稳定的负热容状态呢?答案是否定的。
为何在超临界的情况下,就不会出现失稳现象呢?非常粗略地讲,气体一直处于一种受力平衡下:
外界的压力=分子碰撞力 - 分子间吸引力
当分子间距很远(比较稀薄)的时候,分子间力约等于零,此时外界压力就等于分子对容器壁的碰撞。我们知道,这是理想气体;
当气体密度比较大,分子间距足够近的时候,分子间的吸引力就起作用了。如果此时分子间的碰撞比较小,那么吸引力就起到关键作用,分子势能就会非常显著。正是这种势能导致了气体在向外散热时温度反而上升的怪异情形。这就是前面所说的两相并存。
但是,如果分子的运动非常剧烈(温度和压力很高),那么此时的主导仍然是分子间的碰撞,分子间的吸引力就不再明显。于是乎就起不到关键作用。系统就连续变化了。
谢谢 @天上的果子 在评论区的提醒,所以把它延伸到超临界情况。

 微信扫一扫
微信扫一扫 



