两个条件。1 - 易于理解, 2 - 未解
1 - 考拉兹猜想,又叫 3n+1 猜想,角谷猜想
取正整数,如果奇数则乘以 3 加 1,如果偶数则除以 2,那么经过有限步必然进入 4 -> 2 -> 1 -> 4 ...的循环。
直至 2017,所有
以下的正整数都经过机器验算,但还没有人能证明或举出反例。
鼎鼎大名的保罗·厄多斯曾表示“也许数学还没准备好解答这类问题。”2010 年,美国数学家 Jeffrey Lagarias 表示这是个“极端困难的问题,完全超出今天的数学所能解决的范围。”
2 - 移动沙发问题
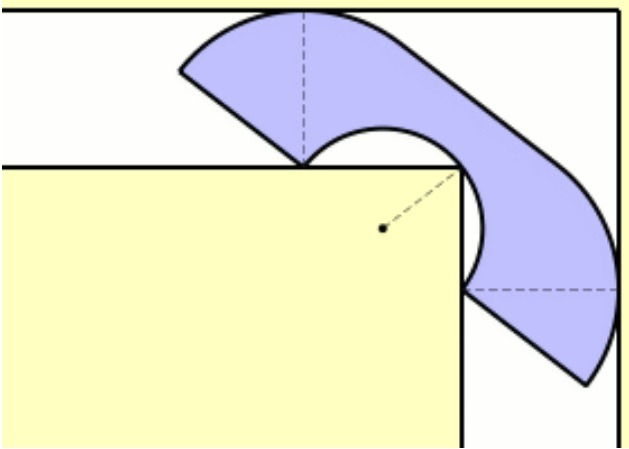
假设有 L 形的转角走廊,走廊宽度为 1,那么面积最大多大的形状可以转过转角?
这一问题的答案被称为沙发常数,目前还未找到。
下图是英国数学家 John Hammersley 发明的形状,由两个四分之一圆 + 矩形 - 半圆组成,面积约为 2.2074。
之后美国数学家 Joseph Gerver 构筑了由 18 段曲线拼接成的形状,将沙发常数的下限抬高到 2.2195。
2017 年的一份论文将沙发常数的上限大大减少,证明了该数不可能超过 2.37。
3 - 内接正方形问题
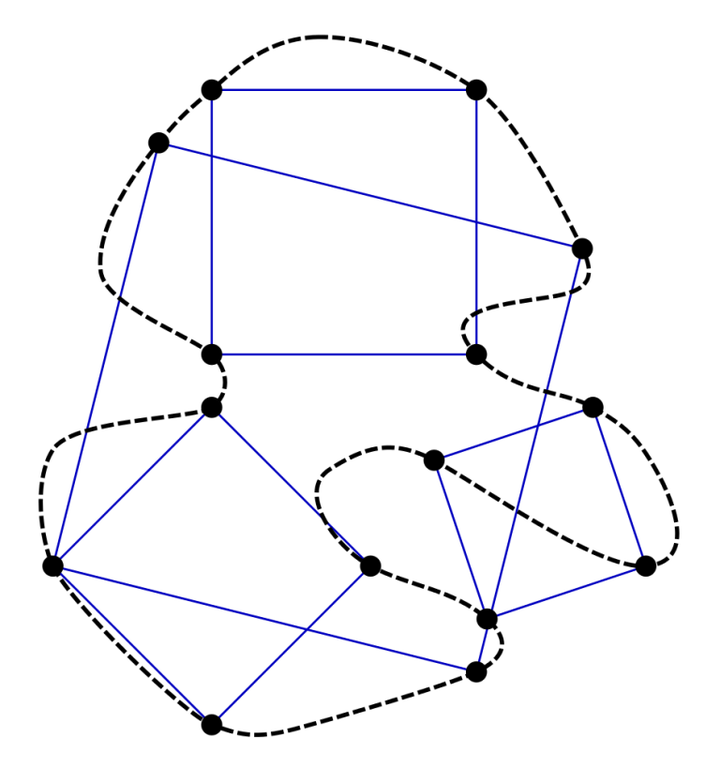
画一条简单封闭曲线,形状不限,只要满足起点和终点重合,曲线不和自身相交两个条件,则一定可以找到一个正方形,四个顶点都位于该曲线上。
类似定理对于三角形和长方形都已经证明,但正方形的难度更上一级。
目前成功证明了这一猜想对于满足一些额外条件的曲线成立。如曲线为分段解析等等。

 微信扫一扫
微信扫一扫 



