嗯,好问题!
我们从根源来介绍一下范畴论!
以前为了描写对称性,群论走进了物理。现在为了描写量子材料中的量子纠缠,范畴论也正在走进物理。可到底什么是范畴论?
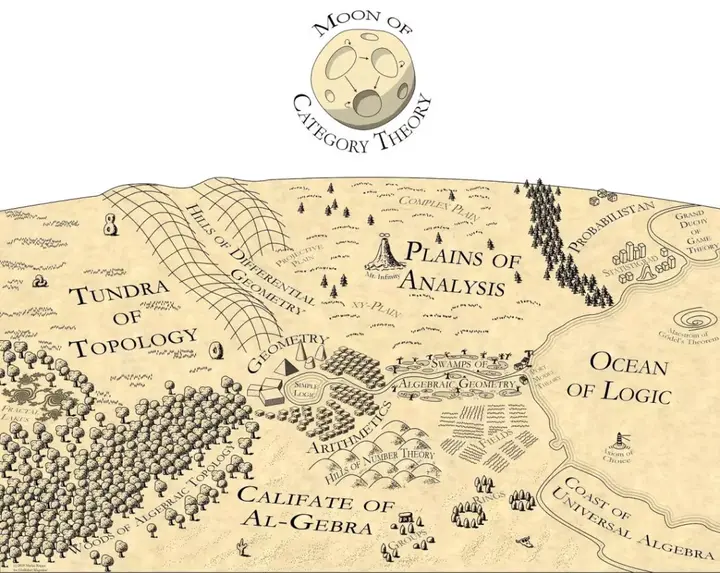
范畴论是一个关于关系的理论,描述并研究关系的所有可能性质。如果绘制一幅数学地图,地面上会有代数、拓扑、分析等不同领域,而范畴论则像是悬挂在天空中的月亮,它提供整个地图的缩略图,让我们看到在地面看不到的各个领域之间的关系,证明看似不相关的数学领域并非完全不同。当你在某个数学领域的边界处艰难跋涉时,范畴思维可以指引你,它增强你的直觉,让你的洞察力更敏锐。而这一关于关系的全面抽象理论,也正好是描写多体量子纠缠的自然语言。
撰文 | Tai-Danae Bradley
译者 | 唐璐

从最早开始学习数学,我们就知道代数与几何有很强的关联,代数方程可以表示成图形和几何对象,几何特征可以用代数表达式刻画。就好像有一座桥梁连接广阔的数学世界中的这两个领域,桥的两边互为镜像。
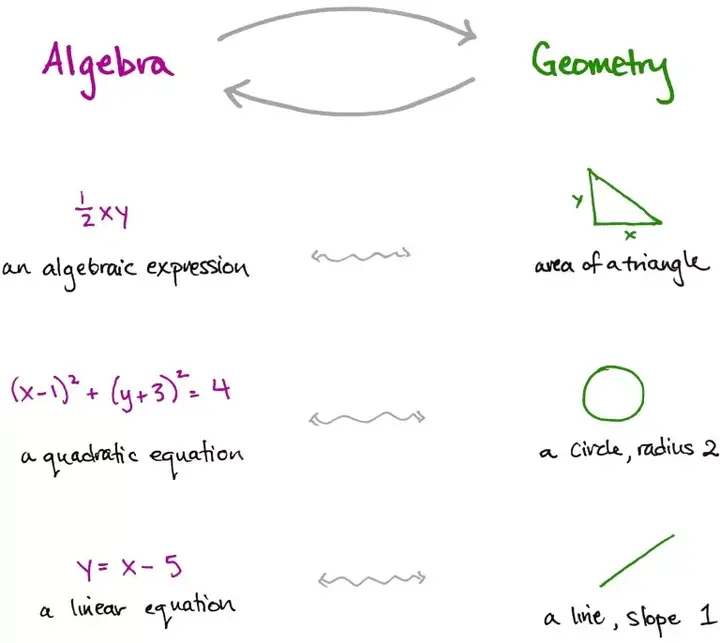
代数与几何之间对应关系的 3 个例子:代数表达式 - 三角形面积,二次方程 - 半径为 2 的圆,线性方程 - 斜率为 1 的直线。
因此,尽管代数和几何是很不相同的数学领域,但这种联系表明,它们之间存在着内在关联。不仅如此,还有集合论、群论、线性代数、拓扑学、图论、微分几何等等,这些看上去似乎没什么关系的数学分支实际上都存在深层次的关联,代数与几何的关联只不过是其中的冰山一角。令人惊奇的是,这些关联或桥梁不仅仅是浮于表面的印象。它们是数学,而且这种数学有个名字:范畴论。
范畴论是什么?
马丁·库佩(Martin Kuppe)曾绘制过一幅精美的数学地图,其中范畴论高高悬挂在天空,提供了整个地图的缩略图。它让我们能够看到在地面看不到的各个领域之间的关系,证明看似不相关的数学领域并不是完全不同。当你想解决某个领域(比如说拓扑)中的问题,但没有合适的工具可以使用时,这就变得非常有用。通过将问题转移到不同领域(比如群论),就能让你换个角度看问题,说不定还能发现新的工具,让问题变得更容易解决。事实上,范畴论就是这样产生的。它诞生于 20 世纪 40 年代,背景是人们试图用更简单的代数方法来解决一个困难的拓扑问题。
回到数学地图,你可以注意到各领域都包含一些对象:集合论有集合,群论有群,拓扑学有拓扑空间...... 这些对象彼此关联:集合通过映射关联,群通过同态关联,拓扑空间通过连续映射关联......
这条共同的线索贯穿了整个地图,将各领域统一到一起。范畴论将这种统一形式化了。更具体地说,范畴是一组对象及其关系的集合,这些对象之间的关系(称为态射,morphisms)在组合(composition )和结合性(associativity)方面表现良好。这样就为数学提供了一个模板,将不同内容输入模板,就能重建一个数学领域:集合范畴由集合和它们之间的关系(映射)组成;群范畴由群和它们之间的关系(群同态)组成;拓扑空间范畴由拓扑空间和它们之间的关系(连续映射)组成;等等。

集合与集合之间的关系(映射);群与群之间的关系(群同态);拓扑空间与拓扑空间之间的关系(连续映射)。
巴里·马祖尔(Barry Mazur)写了一篇精彩的非专业性文章介绍范畴论,《什么时候一样东西等于另一样东西?》,范畴和模板的类比就是在这篇文章中提出来的。他在文中写道:“范畴的概念是万能的......几乎没有哪种数学对象不适合这个方便并且经常能带来启发的模板。” 事实上,正如范畴论专家尤金妮娅·程(Eugenia Cheng)在她的论文《高维范畴论》中所指出的,“范畴论是数学的数学。”
关系就是一切
范畴论的一个主要特点是它剥离了很多细节:它并不具体关心集合中的某个元素,或者某个群是否可解,或者某个拓扑空间是否有可列基。所以你可能会想,“呃,范畴论似乎太抽象了。这样做有什么好处吗? ” 当然,答案是肯定的!剥离细节的一个好处是,我们的注意力从单个对象上转移开,转向它们之间存在的关系——态射。任何一个范畴论专家都会告诉你:关系就是一切。

事实上,范畴论的一个主要信条就是,一个数学对象完全由它与所有其他对象的关系决定。换句话说,当且仅当两个对象以同样方式与范畴中的每个对象相关时,两个对象本质上是不可区分的。这其中的主旨 [这是著名的米田引理(Yoneda lemma)的一个推论] 与我们的日常经验并没有太大区别。你可以通过观察人们的关系来了解他们,比如他们在 Facebook 上的朋友,他们在 Twitter 上关注的人,他们周五晚上和谁出去玩。如果你遇到两个人,他们有完全相同的朋友,他们在社交媒体上的互动也完全相同,他们在周五晚上和相同的人在一起,那么你可能会开玩笑地说,“你甚至分不清他们。”撇开所有玩笑不谈,范畴论告诉我们,这其实是真正的数学!
那你可能会想,“嗯,如果数学关系如此重要,那么范畴之间的关系呢?它们存在吗? ”问得好。答案是:当然!事实上,这些特殊的关系有个名字——函子(functor)。但是为什么要就此止步呢?这些关系之间的关系呢?它们也有名字:自然变换(natural transformation)。
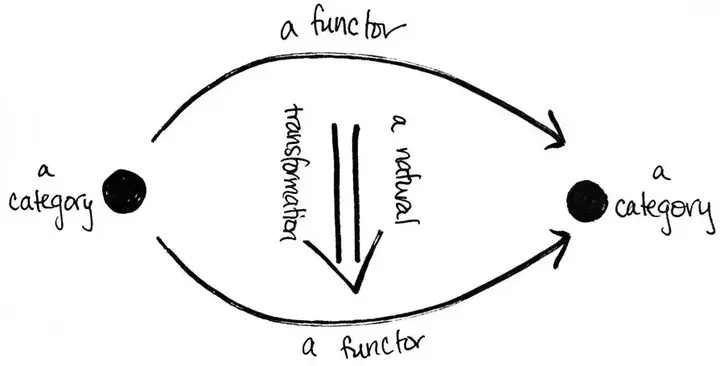
范畴之间的关系被称为函子,函子之间的关系被称为自然变换。
事实上,我们可以继续:“关系之间的关系之间的关系......?”这样做将使我们进入更高维的范畴论,这正是尤金妮娅·程的主要研究领域。
尽管听起来很抽象,但这些构造——范畴、函子和自然变换——组成了一个理论宝库,不仅仅涉及数学,还涵盖许多学科!范畴论自诞生以来,已经在计算机科学、量子物理学、系统生物学、化学、动力系统和自然语言处理等领域找到了自然应用。(“应用范畴论”网站上有一个应用列表,http://appliedcategorytheory.org/workshops) 因此,虽然范畴论听起来有点抽象,它其实具有很多实际应用。这并不奇怪。范畴论是关于关系的,而关系在我们所处的世界中无处不在!
结 语
范畴有点像凤尾鱼:有些人天生喜欢,而对其他人则是一种后天习得的口味。所以是的,范畴论确实不能在求极限时为你的 ε 找到一个 ,或者确定你的 520 阶的群是否为单群,或者为你的偏微分方程构造一个解。为了做到这些,我们必须脚踏实地。但是,当你在最喜欢的数学领域的角落和缝隙中艰难跋涉时,范畴思维可以指引你——它可以增强你的直觉,让你的洞察力更敏锐。如今,我们尤其难以摆脱范畴论在现代数学中的普遍存在。所以无论你学数学的目标是什么,学习一点关于范畴的知识都是值得的!
作者介绍
Tai-Danae Bradley是纽约城市大学数学博士生。感兴趣的领域包括范畴论、拓扑学、机器学习和量子物理,空闲时间爱好涂鸦和写博客。
本文翻译自http://chalkdustmagazine.com,原文标题为“An invitation to category theory”

 微信扫一扫
微信扫一扫 



