哈密顿原理和拉格朗日函数的由来是怎样的？_网络百科

逻辑上，哈密顿原理可以推出拉格朗日方程。但人们的认知过程是：先得出拉格朗日方程，再根据方程的形式总结出更基本的哈密顿原理。

先来看两个问题和两个方程。

第一个问题是约束力问题：如何消去牛顿运动方程中难以求解的约束力？

拉格朗日给出了答案：只要选取相互独立的广义坐标

$q_\alpha, q_\beta...$

, 用它们去替代原有的笛卡尔坐标

$x,y...$

, 就可以消去约束力和约束方程，让一组相互耦合的牛顿运动方程变成更简洁的相互独立的形式。代换后得到的方程就是拉格朗日方程：

$\frac{d}{dt} \left(\frac{\partial{L}}{\partial{\dot{q}_\alpha}} \right)-\frac{\partial{L}}{\partial{q_\alpha}}=0$

其中

$L=T-V$

, 是体系的动能与势能的差，称为拉格朗日量。

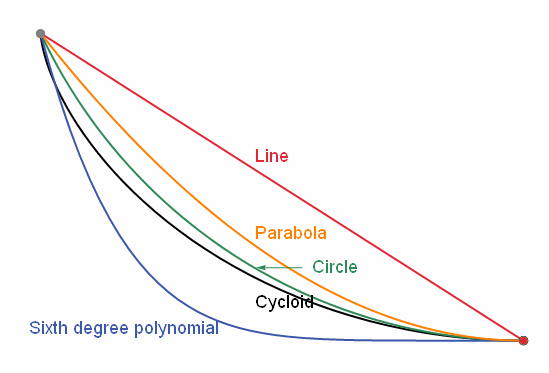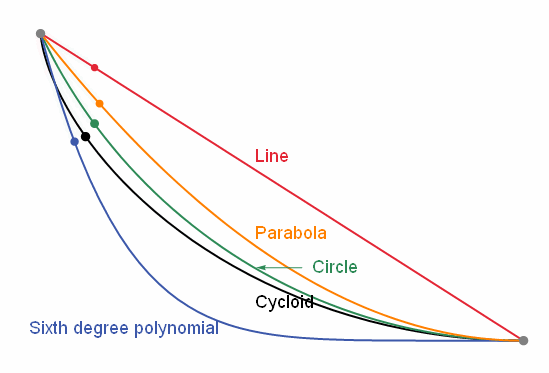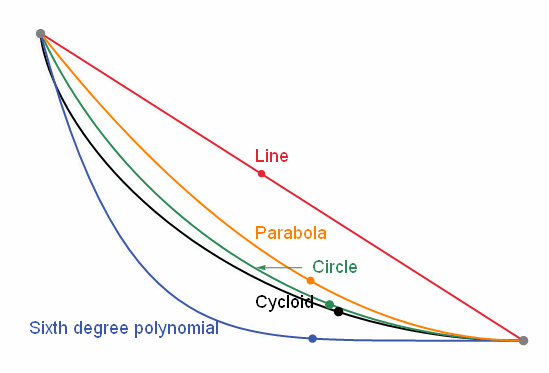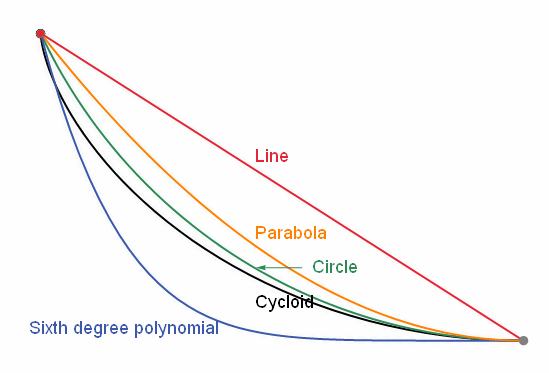
第二个问题是“最速降线”问题：一个小球在只受重力、不计摩擦的情况下，从一点 A, 以何种曲线运动到不高于 A 的 B 点，使整个过程所需的时间最短？

这个问题可以抽象成纯数学问题：当积分

$J=\int_{x_1}^{x_2}F(x,y,y')dx$

取极值时，函数

$y(x)$

应具有何种形式？

欧拉用变分法给出了这个问题的答案，这个条件下的函数

$y(x)$

应满足欧拉方程：

$\frac{d}{dx} \left(\frac{\partial{F}}{\partial{y'}} \right)-\frac{\partial{F}}{\partial{y}}=0$

这两个方程是不同的人，在不同的时代，为解决完全不同的问题，而推出的具有完全不同意义的两个方程。但很明显，两个方程具有一模一样的数学形式。

这是巧合吗？

是的。

基于这一巧合，哈密顿提出：既然满足欧拉方程的函数

$y(x)$

使积分

$J=\int_{x_1}^{x_2}F(x,y,y')dx$

取极值，那么对应拉格朗日方程，也一定有积分

$S=\int_{t_1}^{t_2}L(t,q_\alpha,\dot q_\alpha)dt$

取极值。这个拉氏量在时间上的积分就是哈密顿作用量。上面分析说明：力学体系从时刻

$t_1$

到时刻

$t_2$

的一切可能运动之中，只有使哈密顿作用量取极值的运动，才是实际发生的运动。这就是哈密顿原理。从哈密顿原理可以推出拉格朗日方程，但发现的时间，却是拉式方程在先，哈氏原理在后。

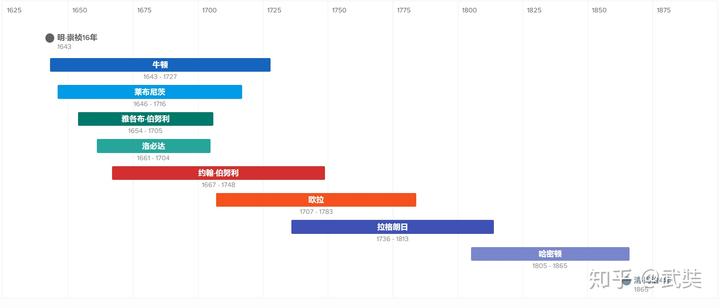
捋一下时间轴：1686 年，牛顿《自然哲学的数学原理》出版，提出三定律，经典力学体系初步建成。1728 年，欧拉用变分法求解最速降线问题，得到欧拉方程。1788 年，拉格朗日完成《分析力学》，提出拉格朗日方程。1843 年，哈密顿基于欧拉方程和拉格朗日方程的极度相似，提出了哈密顿原理。

顺便看看同时代的中国：1686 年，康熙爷与沙俄鏖战雅克萨，次年签订中俄《尼布楚条约》。1725 年，雍正爷正全国推行“摊丁入亩”和“火耗归公”。1792 年，乾隆爷正志得意满地撰写他的《十全武功记》。1842 年，道光爷签订中英《南京条约》。

整体逻辑如上，那么拉格朗日方程和欧拉方程又分别是怎样得到的呢？

先看拉格朗日方程。

其实靠牛顿三定律，再加上具体的力的形式（比如万有引力定律），就可以列出质点运动方程：

$F(\vec{r})=m\ddot{\vec{r}}$

在笛卡尔坐标下分解为三个方向的三个微分方程：

$\begin{cases} F_x=m\ddot{x}\\ F_y=m\ddot{y}\\ F_z=m\ddot{z} \end{cases}$

靠这个方程原则上已经可以解出质点的坐标和速度随时间的演化，经典力学体系已经完备。

但实际遇到的力学问题千奇百怪，大部分问题光靠牛顿运动方程是难以准确求解的。解牛顿运动方程面临的最大问题就是约束。比如单摆。小球本应在空间中做自由落体运动，但现在用绳子把它拴在固定点 O 上，小球就只能在以 O 为圆心，以摆长为半径的圆弧轨道上运动。这就是约束。绳子施加给小球，让它保持在轨道上不逃走的张力，就是约束力。和重力不同，这个约束力是未知的。

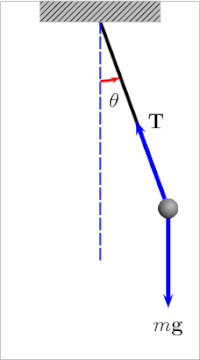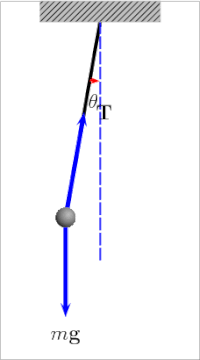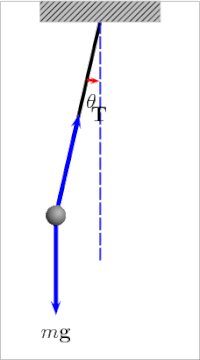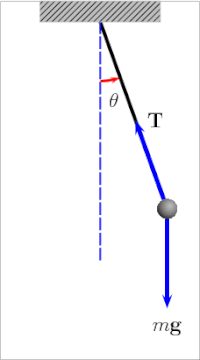
但列牛顿运动方程要求写出所有的力：

$\vec T+\vec G =m \ddot{\vec r}$

按笛卡尔坐标分解：

$\begin{cases} T_x=m\ddot{x}\\ \\ T_y-mg=m\ddot{y}\\ \end{cases}$

由于引入了额外的未知量——约束力，方程无法求解。这就是约束带来的最大问题。不过别忘了，我们还有已知条件没有利用，那就是约束方程。由于被绳子约束，小球的两个坐标并不独立，它们满足：

$x^2+y^2=l^2$

所以

$\begin{cases} T\frac{-x}{\sqrt{x^2+y^2}}=m\ddot{x}\\\\ T\frac{y}{\sqrt{x^2+y^2}}-mg=m\ddot{y}\\\\ x^2+y^2=l^2 \end{cases}$

三个方程，三个未知量，原则上可解。所以，含有约束的问题，如果要用牛顿运动方程求解，就必须引入未知的约束力，并同时引入和约束力数量相等的约束方程，使方程组可解。不过这样一来就同时增加了未知量和方程的数量。并且由于坐标不独立，各方向的微分方程相互耦合，极难求解。

拉格朗日给出了全新的解法。他的思路是：虽然约束力很复杂，但是大部分情况我们想知道的只是质点的运动情况，而不是约束力，那么能不能绕开约束力直接求解质点的运动？

答案是肯定的。

约束的实质是降维。绳子把二维平面中运动的小球限制在了一条一维的圆弧上。如果没有绳子，小球在水平和竖直两个方向上的坐标

$x,y$

相互独立，自由度是 2. 有了绳的约束，两个个坐标只要任意给定一个，则另外一个也随之确定，自由度是 1. 所以，只要用一个坐标，就可以确定小球的位置。这个坐标可以是

$x,y$

中的一个，也可以是一个新的参数。这个用以确定小球位置的参数，就是广义坐标。在这个例子里，选择绳和竖直方向的夹角

$\theta$

为广义坐标是方便的。准确地说，应该是选

$\theta$

和

$r$

为广义坐标，它们分别表示圆弧轨道的切向和径向。只是这里由于绳子的存在，径向的广义坐标

$r$

永远不变。所以只研究表示切向运动的

$\theta$

就可以了。这样，通过坐标变换，就把一个由两个不独立的坐标描述的问题，变成了用一个独立坐标描述的问题。

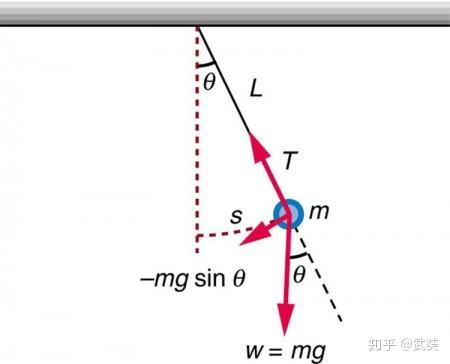
而且，这样选择广义坐标后，就会发现，约束力

$\vec T$

永远沿径向，而切向分量永远为零。于是在我们关心的切向的运动方程里，将不会出现约束力！切向的受力只有重力的一个分量，于是方程为：

$mg \sin\theta=m\dot{v}_\bot=ml\ddot{\theta}$

如果

$\theta$

足够小，方程可化为：

$mg\theta=ml\ddot{\theta}$

这和一维线性谐振子的运动方程一模一样，解是正弦函数。这是后话。

这样，就可以把前面那相互耦合的的 2 个微分方程 +1 个约束方程=总共 3 个方程，转化为仅仅 1 个独立的微分方程。

所以说，解一个有约束的力学问题，有两种方法：牛顿方法和拉格朗日方法。牛顿方法的思路是：引入 n 个未知的约束力，为保证方程可解，同时增加 n 个约束方程。拉格朗日方法则截然相反，通过选取恰当的广义坐标，直接消去所有的约束力和约束方程。

这样，面对诸如“套在环上的小环”，“一个端点固定的杆”，“被束缚在轨道上的过山车”等等这样有约束的力学问题时，就总可以用拉格朗日的思路，找到合适的广义坐标，避开约束力去列出独立精简的运动方程了。

就这么简单？

远不是。

“剑一人敌，不足学，学万人敌。”

项羽当年嫌剑法只能一对一打斗，没意思，闹着要学能万人敌的兵法。

诚然我们可以根据刚才拉格朗日的思路，在各个实际的具体问题中找到合适的方向和坐标，把约束力和约束方程避开，列出运动方程。正如用一把剑，把敌人一个一个地杀死。

但拉格朗日和楚霸王同样心高气傲。他岂能满足于“具体问题具体分析”的雕虫小技？他要开宗立派，他要把这种思想升华为普适的，能一劳永逸地解决一切力学问题的根本性方法！

他做到了。1788 年，巨著《分析力学》出版。在这部书中没有一幅插图，完全用数学分析的方法来解决所有力学问题，和牛顿的《自然哲学的数学原理》中比比皆是的几何分析形成刺目的对比。“四大力学”之首的理论力学由此奠基。拉氏从此封神。

那个能一劳永逸地解决所有问题的法门，就是拉格朗日方程：

$\frac{d}{dt} \left(\frac{\partial{L}}{\partial{\dot{q}_\alpha}} \right)-\frac{\partial{L}}{\partial{q_\alpha}}=0$

其中

$L=T-V$

, 是体系的动能与势能的差，称为拉格朗日量。

$q_\alpha$

是选取的广义坐标。它对时间的导数就是广义速度。

刚才单摆的例子中，

$q_\alpha=\theta$

, 动能和势能分别为：

$T=\frac12mv^2=\frac12ml^2\dot\theta^2$

$V=mgl(1-\cos\theta)$

（以最低点为零势能点）

拉氏量：

$L=T-V=\frac12ml^2\dot\theta^2-mgl(1-\cos\theta)$

代入拉式方程得：

$\frac{d}{dt} \left(ml^2\dot\theta\right)-mgl\sin\theta=0$

即

$ml^2\ddot\theta-mgl\sin\theta=0$

和上一部分得到的方程一模一样（多乘了一个

$l$

, 可理解为力矩和角动量的变化）。

这就是“万人敌”的拉格朗日方程。把动能和势能用广义坐标表示出之后，丢进去，直接输出想要的独立微分方程。

那么这个方程是怎样得到的？

对于一个运动的质点，我们的出发点是牛顿运动方程：

$\vec{F}+\vec{R}=m\ddot{\vec{r}}$

其中，力被分成了主动力

$\vec{F}$

和约束力

$\vec{R}$

两部分。上式也可以写成：

$\vec{F}+\vec{R}-m\ddot{\vec{r}}=0$

现在希望消去约束力，应该怎么办？

这就要用到一个性质：约束力不做功。原因是质点如果被约束在一条轨道，或一个曲面上时，约束力总是和这个轨道或曲面垂直，从而从不做功。这样，设想如果质点在这个轨道或曲面内发生一个小位移

$\delta \vec r$

, 必有

$\vec{R}\cdot\delta \vec r=0$

. 于是在牛顿运动方程两边乘上

$\delta \vec r$

, 即可消去约束力：

$(\vec{F}-m\ddot{\vec{r}})\cdot\delta \vec r=0$

这就是达朗贝尔原理。注意刚刚乘的小位移

$\delta \vec r$

并不是任意的，而是要在约束允许的范围内。它也有个专门的名字，叫虚位移。把上式在笛卡尔坐标下展开：

$(F_x-m\ddot{x})\cdot\delta x+(F_y-m\ddot{y})\cdot\delta y+(F_z-m\ddot{z})\cdot\delta z=0$

把

$x,y,z$

记作

$x_1,x_2,x_3$

. 可以把上式写成紧凑的形式：

$\sum_{i}^{}{(F_i-m\ddot{x_i})\cdot\delta x_i}=0$

由于约束的存在，虚位移的三个分量是不独立的。他们的关系由约束方程决定。如果约束是一个曲面，则有一个约束方程。如果约束是一条曲线，则有两个约束方程。如果不存在约束，则三个方向的虚位移独立，可任意取值。这时运动方程就退化回牛顿形式。

假设约束后的物体自由度是 2，则可选取 2 个独立的广义坐标

$q_1, q_2$

取代

$x_1, x_2,x_3$

来描述位置：

$\begin{cases} x_1=x_1(q_1,q_2)\\\\ x_2=x_2(q_1,q_2)\\ \\x_3=x_3(q_1,q_2)\\ \end{cases}$

所以，虚位移可表示为：

$\delta x_1=\frac{\partial x_1}{\partial q_1}\delta q_1+\frac{\partial x_1}{\partial q_2}\delta q_2$

一般地，有：

$\delta x_i=\sum_\alpha {\frac{\partial x_i}{\partial q_\alpha}\delta q_\alpha}$

把它代入达朗贝尔原理等式，就可以把笛卡尔坐标替换为广义坐标：

$\sum_{i}{\sum_\alpha{(F_i-m\ddot{x_i}) \cdot{\frac{\partial x_i}{\partial q_\alpha}}} \delta q_\alpha}=0$

求和次序可交换：

$\sum_{\alpha}{\left( \sum_i{(F_i-m\ddot{x_i}){\frac{\partial x_i}{\partial q_\alpha}}} \right) \cdot \delta q_\alpha}=0$

由于各个

$\delta q_\alpha$

独立自由，可任意变化，于是每个

$\delta q_\alpha$

前面的乘数必须为零：

$\sum_i{(F_i-m\ddot{x_i}){\frac{\partial x_i}{\partial q_\alpha}}} =0$

到了这里，就把按笛卡尔坐标三个分量方向划分的相互耦合的方程，转换为沿广义坐标方向的独立方程。但是还没完，我们还需要把方程里残留的笛卡尔坐标

$x_i$

都消掉，变成彻底由广义坐标表示的方程。

方程左边由两项构成，第一项简单：

$Q_\alpha =\sum_i{F_i{\frac{\partial x_i}{\partial q_\alpha}}}$

它表示力在广义坐标

$q_\alpha$

方向上的分量，叫做广义力。如果质点受到的力为保守力，则广义力还可以表示为势能的函数：

$Q_\alpha =\sum_i{-\frac{\partial V}{\partial x_i}{\frac{\partial x_i}{\partial q_\alpha}}} =-\frac{\partial V}{\partial q_\alpha}$

第二项比较棘手：

$P_\alpha= \sum_i{m\ddot{x_i}{\frac{\partial x_i}{\partial q_\alpha}}}$

怎样消去其中的

$\ddot x_i$

利用分部求导法则，可以先把二阶导数降为一阶导数：

$m\ddot{x_i}{\frac{\partial x_i}{\partial q_\alpha}}= \frac{d}{dt} \left( m\dot{x_i}{\frac{\partial x_i}{\partial q_\alpha}}\right)- m\dot{x_i}\frac{d}{dt} \left( \frac{\partial x_i}{\partial q_\alpha} \right)$

可以看出，

$m\dot{x}_i=mv_i$

其实就是动量在某个方向的分量，它等于动能对速度的导数：

$\frac{\partial T}{\partial \dot{x}_i}= \frac{\partial (\frac12 m\dot x_i^2)}{\partial \dot{x}_i}=m\dot{x}_i$

这样前面的式子就变成：

$m\ddot{x_i}{\frac{\partial x_i}{\partial q_\alpha}}= \frac{d}{dt} \left( \frac{\partial T}{\partial \dot{x}_i}{\frac{\partial x_i}{\partial q_\alpha}}\right)- \frac{\partial T}{\partial \dot{x}_i}\frac{d}{dt} \left( \frac{\partial x_i}{\partial q_\alpha} \right)$

离成功越来越近了，可惜还差一点。我们希望可以消去中间变量

$x_i$

而把式子全部表示成动能

$T$

和广义坐标

$q_\alpha$

之间的关系。令人欣慰的是，确实可以做到这一点。

首先，由复合函数求导法则，有：

$\dot x_i=\sum_{\alpha}{\frac{\partial x_i}{\partial q_\alpha}\frac{dq_\alpha}{dt} }=\sum_{\alpha}{\frac{\partial x_i}{\partial q_\alpha}\dot q_\alpha}$

两边对

$\dot q_\alpha$

求导，可得：

$\frac{\partial \dot x_i}{\partial \dot q_\alpha}=\frac{\partial x_i}{\partial q_\alpha}$

①

另外，还是由复合函数求导法则：

$\frac{d}{dt} \left( \frac{\partial x_i}{\partial q_\alpha} \right)=\sum_{\beta}{\frac{\partial ^2x_i}{\partial q_\beta\partial q_\alpha}\dot q_\beta}=\sum_{\beta}{{\frac{\partial }{\partial q_\alpha}}\left( \frac{\partial x_i}{\partial q_\beta} \right)\dot q_\beta}$

因

$\dot q_\beta$

与

$q_\alpha$

无关。所以上式变成：

$\frac{d}{dt} \left( \frac{\partial x_i}{\partial q_\alpha} \right)=\frac{\partial }{\partial q_\alpha}\sum_{\beta}{{}\left( \frac{\partial x_i}{\partial q_\beta} \dot q_\beta\right)}=\frac{\partial \dot x_i}{\partial q_\alpha}$

②

实际上就是

$\frac{d}{dt} \left( \frac{\partial x_i}{\partial q_\alpha} \right)$

可以交换求导次序。

把 ① 和 ② 代入

$P_\alpha$

的表达式，得：

$\begin {align} P_\alpha &= \sum_i{ \left[\frac{d}{dt} \left( \frac{\partial T}{\partial \dot{x}_i}{\frac{\partial x_i}{\partial q_\alpha}}\right)- \frac{\partial T}{\partial \dot{x}_i}\frac{d}{dt} \left( \frac{\partial x_i}{\partial q_\alpha} \right) \right]} \\\\ &=\sum_i{ \left[\frac{d}{dt} \left( \frac{\partial T}{\partial \dot{x}_i}{\frac{\partial \dot x_i}{\partial \dot q_\alpha}}\right)- \frac{\partial T}{\partial \dot{x}_i} \frac{\partial \dot x_i}{\partial q_\alpha} \right]} \\\\ &= \frac{d}{dt} \left( \frac{\partial T} {\partial \dot q_\alpha}\right)- \frac{\partial T}{\partial q_\alpha}\\ \end {align}$

把算出的

$P_\alpha$

和

$Q_\alpha$

代回原方程有：

$\frac{d}{dt} \left( \frac{\partial T} {\partial \dot q_\alpha}\right)- \frac{\partial T}{\partial q_\alpha}=Q_\alpha$

这就是拉格朗日方程。如前所述，如果物体受力为保守力，广义力还可表示成势能的函数，于是方程可写成：

$\frac{d}{dt} \left( \frac{\partial T} {\partial \dot q_\alpha}\right)- \frac{\partial T}{\partial q_\alpha}=- \frac{\partial V}{\partial q_\alpha}$

移项合并就可得到最常见的保守系的拉格朗日方程：

$\frac{d}{dt} \left(\frac{\partial{L}}{\partial{\dot{q}_\alpha}} \right)-\frac{\partial{L}}{\partial{q_\alpha}}=0$

其中

$L=T-V$

, 是体系的动能与势能的差，称为拉格朗日量。

还要说明的是，上面的推导是基于一个质点的运动，其实很容易就可以推广到 N 个质点的力学系统。只需要把所有物体的自由度都加到求和号里，把求和总数由 3 变成 3N 就可以了，其他一切不变。

至此，终于得到“一劳永逸地解决所有力学问题”的方程。不得不说，拉格朗日实在太伟大了。

再来看看欧拉方程。

引入欧拉方程的目的很单纯，就是要解决“最速降线”问题：一个小球在只受重力、不计摩擦的情况下，从一点 A, 以何种曲线运动到不高于 A 的 B 点，使整个过程所需的时间最短？

把整个过程分成一系列无限小元过程，则下落的总时间为：

$t=\int_A^B{dt}$

只有这个式子没用，关键要把时间和轨道方程联系起来。设水平向右为

$x$

轴正方向，设竖直向下

$y$

轴为正方向，设曲线方程为

$y=y(x)$

下落过程中，小球重力势能不断转化为动能，于是

$mgy=\frac12mv^2$

于是

$v=\sqrt{2gy}$

也就是，当小球运动到

$y$

这个高度时，速度的大小。而在高度

$y$

处，一小块轨道的弧长为：

$ds=\sqrt{dx^2+dy^2}=dx\sqrt{1+y'^2}$

所以小球在轨道上运行一段弧长所需的时间，也就是一个元过程的时间为：

$dt=\frac{ds}{v}=\frac{dx\sqrt{1+y'^2}} {\sqrt{2gy}}$

于是整个过程所花的时间：

$t=\int_A^B{\sqrt{\frac{1+y'^2}{2gy}}dx}$

其中

$y$

和

$y'$

都是

$x$

的函数，这就把时间和轨道的曲线方程联系起来了。到此为止都很容易理解。但问题才刚刚开始：什么样的

$y(x)$

才能让

$t$

是最小的呢？

这里插一句，“最速降线”问题是约翰·伯努利（1667-1748）为了和同时代的其他大神飚智商在 1697 年创造出来的题目。当时除了约翰本人以外一共四个人算出了答案，他们是：约翰的哥哥雅克布·伯努利（1654-1705），约翰的老师莱布尼茨（1646-1716），约翰的学生洛必达（1661-1704），还有牛顿（1643-1727）。他们的解法各有特点，其中不乏特别巧妙的地方，比如约翰就利用了几何光学的费马原理给出了非常简洁的推导。不过这里不打算详细介绍这些解法，因为这和本文主题并无多大关系。

这里想说的是约翰·伯努利的另一个学生欧拉（1707-1783）基于最速降线问题提出的一种思考问题的套路——变分法。

还接着上面的式子说。刚刚算出小球滚落的时间为：

$t=\int_A^B{\sqrt{\frac{1+y'^2}{2gy}}dx}$

这本质上是一个求极值的问题，也就是：当

$y$

为何种形式的函数时，

$t$

取极值？欧拉不仅仅局限于这一个具体的函数形式，他把问题抽象为更一般的形式：

$J(y)=\int_A^B{F(x,y,y')dx}$

即上式中当

$y$

为何种形式的函数时，

$J$

取极值？

注意这里

$J$

的取值取决于函数

$y$

，即对于每一种

$y$

的形式，都有一个

$J$

的数值与之对应。于是

$J$

就是关于函数

$y$

的“函数”。但这种“函数”并非通常意义的函数，因为它的自变量不是数，而是函数。这种“自变量是函数的函数”，就是泛函。欧拉就这样把一个具体的求“最速降线”问题升华成了一个抽象的求“泛函极值”的问题。

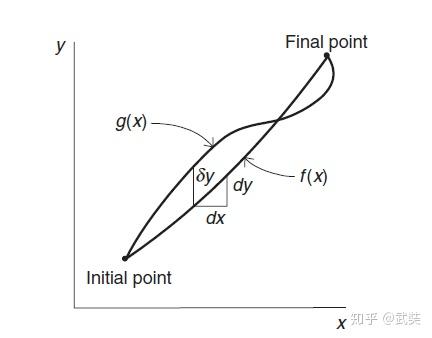
如图，AB 是两个固定点，函数

$y$

可理解为 AB 之间的一根琴弦。现在轻轻拨动琴弦，让函数

$y$

有一个小变化，变为

$y+\delta y$

, 这里

$\delta y$

就称为函数

$y(x)$

的变分，也就是一个函数整体的变化。为了和数的变化——微分区别，用希腊字母

$\delta$

表示。

$y$

变化时，泛函

$J$

也相应改变。改变量为：

$\begin{align}J(y+\delta y)-J(y) &=\int_A^B{[F(x,y+\delta y,y'+\delta y')-F(x,y,y')]dx}\\ &=\int_A^B{[\frac{\partial F}{\partial y}\delta y+\frac{\partial F}{\partial y'}\delta y']dx} \end{align}$

这个泛函的变化量就称为泛函的变分，记作：

$\delta J=\int_A^B{[\frac{\partial F}{\partial y}\delta y+\frac{\partial F}{\partial y'}\delta y']dx}$

现在要求的是泛函

$J$

何时取极值。大家都知道如果求一个函数

$f(x)$

的极值，只需令

$f'(x)=0$

就可以求出。可是泛函的自变量是函数，它极值点怎么求？

设问题的解，即让泛函取极值的函数为

$y=y(x)$

. 让

$y$

有一个小变化，变为

$y(x)+\delta y$

. 把变分表示为一个小参数和任意一个函数的乘积：

$\delta y=\varepsilon\cdot \eta (x)$

这样，泛函

$J(\varepsilon)$

就成了参数

$\varepsilon$

的函数。这样，就把关于函数

$y$

的泛函，转化成了关于参数

$\varepsilon$

的函数，这就巧妙地把泛函极值问题转化为函数极值问题。因为泛函取极值时，参数

$\varepsilon=0$

，所以有：

$J'(0)=\frac{dJ}{d \varepsilon}|_{\varepsilon=0}=0$

泛函变分可表示为

$\begin{align} \delta J &=J(\varepsilon)-J(0) \\ &=J'(0)\cdot\varepsilon \end{align}$

所以

$J'(0)=0$

和

$\delta J=0$

是等价的。于是整个问题就转化为：

$y$

取何形式时，泛函

$J$

的变分等于零？也就是：

$\delta J=\int_A^B{[\frac{\partial F}{\partial y}\delta y+\frac{\partial F}{\partial y'}\delta y']dx}=0$

用分部积分法把上式第二项做代换：

$\begin{align} \int_A^B{\frac{\partial F}{\partial y'}\delta y'dx} &=\int_A^B{\frac{\partial F}{\partial y'}\frac{d(\delta y)}{dx}dx}\\ &=\int_A^B{\frac{\partial F}{\partial y'}{d(\delta y)}}\\ &=\left[ \frac{\partial F}{\partial y'}{\delta y} \right]_A^B-\int_A^B{\frac{d}{dx} \left({\frac{\partial F}{\partial y'}} \right) {\delta y} dx}\\ \end {align}$

代回，得：

$\delta J=\left[ \frac{\partial F}{\partial y'}{\delta y} \right]_A^B+\int_A^B{\left[ \frac{\partial F}{\partial y}\delta y-\frac{d}{dx} \left({\frac{\partial F}{\partial y'}} \right) {\delta y} \right] dx}$

因为端点 AB 固定，所以在 A 点和 B 点处

$\delta y=0$

, 所以上式第一项为零，所以：

$\delta J=\int_A^B{\left[ \frac{\partial F}{\partial y}-\frac{d}{dx} \left({\frac{\partial F}{\partial y'}} \right) \right]{\delta y} dx}$

要让上式为零对于任意

$\delta y$

都成立，必须有：

$\frac{\partial F}{\partial y}-\frac{d}{dx} \left({\frac{\partial F}{\partial y'}} \right) =0$

也就是：

$\frac{d}{dx} \left(\frac{\partial{F}}{\partial{y'}} \right)-\frac{\partial{F}}{\partial{y}}=0$

这就是欧拉方程：要让泛函

$J(y)=\int_A^B{F(x,y,y')dx}$

取极值，函数

$y(x)$

必须满足的方程。

只要把具体的关系

$F=\sqrt{\frac{1+y'^2}{2gy}}$

代入欧拉方程，即可求得最速降线。最终的解可以用参数方程表示：

$\begin {cases} x=\frac12k^2(\theta -\sin \theta)\\\\ y=\frac12k^2(1 -\cos \theta)\\ \end {cases}$

这是一条摆线，也叫旋轮线。这里就不多说了。

1728 年，欧拉用变分法求解最速降线问题，得到欧拉方程。60 年后，小欧拉 30 岁的拉格朗日完成《分析力学》，提出拉格朗日方程。这是在时间、空间、思想上都完全独立的两条线，却神奇地得到了一个长得一模一样的方程。后来大家合称它们为欧拉 - 拉格朗日方程。

又过了 50 多年，小拉格朗日 70 岁的爱尔兰人哈密顿让这两条独立的线交汇。他看到两个方程的一致性，自然地想到：既然欧拉方程背后对应着一个取极值的积分，拉格朗日方程自然也有。这个积分就是拉格朗日量对时间的积分，也就是哈密顿作用量。一个力学体系，实际走过的路径必取哈密顿作用量取极值的那一条，这就是哈密顿原理。

像这样把一个老方法应用到新问题，得到新结论的故事，在物理学历史上比比皆是。

比如后来，又是哈密顿，把勒让德变换应用到拉格朗日方程，使之降阶，导出了他的哈密顿方程，创立和拉格朗日力学同样重要的哈密顿力学。理论力学双峰并立之格局始成。

这是后话。

完。

哈密顿原理和拉格朗日函数的由来是怎样的？

相关推荐