我觉得题主可能忽视了月球拥有大气层背后代表的意义,那就是月球必须先极大地增重,然后才配拥有大气层。
现在的月球的质量太小,不足以拥有维护稳定大气层的引力场。我们来算一下。
一个星球想要拥有大气层的前提之一,是要保持气体分子在星球上的运动速度远小于星球的逃逸速度。我们下面计算月球上不同气体的运动速度和月球的逃逸速度。
当物体的动能等于其重力势能时,其对应的速度就可以使物体逃逸,这个速度满足:
1/2mv^2 = GMm/r
其中,m 这里代表气体分子的质量, M 是月球的质量,大概是 7.34767x10^22 kg,G 是引力常数,r 是质心之间的距离,按月球半径算为 1737400 m。
所以,可以得到月球的逃逸速度是
相对比咱们得地球,这个速度就小太多了,地球的逃逸速度是 11.2 km/s
所以,任何碰巧以大于 2375.2 m/s 的速度向上飞行的气体分子都将逃离月球并且不会返回。
这就引出了另外一个计算,气体分子的传播速度有多快。
这就要提到,麦克斯韦 - 玻尔兹曼分布,即 Maxwell-Boltzmann Distribution,如下图。它描述了气体分子在不同速度下的概率分布。根据这个分布,在热平衡状态下,某一速度对应的分子数目可以表示为:
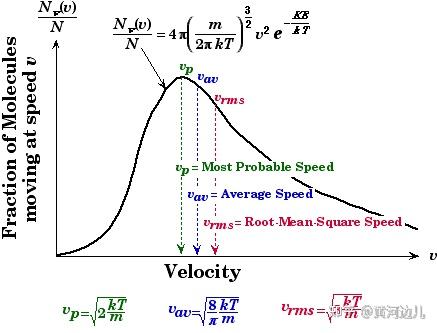
根据这个分布,我们可以得到,气体分子的平均速度,均方根速度等不同速度。常用的气体速度是其均方根速度,表示为:
我们可以根据此式,计算不同气体分子在月球上的运动速度。月球上的温度范围在 -173°C 到 127°C,我们算一下 100°C ,即 400.15K,氧气分子和氢气分子的运动速度。
氧气分子的摩尔质量是 32g/mol,对应的氧气分子的质量
,
玻尔兹曼常数
代入上面的均方根公式可以得到,氧气的运动速度是
类似的,氢气的均方根运动速度是:
相比较于月球的逃逸速度 2375.2,两者都接近,尤其是氢气。值得一提的是,计算这个速度是氧气和氢气运动速度的均方根速度,实际中,分子有时会快于,有时会慢于这个速度,一旦这个速度超过了逃逸速度,那么就会离开月球,在漫长的月球演化历史中,结果就是几乎所有的气体都逃离了月球。理论上,月球也是有大气层的,但是非常非常稀薄。
好了, 说了这么多,想说明一点,按照题目中的假定,月球拥有了大气层,其实,背后隐含的意义是月球的质量变大了,这样才足以支撑大气层的存在,气体分子不足以快速的逃离。
那么问题就是,月球变大,拥有了大气层后,会有什么影响呢?
首先,就是地球上会形成超级大海啸,沿海地区已经不再适合人类居住。
而且,会导致潮汐摩擦效应增强,这会加速地球的自转减慢,也就是一天的长度逐渐变长。
另外,月球的轨道也会由于其质量变化而逐渐更加接近地球,或者更加椭圆。这可能是对人类致命的。
先写到这吧,点个赞吧~
因为回答了几个 @知乎科学 举办的 脑洞发问局 的问题,不少评论( @云海看星辰@二阶连续可导@坏了的 venture@讣告@温水煮呆蛙 )在讨论,这些脑洞问题没有意义。这里一并做一下解释:
很多物理公式都是基于大量实验观测数据或者理论推导,当这样一个单一的公式冷冰冰的摆着大家面前的时候,是抽象的,是很难产生兴趣的,甚至是枯燥的。我回答和提出这些脑洞问题的初衷之一,是希望通过一个个有趣的脑洞问题,把这些本身抽象化的公式,实例化,趣味化,帮助大家接受。
比如,上面这样一个完全不可能的脑洞问题,就向大家传递了一个抽象的物理公式:麦克斯韦 - 玻尔兹曼分布。如果真的有本物理书摆在你面前写了麦克斯韦 - 玻尔兹曼分布,你可能看都不看一眼,但是因为有了这样一个有趣的题目,至少你看了这个公式,甚至了解了这个公式是干什么的。
其他脑洞问题,如果大家感兴趣,可以看这些:
这个回答通过一个脑洞问题,解读了屈服强度,体积弹性模量,体积热膨胀系数,终端速度等
如果把一个实心钢球扔进马里亚纳海沟,会发生什么?
这个回答通过一个脑洞问题,解读了Schwarzschild 半径
如果把木星压缩成一个篮球,它会变成一个黑洞吗?
这个回答通过一个脑洞问题,解读了贝努力原理
当风筝的线足够长时,风筝能飞到最高距离是什么?为什么?
这个回答通过一个脑洞问题,解读了普朗克辐射定律
是否存在一个热力学温度下限,使得处于该温度的黑体不再发出黑体辐射?
这个回答通过一个脑洞问题,解读了质光关系
如果向太阳的核心注入相当于木星体积 1000 倍的水,太阳会熄灭么?

 微信扫一扫
微信扫一扫 



