省流版:
不存在这样的操作。
因为重复的操作会构成一个有限的循环群,它是一个阿贝尔群。但考虑到魔方群是一个非阿贝尔群,它不可能同构于一个阿贝尔群。因此不存在。
一、魔方群概念的引入
这其实是一个相当 trivial 的问题,用数学中群论的语言就可以轻松回答这个问题,且不需要太多数学知识也能看懂这个回答[1]。
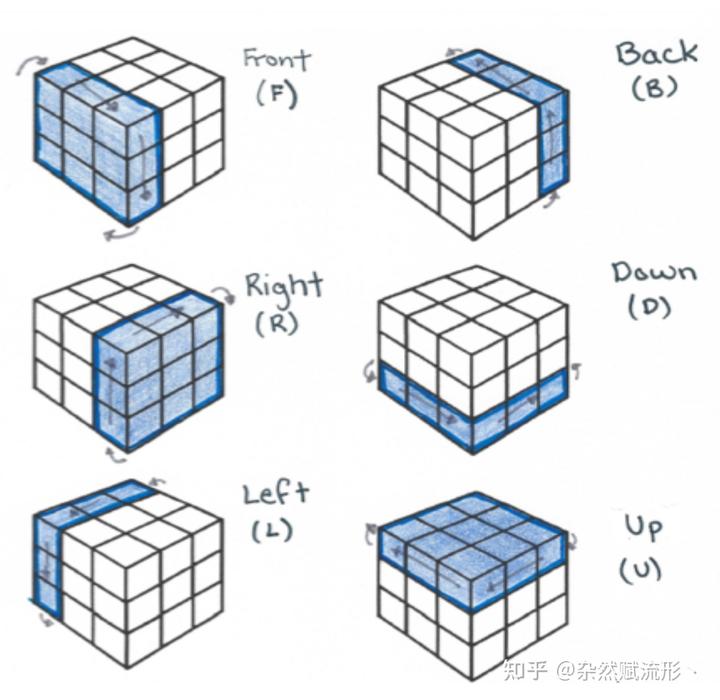
我们以常见的 3 阶魔方为例,下面这张图给出了 3 阶魔方的 6 个基本操作:
- 前面旋转 90°(F, front),
- 后面旋转 90°(B, back),
- 左面旋转 90°(L, left),
- 右面旋转 90°(R, right),
- 上面旋转 90°(U, up),
- 下面旋转 90°(D, down):
这里的 90° 都是指正面对着要操作的那个面,顺时针旋转 90°。
魔方的每个面共有 9 个色块,总共 6 个面。那么一个 3 阶魔方包含 6×9=54 个色块,除去每个面最中间保持不动的色块(因为无论怎样旋转魔方,它们始终不变),魔方总共包含 54-6=48 个可移动色块。我们可以给这 48 个色块进行进行编号,如下图所示:
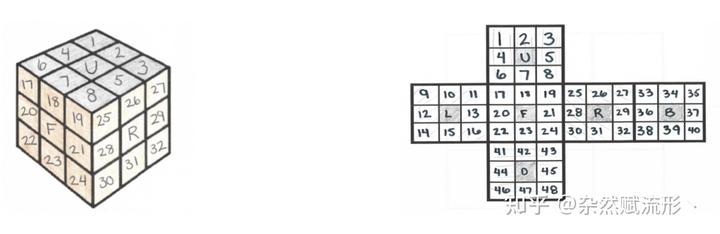
只要确定这 48 个数字的位置,我们就确定了一个魔方目前的状态。在这种表示下, 对魔方的一个操作可以表示成一部分数字的置换。
当我们拿到一个初始复原状态(简记为
)的魔方,进行随机打乱,可以得到一个混乱状态(简记为
)的魔方,即
上面右边这一组操作符号是我随便写的。我们把这一组操作的复合简记为
,即
。那么,我们只要遍历对魔方所有可能的操作
,就可以从复原的状态开始,得到任何一种可能的打乱状态。在数学中,这些所有可能操作
的集合叫做群。对于魔方而言,我们把它叫做魔方群(Rubik's Cube group)。
取
的逆操作
,它表示的是如何从打乱的状态
开始,复原到初始状态
。那么我们可以得到
。所以魔方复原问题,转化成数学语言来说就是,如何从给定状态 ,找到魔方群中的某个群元素
,使得
。
听上去这好像很简单,但实际玩过魔方的人都知道,魔方复原非常困难。
这是因为魔方群
的是一个非常庞大的群,前面我们提到可以用 48 个数字的置换来表示魔方的一个操作,排除掉某些不可能的置换(比如你不能把魔方的一个色块给拆下来再转个角度拧回去),所以魔方群是一个 48 阶置换群
(它表示所有 48 个数字可能的置换)的子群,而
总共有
个元素,可能大家不能直观体会这个数字的庞大,实际上
所以
是一个 62 位数。但魔方群
是
的子群,似乎要简单一点,但也简单不到哪里去。具体分析魔方群的元素个数是一个不轻的体力活,我们这里不去具体证明,直接上答案[2]:
它是一个 20 位数,在这庞大的集合里找到使得魔方能够复原的 1 个元素,听上去就不是那么容易的事(不过它们都有固定公式可以套用,所以实际上也没这么夸张)。
二、魔方群是一个非阿贝尔群
在做了上面这些铺垫之后,让我们回到题主的问题:
是否存在一套动作,使得对于任意状态的魔方,只需要重复该动作到一定次数,都一定能还原?
这其实就是一个超级简单的数学问题。假设我们存在这样的一个操作,记为
,那么对于任何一个可能的魔方状态
,通过反复对它进行
这种操作,可以回到初始状态
。转化成数学语言,即存在某一个非负整数
,使得
这里的操作
显然是可逆的,因为我们对魔方转一个角度后,可以再反过来转同样的角度,就恢复到了转之前的状态。因此,我们可以得到
这样,我们可以从魔方复原的初始状态
开始,通过不断的进行
操作的逆
,可以得到任何一种可能的魔方状态。因此,
的集合就构成了一个群,显然它也是魔方群。即,
上式左边的
代表由 F, B, L, R, U, D 六个基本操作生成的群。而右边的
代表由
操作生成的群,注意它是一个循环群,因为它只有一个生成元
。由于这两个群都是魔方群,它们是同构的,用
表示。
所以到目前为止,题主的问题我们可以将其转化为:魔方群是否同构于循环群?
这个问题非常简单。注意
是一个阿贝尔群(即群中任意两个元素的乘积满足交换律),这是因为
。
但另一方面
却是一个非阿贝尔群。这可以举一个例子就容易判断得出,见以下图片:
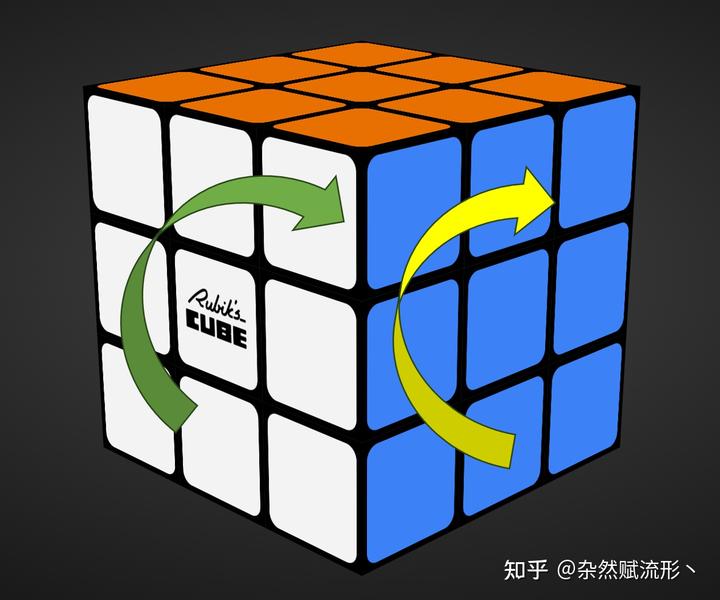
我们分两种情况对魔方进行操作,
- 先对前面顺时针旋转 90°,再对右面顺时针旋转 90°,即
;
- 先对右面顺时针旋转 90°,再对前面顺时针旋转 90°,即
;


简单对比就可以发现,
,所以作用顺序不一样得到的魔方状态是不同的。因此魔方群实际上是一个非阿贝尔群。
由于阿贝尔群和非阿贝尔群不可能同构,因此不存在这样的操作,使得任意状态的魔方,反复进行此操作便能复原。
另一个角度,我们也可以从数学上来进一步验证。设有某两个整数
使得
,
,则我们可以得到:
这和我们前面通过实践得到的
相矛盾,因此假设不成立,不存在这样的操作
。
三、补充内容
实际上魔方群的结构远比循环群复杂的多,它和以下群同构,
这里的
是半直积(semidirect product)的意思。
另外还有一点可以补充的是,尽管我们在一开始通过六个基本操作(F, B, L, R, U, D)生成了魔方群,但魔方群生成元的最小个数并非是 6,它的最小个数是 2 (即魔方群的秩是 2[3])。所以对于题主的问题,还可以进一步回答:
不存在一套动作,使得任意状态的魔方,只要不断重复该动作就可以复原。但可以只用两套动作,不断重复进行这两套动作,就可以使得魔方复原。
当然了,你要注意到,对于一阶魔方而言,只用一套动作显然是可以的。
我个人比较擅长复原 1 阶魔方


 微信扫一扫
微信扫一扫 



