奥利给不等式就是:

哈哈哈哈,开个玩笑~
其实,这是个谐音,“奥利给不等式”指的是“ALG 不等式”(Arithmetic-Logarithmic-Geometric mean inequalities),中文又称“对数均值不等式”[1]。
定义是:
即对于任意两个非负且互不相等的数
和
,两者的算术平均数(Arithmetic mean)
大于对数平均数(Logarithmic mean)
大于几何平均数(Geometric mean)
。
对应的证明方法有很多,我找到了一个由 Roger B. Nelsen 教授给出的图解证明法[2],这也是我所见过的最为直观简洁的奥利给不等式证明方法,但是由于其原文中的公式有些错误,所以这里重新写一遍。
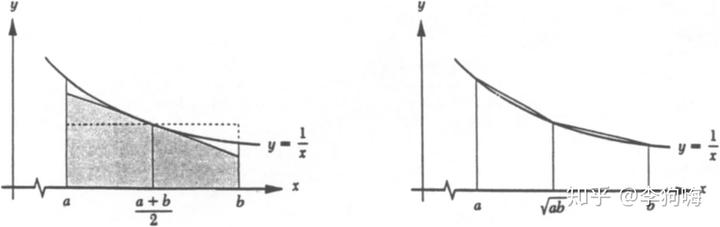
思路其实就是对比函数
在区间
所围的面积与一个通过“内切”(左边图)形成的梯形面积与两个通过“外接”(右边图)形成的梯形面积,进而得到不等式关系。
很显然,两种情况下,函数
在区间
所围的面积都为:
对于左边的图,根据积分所得面积与梯形面积的关系有:
(注意这里的梯形可以看做是长为
,高为
的矩形)
对于右边的图,根据积分所得面积与两个梯形面积和的关系有:
(开始吟唱:梯形的面积是上底加下底的和乘高除二!)
综上有:
而对于题主的问题,关于
与
的关系就很好比较了。
由奥利给不等式有:
现在只需要令
则有:
所以当
时,有:
当
时,有:
当
时,有:
《直观の数学》专栏

 微信扫一扫
微信扫一扫 



