这是一个经典的数学建模问题,正好做过一个相关题目。
《植物大战僵尸》是一塔防类策略游戏,玩家在每一关卡中种植植物抵御各种僵尸入侵。
本文在分析植物大战僵尸人机博弈机制的基础上对博弈逻辑进行了模拟,通过遗传算法、动态规划求解植物大战僵尸一般通关模型,得到通关最优策略及最大阳光数量,并使用随机模拟及隐马尔科夫神经网络对 未知僵尸生成情况下的关卡进行模拟分析求解,
使用统计分析方法得到更复杂情况的最优策略及最大阳光数量期望。
游戏规则
基本游戏规则:
1.以游戏开始时刻为第 0 秒(秒为基本时间单位),玩家在场地任意处种植植物(需要阳光),植物可立即工作。
2.游戏场地由横平竖直,大小相等的网格组成,一个格子内仅能种植一株植物,但能容纳多个僵尸。
3.僵尸仅在屏幕最右侧产生,从右向左以直线前进,僵尸依次吃掉沿途的植物直至被植物袭击杀死并立即消失。若果僵尸到达屏幕的最左侧,则通关失败,游戏结束。
4. 植物分为生产植物和攻击植物。 生产植物在种植后可以持续产生阳光。 单击阳光即完成收集与存储,阳光达到一定量后可种植植物。
5.僵尸在吃植物时需停止,在吃完植物后才能继续前进。受伤但未被完全吃掉的植物,其产量或攻击作用按受伤比例减少 。游戏者尽量不要让僵尸吃到植物。
6. 游戏还提供铲子,可用来铲除已种下的植物。移除后,可在该处种植新植物。
7.玩家必须在最后一个僵尸出现的 20 秒内将其击杀,否则游戏失败。
问题提出
问题一:若场地大小为
格的条形区域,每隔 9 秒刷新一个僵尸(从第 0 秒开始有僵尸出现),游戏时已知僵尸出现顺序与种类。试给出一般情况下玩家通关附件 4 中一、二关的最优策略。
问题二:若场地大小为
格的长方形区域,每隔 6 秒刷新一个僵尸,游戏时已知僵尸出现顺序与种类。试给出一般情况下玩家通关附件 4 中第 3 关的最优策略。
问题三:若场地大小为
格的长方形区域,每隔 6 秒刷新一个僵尸,在游戏时未知部分僵尸出现的顺序、位置与种类。试给出僵尸不同生成情况下玩家通关第 4 关的通关策略(或不能通关) 及最终阳光数量。
植物大战僵尸数学模型相关参数定义
(1) 植物
对于游戏中用于购买种植植物的“货币”阳光,本文将总阳光数记作
,在一局游戏中产生的阳光记作
,消耗的阳光总数记作
。本文以
表示四种能够生产阳光的植物;以
表示四种具有攻击能力的植物。对于能够生产阳光的植物,本文将四种植物产生阳光速度记作
,生命力记为;
;同理,对于具有攻击能力的四种植物
本文将其攻击力记作
,攻击速度记作
,其生命力记为
。
(2)僵尸
对于游戏中出现的普通僵尸、铁桶僵尸、巨人僵尸、暴走僵尸四种有着不同生命值、攻击力、移动速度的僵尸,本文将其记作;
,对于这四种不同类型的僵尸的生命(HP)分别记作
,他们的攻击力分别记为
,僵尸前进速度记作
。
(3)阳光
对于一局游戏中总阳光数记作
,在一局游戏中获得的阳光记作
,消耗的阳光总数记作
及初始阳光数
,有如下关系:
对于生产的阳光速度
,有:
其中
表示不同种类的能够产生阳光的植物产生 1 阳光所用时间,因此,一局游戏中产生阳光的总数量
可记作:
式中
表示对于此株植物被铲除时时间或游戏结束时时间,
表示此株植物被种植下时的秒数。
由于受伤会对植物产量或攻击作用产生影响,其产量会按受伤比例减少 ,故有:
其中
表示受到攻击后该植物产生阳光的速度,
表示该植物当前生命值。
而一局游戏中消耗的总阳光数目
可以表示为种植所有攻击性植物与所有生产阳光的植物所需阳光和:
式中
表示种植第
株生产阳光类植物需要消耗的阳光数,且此株植物是第
类,
表示种植第
株具有攻击性植物需要消耗的阳光数,且此株植物是第
类。
(4)生命值
僵尸在收到植物攻击时,其生命值(HP)在不断降低,同理,植物被僵尸吃掉过程中,其生命值(HP)在不断降低。对于在游戏第 t 秒场上从左至右第 u 个僵尸时的生命值可表示为
,第 w 个具有攻击性植物在游戏第 t 秒时的生命值可表示为
,第 s 个可生产阳光的植物在游戏第 t 秒时的生命值可表示为
。
(5)平面直角坐标系
本文为刻画植物与僵尸具体位置,以游戏场地左下角为原点,水平方向为 x 轴,竖直方向为 y 轴建立如图所示的平面直角坐标系,本文假设植物均只能种在方格中间,僵尸在方格中间至方格右侧时能够攻击植物,且僵尸总是沿着植物所在的直线(即图中虚线)前进的,设在第 t
秒时,游戏场地上有 m 个具有攻击力的植物,n 个可产阳光的植物,r 个僵尸。

(6)植物、僵尸坐标
对于场地上植物与僵尸实时坐标,本文分别以
、
、
表示 t 秒时僵尸、具有攻击力的植物、能生产阳光的植物坐标,由于本文假设 植物均只能种在方格中间,且僵尸总是沿着植物所在的直线(即图中虚线)前进的,故式中:
(7)僵尸生命与数量
当第 t 至 t+1 秒时,当前场地上植物对僵尸造成的总伤害
可表示为:
则在
秒时对应行最左端僵尸生命值(HP)可表示为:
为僵尸的总血量,
表示该行最左边僵尸的 HP。
对于僵尸数量,每当前时间 t 为 9 的整数倍时,自动生成一个僵尸直至所有 30 个僵尸全部生成,每当植物打死一个僵尸时,僵尸总数就减少一个直至打死所有僵尸。
对于发射的子弹在坐标系中坐标,本文记作
,式中
表示当前第 t 秒时子弹所在位置,
表示发射该子弹的植物所在的位置,
表示子弹发射时刻。若在 t 时刻场上位于
的植物发射了一枚子弹
射击僵尸
,则在 t 秒时有:
t+1 秒时,有:
式中
与
表示 t+1 秒时子弹若没有碰到僵尸理论上的位置。若 t+1 秒时子弹若没有碰到僵尸理论上的位置坐标大于改行最左端僵尸,即:
时,僵尸会收到攻击,故有:
式中
表示 t+1 秒时僵尸血量,
表示该植物攻击力
在植物攻击时若:
则这部分伤害会在 t+2 秒时造成。
(8)植物生命
当 t 秒时僵尸进入可攻击植物范围内,即:
或
僵尸在上述范围时,僵尸就会立即停止前进开始吃植物,植物在 t+1 秒时生命值即为:
或
通关模型的建立
约束条件
为给出一般情况下玩家通关的最优策略,对于一关关卡顺利通过的要求是:打败所有僵尸,
同时,题目要求最后一个僵尸死亡时间出现后 20s 后必须完成击杀随即结束游戏并保证阳光数最大,故游戏胜利结束时长一定等于最后一个僵尸死亡时间,且游戏结束时间一定在在最后一个僵尸出现后,并在最后一个僵尸出现后 20s 内,即当
且
时有:
式中
表示击杀最后一个僵尸的时刻,
、
分别表示一关关卡中僵尸总数与僵尸出现间隔时间,且
式中,
表示游戏结束时长,对于关卡一、二中
与
:
关卡三中:
在种植植物过程中,已种植植物且未被铲除的格子不允许叠加种植,即:
且植物种植的时间必须在游戏结束前,即最后一个僵尸出现后 20s 前,即:
式中
表示植物可种植的时间。
此外,为了使得游戏结束时,阳光的存量能达到最大,故在最后一个僵尸出现时可通过减缓僵尸前进的方式(即不断在僵尸刚吃完该格植物瞬间立刻补种非攻击性植物)来使得游戏时间尽量延迟,为了在确保阳光尽可能多的前提下尽量延迟游戏结束时间。
当出现最后一个僵尸时,
本文先在能尽可能多的生产阳光的前提下将僵尸血量降低至仅攻击一次便能杀死僵尸,
此后,对场上可生产阳光植物与现有阳光进行分析:
(1)
若在僵尸吃掉一个可产阳光的植物的攻击时间加上离开在该格中能够攻击到植物范围(由公式可知,僵尸可攻击植物范围为植物种植格的右半部分)的移动时间内(僵尸离开在该格中能够攻击到植物范围的移动时间同样也是本题中在僵尸吃掉植物后还能够顺利将僵尸在此格中阻拦下的时间),所有植物生产的阳光大于种植一个可生产阳光的植物所需花费的阳光时,即:
时,(式中
表示在僵尸吃完的植物所在格补种的植物所需的阳光数,
表示在 t 秒时该僵尸血量,
表示所有能攻击该僵尸的植物的总攻击力,
表示该僵尸移动速度,
表示可生产阳光的植物的生产速度)
可通过僵尸吃掉植物瞬间立即重新补种植物的方法以达到延长游戏时间至最长时长的目的;
(2)
若在僵尸吃掉一个可产阳光的植物时间与离开该格可攻击范围时间内,所有植物生产的阳光小于种植一个生产植物的阳光时,
本文进一步对该情况分析:
对于任意一种能生产阳光的植物,僵尸前进一格时间加上僵尸吃掉该格处植物的时间一定都小于产生种植该植物成本的阳光数,即
因此,一旦场地上其余地方种植的可产阳光的植物产量不足以满足阳光数正增长时,本题此时就不对僵尸前进进行阻拦,每当僵尸吃掉一株植物时,都需进行一次判断:若将当前拥有的阳光全部用于购买一种较为合算的可生产阳光的植物,在完成购买并种植后,是否满足式(\ref{q2}),若满足就进行种植并回到情况(1),若不满足上式,就允许僵尸前进吃下一个植物,如此往复直至游戏时长达到关卡要求的总时长。
目标函数与决策变量的确定
由于本文最终的目的是在通关游戏(消灭所有僵尸)的前提下,并尽可能保留最多的阳光,故本文建立起植物大战僵尸通关策略模型,在能够于规定时间通关的前提下,使得对局中收获的阳光总数量尽可能多,根据上文分析可得,对局中收获的总阳光数取决于种植的可生产阳光植物类型,与每种植物对应种植时间及其数目与生命值,综上所述,为了使得阳光最大化一局游戏中中收获的总阳光数 S 可表示为:
最终模型的建立
综上所述,可建立起植物大战僵尸通关策略模型:
关卡 1、2:
关卡 3:
模型的求解
通过对上述模型的分析,可以判断该模型是离散优化问题,在整场游戏中对时间进行离散化处理,对每一秒通过上一秒进行模拟即可得到每一秒植物、僵尸、子弹的状态,进而递推整场游戏的情况。因此首先应该构造该游戏的模拟程序,其次再寻求解决改离散优化问题的算法。
设计模拟仿真程序
根据对植物大战僵尸游戏的数学模型化,本文基于原游戏与假设的模型对整个关卡的过程进行计算机模拟,通过输入种植植物的时间、种类、坐标信息,即可得到可视化过程以及最小初始阳光数量和整个过程的阳光增量。
在离散的每个整数秒的时间点应该对该一秒内的所有动作进行结算,所有“操作”的执行顺序会影响游戏进程以及结果,因此要良好的还原游戏的真实进程,应该对操作和操作的前置操作进行分析,下表是本文对算法中不同操作的编号:
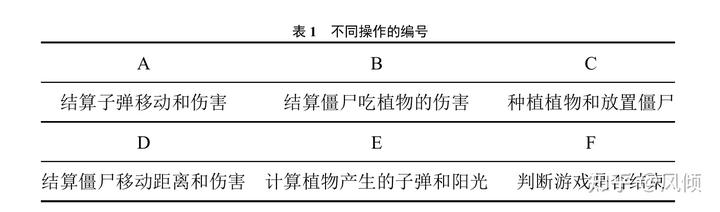
操作 — 对应的前置操作对有:D—C,E—C,C—B,B—A。
对于复杂的工作计划表可以由计划评审法或关键路径法进行求解,由于此处“操作”数量少,可以直接得到一个这些操作的拓扑序,其满足,当线性的进行拓扑排序后的操作时,能保证进行的每个操作已经进行了前置操作。操作的拓扑序即每一秒的线性流程如下:结算子弹移动和伤害、结算僵尸吃植物的伤害、种植植物和放置僵尸结算、僵尸移动距离和伤害、计算植物产生的子弹和阳光、判断游戏是否结束。
算法的设计
由于问题一和问题二都需要求解数目不定的多次操作的操作时间、种植植物编号、种植位置坐标,需要求解的决策变量数目较多且数目不定,同时模型中带有逻辑运算和非线性不等式约束,因此必须寻找能够求解维度不定的大规模离散优化问题算法。
启发式算法是一类求解大规模优化问题、可编辑性较强的算法,使用启发式算法能很好的处理一系列复杂的或带有逻辑符号的约束条件,也可以适用于决策变量数目不确定的问题,本文采用遗传算法求解。由于该问题每秒状态繁多,求解域巨大,同时可行解域又较小,本文在一般遗传算法只计算适应度的基础上增加了对惩罚值的计算,当惩罚值为 0 时,即为寻找到可行解的时候。在本文中,适应度为在模拟后得到的整个过程的阳光增量,惩罚值为
。
遗传算法具体步骤如下:

在一般情况中,“铲除”操作一定伴随着种植新的植物,本文为使决策变量更少、减小算法的复杂度,将“铲除和种植”操作定义为“替换”,即替换操作可以是单单的在无植物的方格种植植物,也可以是在一个有植物的方格消耗阳光对此植物替换,从而降低难度。
求解分析
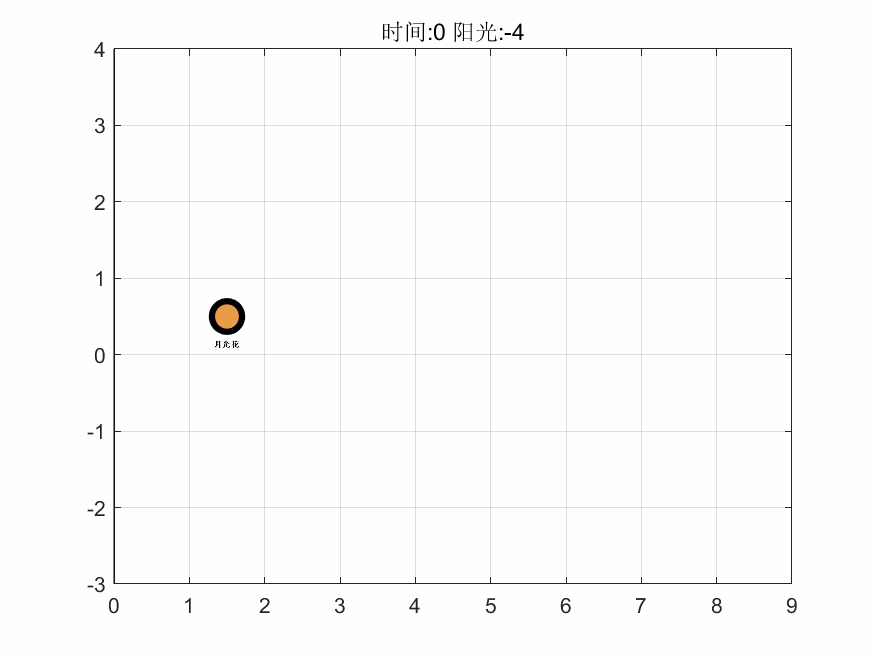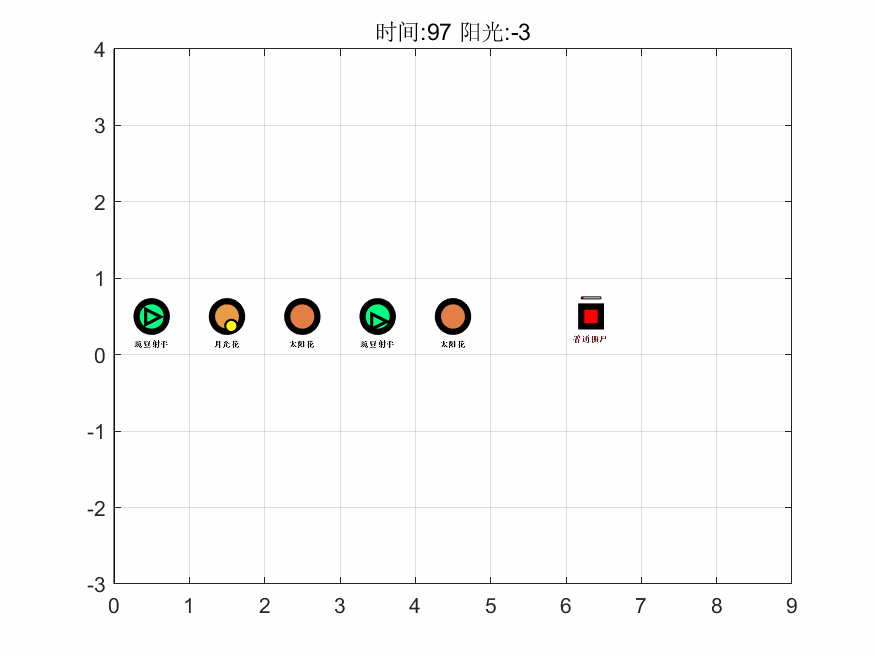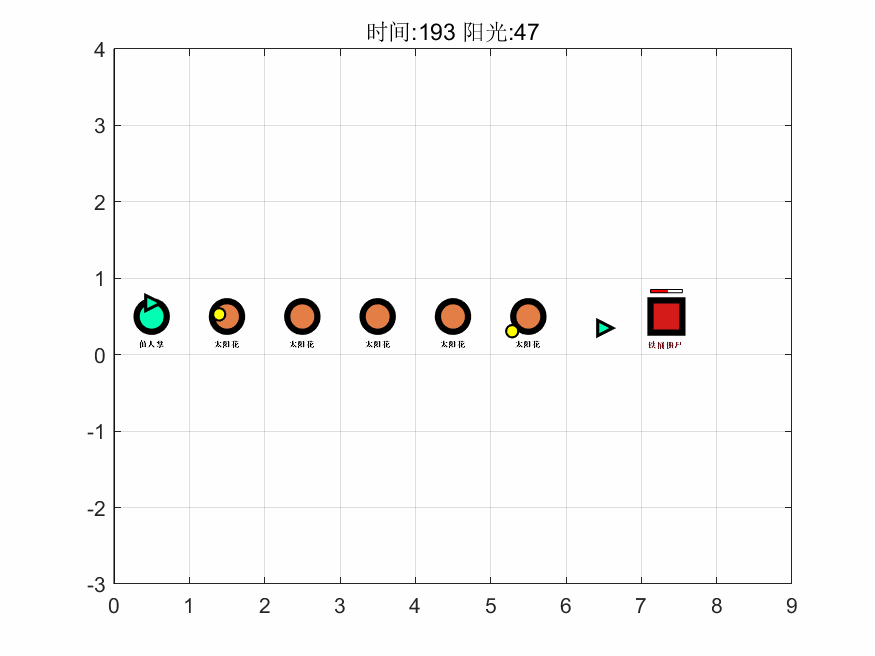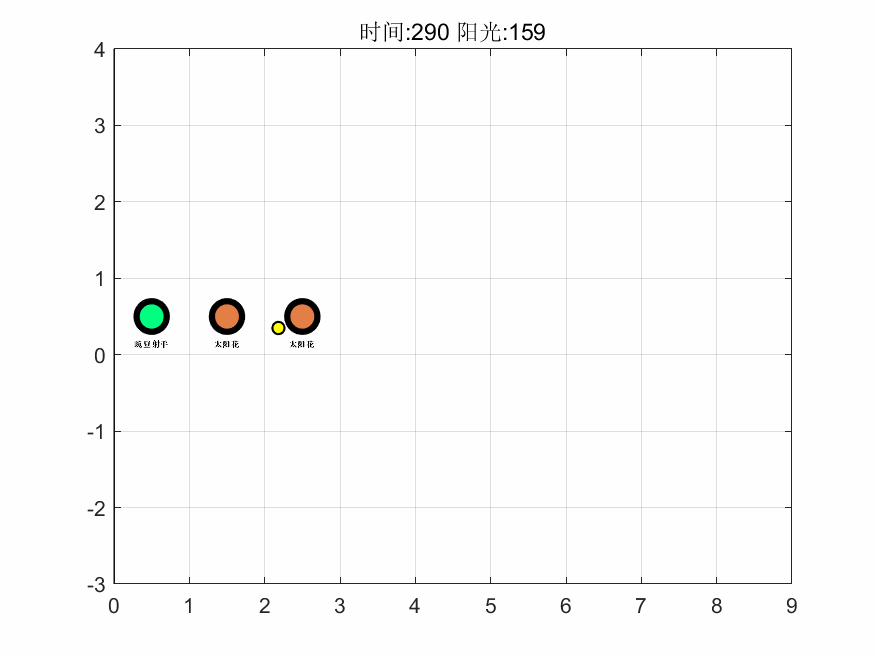
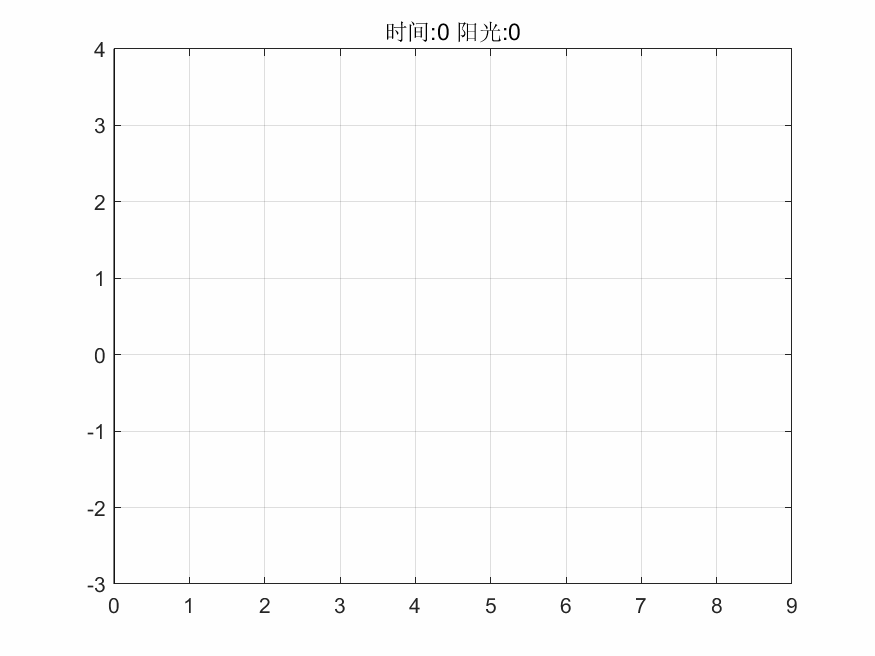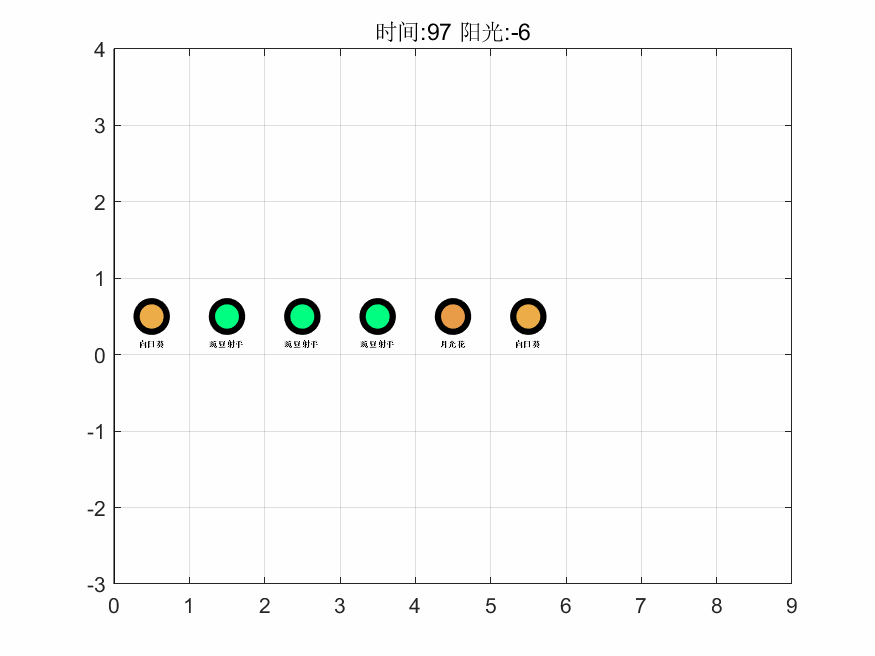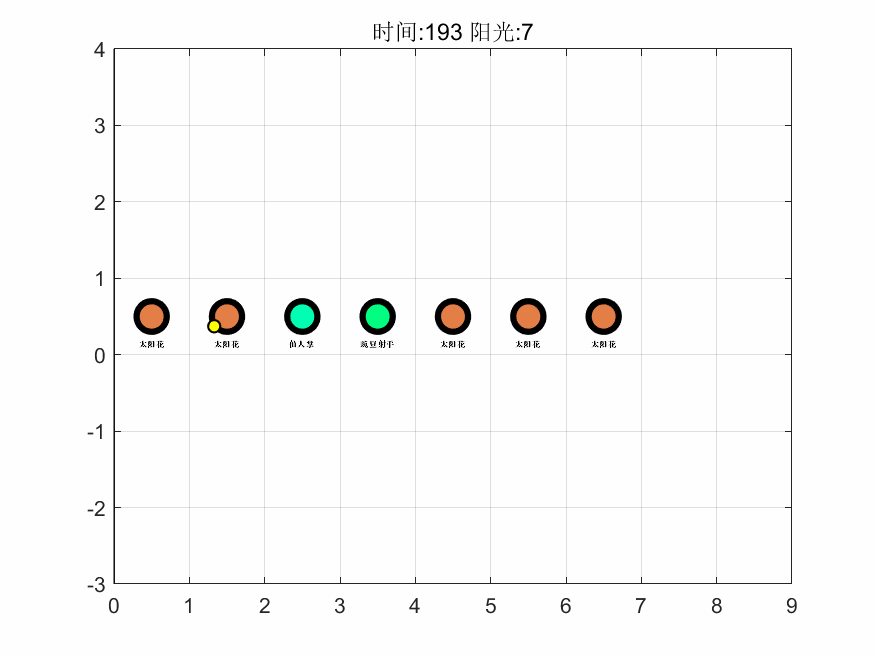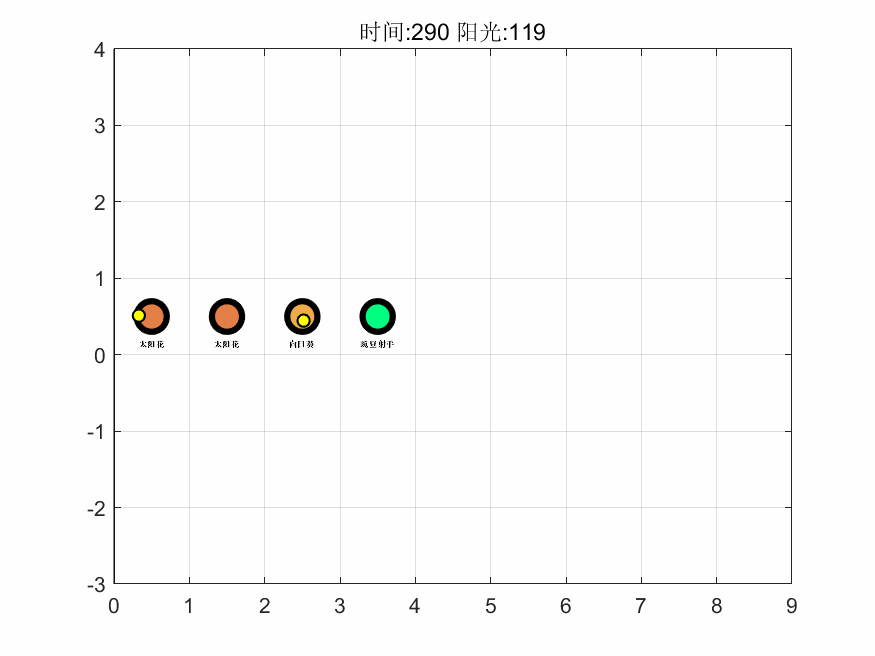
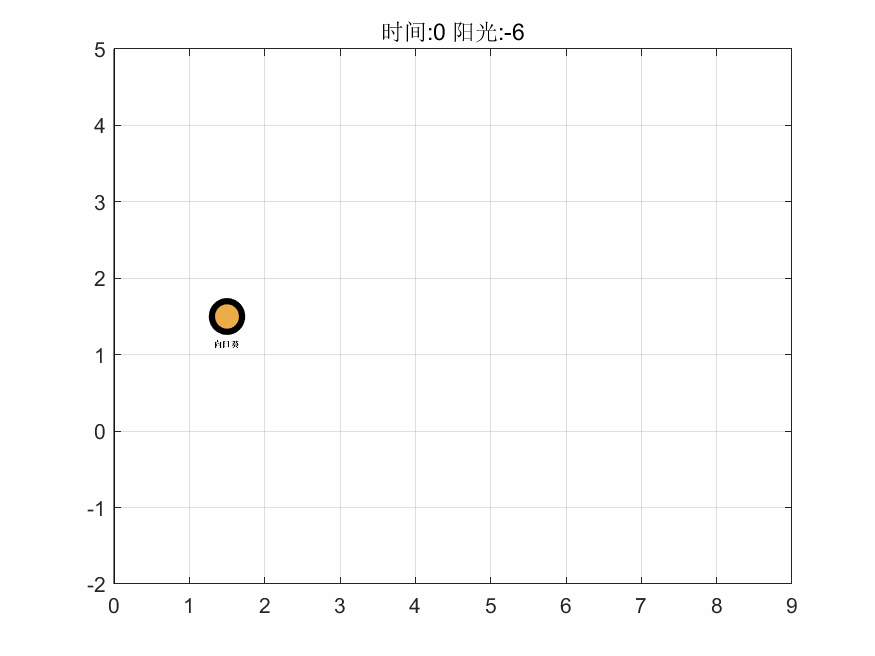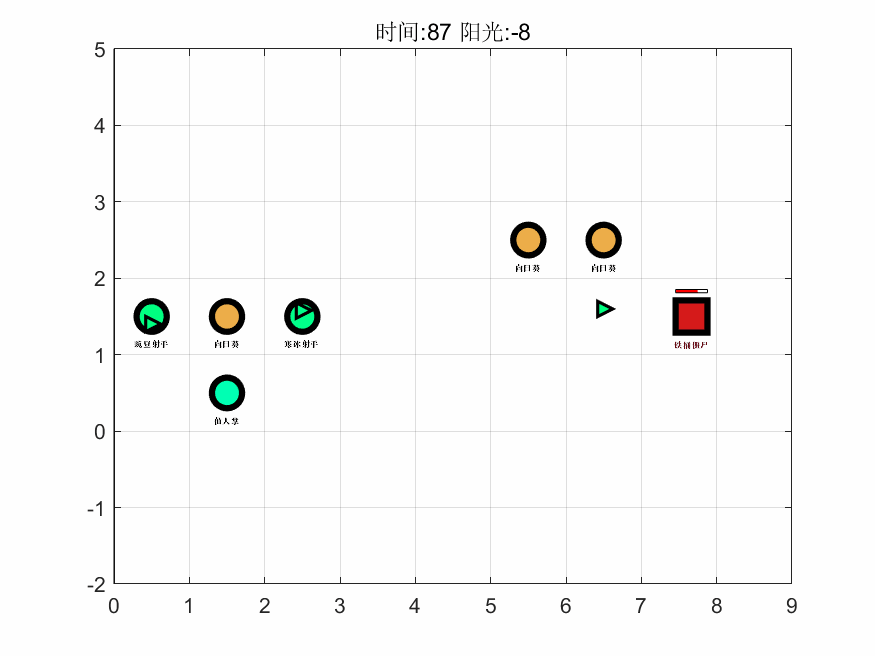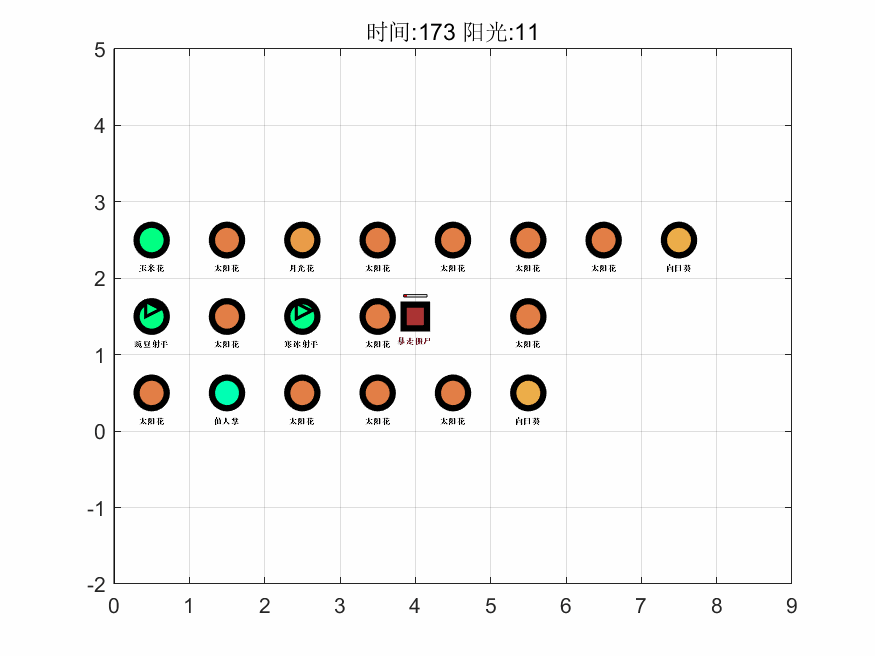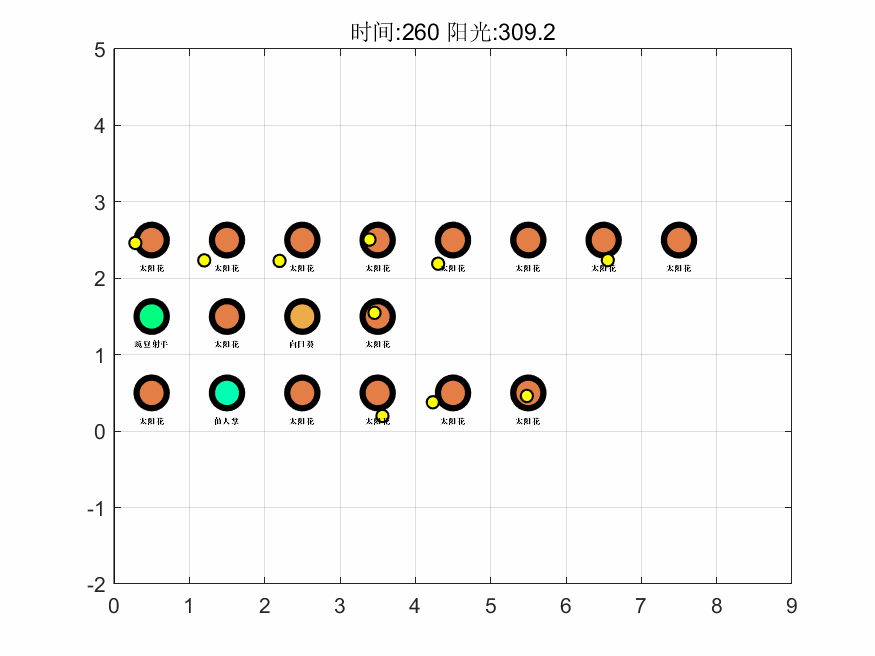
基于上述算法,在 MATLAB 中编程进行求解,得到第一关的最大阳光增量为 159,即游戏通关后保留阳光的最大数量为 165。接着,基于对最优解进行计算机模拟了整个过程,抽取其中 6 个时间点的可视化图像如下,完整的图集见支撑材料。
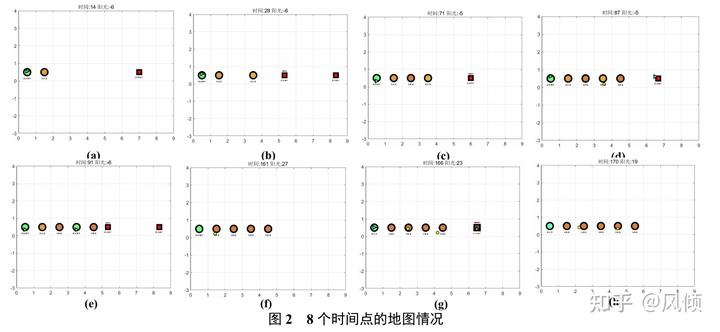
如图可以看出该解的思路为先以月光花、豌豆射手起手,在积累阳光的过程中渐渐将向日葵、月光花替换为生产效率最高的太阳花,进而使得生产量最大化,同时把攻击性植物替换且仅保留了一个仙人掌,而仙人掌最高的攻击力能使得每个僵尸最多移动三个,从而保护的所有植物。
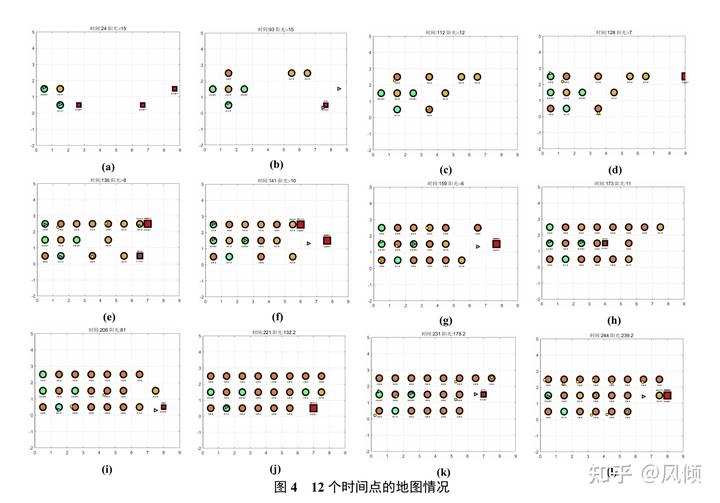
本题再次验证了前期发育的重要性,也同样出现了如同第二关之中的精彩操作,可 以共同验证法案的可行性和优劣。
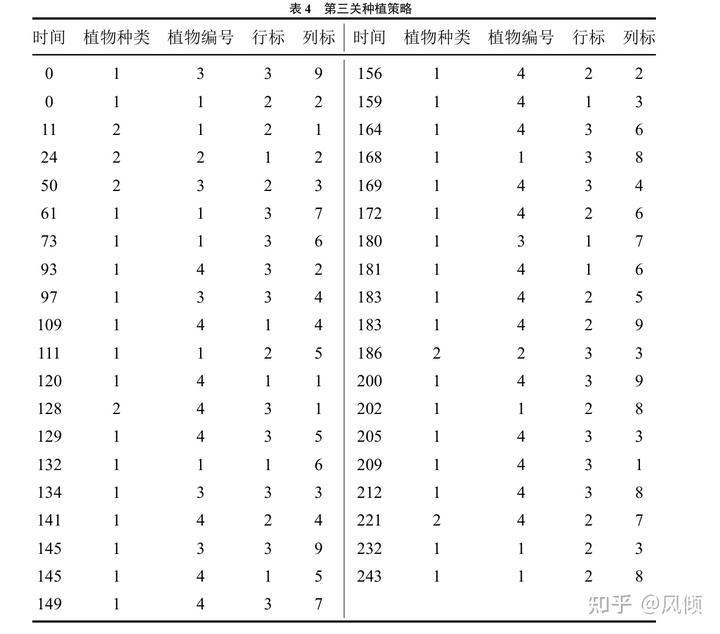
展示
ps:使用的植物和僵尸的数值和实际游戏中是不一样的,但是也可见一斑了。

 微信扫一扫
微信扫一扫 



