最强的公式,用起来绝对爽爆了
当
时,有:
(黎曼 zeta 函数)
(狄利克雷 beta 函数)
其中
其中
附:为了方便计算,我们需要知道
其中,
瞬间感觉其他的求和都弱爆了有木有!!
(拉马努金饶命)
维球体的体积:
由它可推出所有偶数维度的半径为
的球体体积之和为
————下面是应用————
以及, 1000 维球体的体积:

下面附上几个公式的证明
1.证明
令
,构造正方形围道:
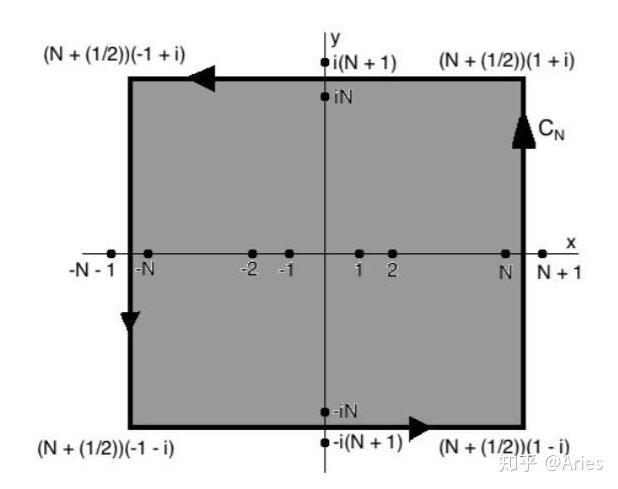
它在全平面的奇点是
,其中
为
级极点。
下面计算留数:
考虑到展开式:
,其中
为伯努利数
可以得到:
所以:
带回原式得:
由留数定理:
令
,上式变为:
解得:
2. 证明
它也可以用留数证,过程留做习题
下面我们换种方法证~
引理 1:
设:,则有:
,(
)
证明:
读者自证不难,留作习题。(提示:先求出)
引理 2:
若在
处
(
)阶可导,则有:
证明:
显然。(提示:泰勒展开)
取
它的根为
,(
)且均为二重根。
将
展开为无穷乘积:
而我们有:
由引理 1知
式左端等于:
由引理 2知
式右端等于:
此处利用了展开式:
综上可得:
实际上
也可用此方法哦~具体过程留做习题。
3. 证明当
时,有:
由Weierstrass 公式:
可得:
把
分别换成
带入
式,换成
带入
,然后相乘可得:
原式便是此式的特殊情况,即
用此式还能推出这类的无穷乘积:
这么多赞了!!不更一下都觉得不好意思!!!我就放几个积分吧~
(弱弱地说一句,我搞不懂的式子不敢放出来……)
这是一个很像泊松积分的东西。
……
若令
,可得到:
下面是一大串拉普拉斯(Laplace)积分的推广:
实际上,它有递推公式:
所以知道
后就能欢乐地推下去了~
抽空再更~o(≧v≦)o

 微信扫一扫
微信扫一扫 



