这个问题本来不指望有多少人能关注，因为太专业了，基本不是化学相关本科及以上的，可能连提问都看不懂... 但让我意外的是，有一大批专业大佬赶到现场支持点赞评论，真的很感谢。当然也提到了很多补充信息，我觉得很好，所有建设性的意见都在文中引用加上去了。也希望大家有不同意见或者补充意见的都在评论区指出，我有时间都会看，然后完善到回答里。

我看到这个问题还挺有意思的，因为很多教材都只是说结论，而没有分析其中的原因，当然不排除有好的教材会讲的很清晰，如果你知道，请在评论区告诉我是哪本教材。所以如果光看教材，有疑惑是很正常的。然后我看到知乎上居然没几个人回答类似的问题，如果知乎上没人答，百度知道更不会有人答了（手动狗头）。另外，我有点强迫症，想要纠正一下提问中的名词：是“偶极矩”，不是”偶极距“。

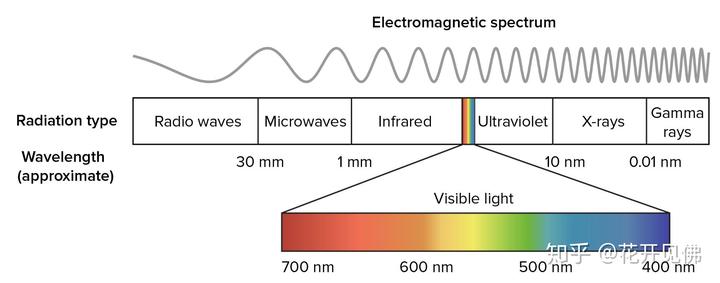
首先从大背景讲讲，就先说说光谱，物理学上讲电磁波就是来源于电荷的振荡，振荡的频率决定了电磁波能量高低，红外(Infra-red)实际上是电磁波一种（700 nm~ 1mm），它的吸收主要对应于分子的振动（vibration），比红外波长更长的是微波（microwave, 微波炉就用这个），微波主要对应的是分子的转动（rotation）,红外光谱其实经常和微波光谱连起来讲，因为振动光谱经常和转动光谱相耦合（Rotational–vibrational coupling）。比红外更长的就是无线电波（radiowave，也就是收音机能接受到频率的波长，一般是米级别的），这种电磁波，靠简单电路就能产生（振荡电路）。

然后再简单说说短波，比紫光波长更短的就是紫外了（ultraviolet），紫外波长的吸收对应的就不是原子核的振动和转动了，而是分子的价电子的跃迁了（或者你说电子在分子轨道中的跃迁也行），打过紫外光谱的同学都知道，紫外峰一般都很宽，这当然还是因为耦合，原子核运动和电子效应的耦合（vibronic coupling）。比紫外更短的波是X 光（X-ray），波长小于 10 nm，长于 0.01 nm。X 光对应的就是更高能量的电子跃迁了，是属于内核电子的跃迁。实验室常用的 PXRD 的 X 光波长是 1.5406 Å （Cu K alpha, 0.15406 nm）。如果对 X 射线要求比较高，可以做同步回旋 X 光（synchrotron X-ray）,11-BM 的波长大约是 0.46 nm。 伽马射线（Gamma rays）就更高能了，低于 0.01 nm 这种波长的光，基本上核爆时才能产生了。

@Childhood Chen，这个评论补充的很好哈，其实我对 Mössbauer 了解不多，只是组里有师姐拿 Mössbauer 测过铁离子的价态有听说过这个名词而已，不过我后来又查了些资料才知道伽马射线（γ rays)也可以用来测原子核的吸收光谱，对应的是原子核的能级跃迁。

gamma 射线谱图最常见的是 Mössbauer 谱，对应的是核能级的跃迁。

@渣渣龟提到了耦合作用对分子光谱复杂性的贡献：

分子光谱的复杂性，还包含有各种振动耦合，一般而言这种耦合产生的吸收谱很难用某一种单一模型来解释。比如在太赫兹频段内 vibrational 和 rotational 振动互相耦合会产生更加复杂且更加丰富的光谱信息。

这个大背景其实对于学光谱的同学来说是很重要的，你看下面一张光谱图就能把咱们学过的常见光谱仪器全串起来，除了无线电波（radiowave）和伽马射线（Gamma rays），下图中间四个波段的电磁波都对应着一种基本光谱仪器，微波光谱(Microwaves spec)，红外光谱(IR)，紫外可见光谱（UV-vis）,X 光衍射（X-ray）。

再讨论一下原子核运动的几种模式（如下图），从能量从高到低排序分别是：振动（vibration），转动（rotation）和平动（translation）。

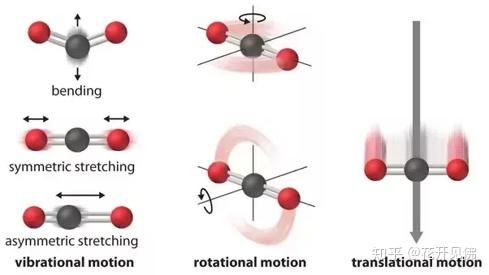
如果分子含有 N 个原子核，那么该分子原子核的波函数就是 3N 个坐标的方程（3 维空间）。除去 3 个平动自由度和 3 个转动自由度，一般分子的振动波函数是 3N-6 个坐标的方程（非线性，线性还要在此基础上减掉一个转动自由度）。那么这 3N-6 的坐标其实对应着 3N-6 种振动模式（normal modes）。

本来想把量子化学加简谐振动模型推导公式啥列出来装装逼，但是我太懒了，而且估计没几个人有兴趣，所以本回答就定义成科普贴了。你们想看公式的评论区找我或私信我，我把课件发给你们看。

大背景介绍的差不多了，回到主题，红外和拉曼光谱的吸收说白了都是偶极矩的变化，不过红外产生自分子固有偶极矩（permanent dipole）的变化而拉曼是诱导偶极矩（induced dipole）的变化。什么是诱导偶极矩呢？一会儿讲拉曼的时候介绍。

对于红外来讲，为什么说它的吸收是因为偶极矩的变化呢（别说不知道啥是偶极矩，请自行百度或教材），请看下面的图。

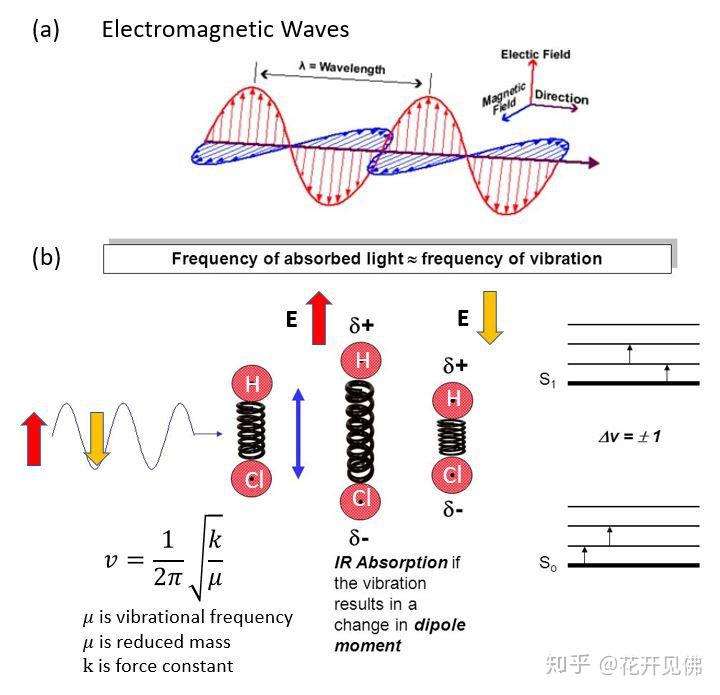
首先说说图 a，电磁波由相互正交的变化电场和变化磁场组成，当电磁波和分子作用时，分析红外我们只考虑电场效应，因为偶极矩是由分离的正负电荷组成，静态电荷只在电场中受力（运动电荷在磁场中受洛伦兹力，在本分析中不考虑）。由于电场方向在电磁波传播过程中是来回振荡的（向上或者向下，在图 b 中，向上的电场标记为红色箭头，向下的电场标记为黄色箭头），那么当向上的电场矢量接触到 HCl 分子时，偶极矩会受电场力而产生拉伸（不会分析你就把偶极矩拆开成正负电荷，分别来看，很简单）。同理向下的电场矢量接触到 HCl 时，偶极矩在电场下会被压缩，这样电磁波在一段时间持续辐射 HCl 分子的这段时间里，HCl 会吸收（IR absorption）电磁波的能量，持续振动而转化为振动能（vibrational energy）。偶极矩被压缩或拉伸之后（位置矢量改变），其大小都会发生变化，因为偶极矩的公式是：

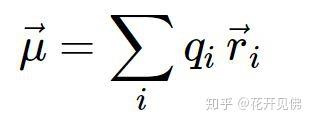
前面提到红外和拉曼的吸收都是因为偶极矩的变化，不过红外是因为固有偶极矩，而拉曼是因为诱导偶极矩变化。

固有偶极矩（Permanent dipole）：如下图中的水分子，对于极性分子，都会存在，由于电荷点乘位置矢量叠加后的总矢量不为零。

诱导偶极矩(Induced dipole)：如下图中的氧气分子在外电场下。不管极性非极性分子都存在，它同时也是范德华力的来源之一，产自外电场的诱导作用，导致电荷分离和产生的偶极矩。

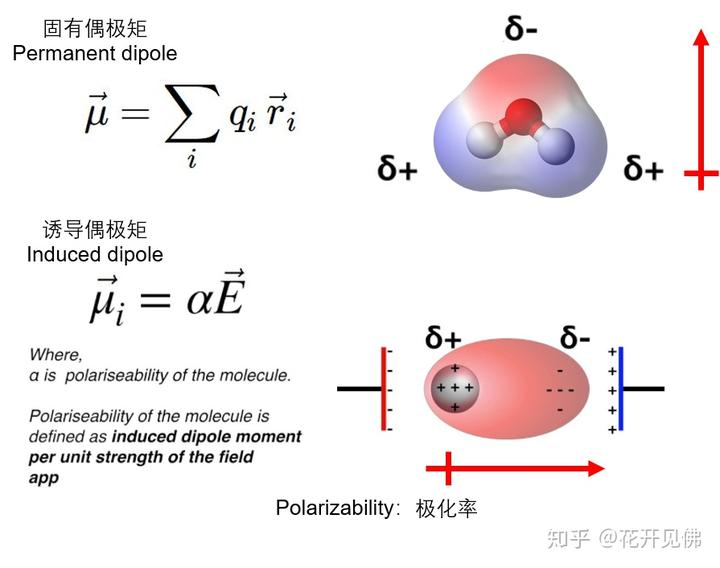
极化率（polarizability）：简单理解就是分子在外电场作用下产生变形（distortion）的能力。一般来说电子越多的分子，电子云分布越广，越容易产生形变，极化率越大。同时极化率也会随着分子的振动而变化（图五：甲烷的对称呼吸振动模式），因为电子云分布或者弥散程度改变了。诱导偶极矩和极化率成正比，极化率越大，诱导偶极矩也就越大。那么在外电场一定的情况下（拉曼的激发激光波长一定），要想要诱导偶极矩变化，那就需要极化率变化了。换而言之，只要极化率的变化率不为零，分子振动模式就是拉曼光谱可见的。翻译成数学语言就是极化率对于正则坐标（normal coordinate）的一阶导数不为零：

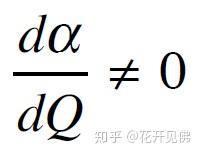
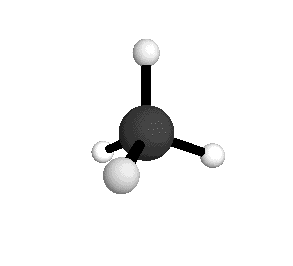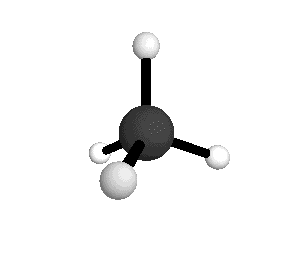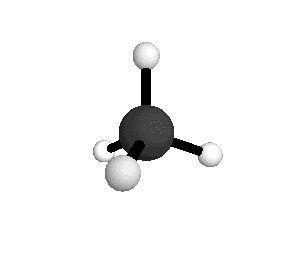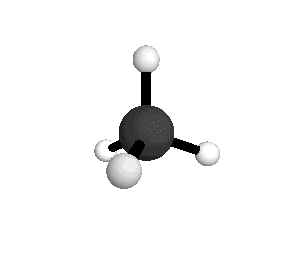
另外再举个例子，如下图，CO2 的拉伸振动模式有两种，一种是对称振动（symmetric stretch），一种是非对称振动(Antisymmetric stretch)。其中对称振动模式偶极矩变化为零（μ=0），极化率变化不为零（α≠0），所以红外不可见但拉曼可见，非对称振动刚好相反。

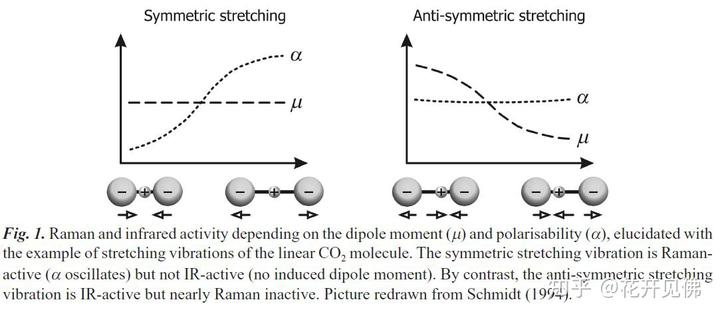
关于什么是正则模式（Normal Mode），正则模式就是一种分子内部的振动或者运动方式，红外可见的正则模式，偶极矩会改变。常温下，分子的热运动是一直在进行的，不管是平动转动和振动。只是说吸收红外能够把分子从基态振动能级激发到更高的激发态能级。就跟弹簧简谐振子一样，你给它一个初能量（相当于基态），它会一直以某个频率（激发态）振动，当然这是理想情况。真实情况下，分子吸收的红外能量会以各种各样的方式耗损，对于红外而言，除了激发分子的振动，大部分转化成了分子的热运动，即内能。关于正则模式，可以参考我另一个回答：

测红外时，一个基团在图上可以显示几个峰？比如一个 c=c 在图上能够显示几个峰？

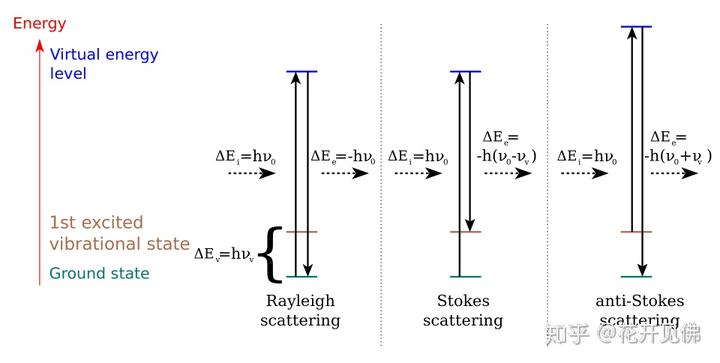
说到这里基本上这个问题算是完全解答完了。这里还想补充一些拉曼光谱的细节。不同于红外吸收，红外的光源当然是红外光啦，拉曼光谱的光源是可见光。是因为两种光谱的性质不同决定的，红外测的是吸收光，拉曼测的是散射光。值得一提的是，只有很少一部分激光会被散射掉（大约 1/1000，或者 1/10000），大部分激光会直接穿过样本。如下图，入射光被分子散射，有三种不同的结果：瑞利散射（散射光能量不改变，光子的弹性碰撞 elastic scattering），斯托克斯散射（散射光能量降低，非弹性散射 inelastic scattering），和反斯托克斯散射(散射光能量增加,非弹性散射)。

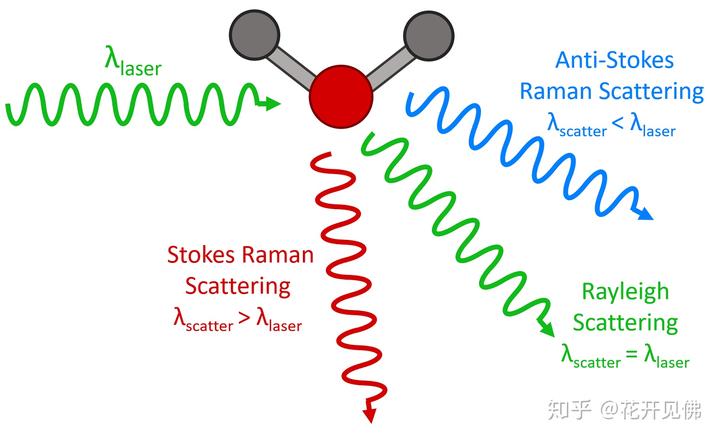
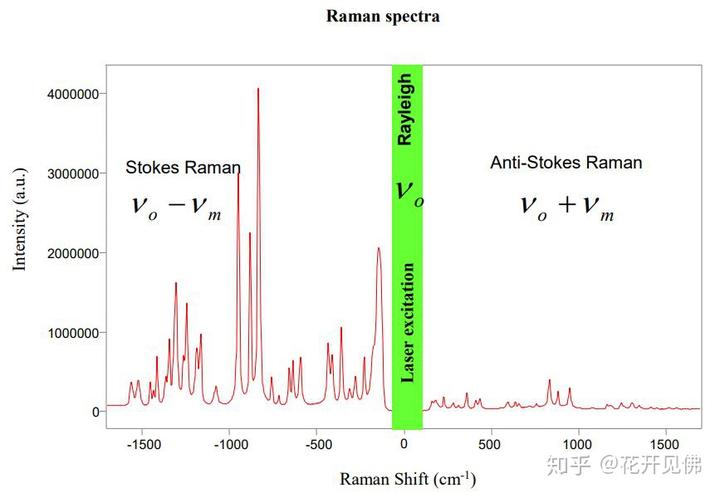
另外可以看看拉曼光谱长啥样：下图很清晰的展示了刚刚介绍的三种不同散射模式在实际图谱中的是什么样的。斯托克斯拉曼（Stokes Raman）能量比激光低，散射光强要远远高于能量比激光高的反斯托克斯拉曼（Anti-Stokes Raman）。很容易理解，因为能量穿过一堆分子时，被吸收一部分的可能性远远高于从分子那得到能量的可能性。就好像你给一群人 100 块钱，你隔两天再找他们要，你觉得是要到 10 块钱的可能性大，还是要到 200 块的可能性大？

@Triborg另外有评论说到（他自己肯定知道答案，应该是希望我补充）：

那么请问为什么拉曼谱的测量要在垂直入射光方向、而红外谱的测量要在入射光方向呢？

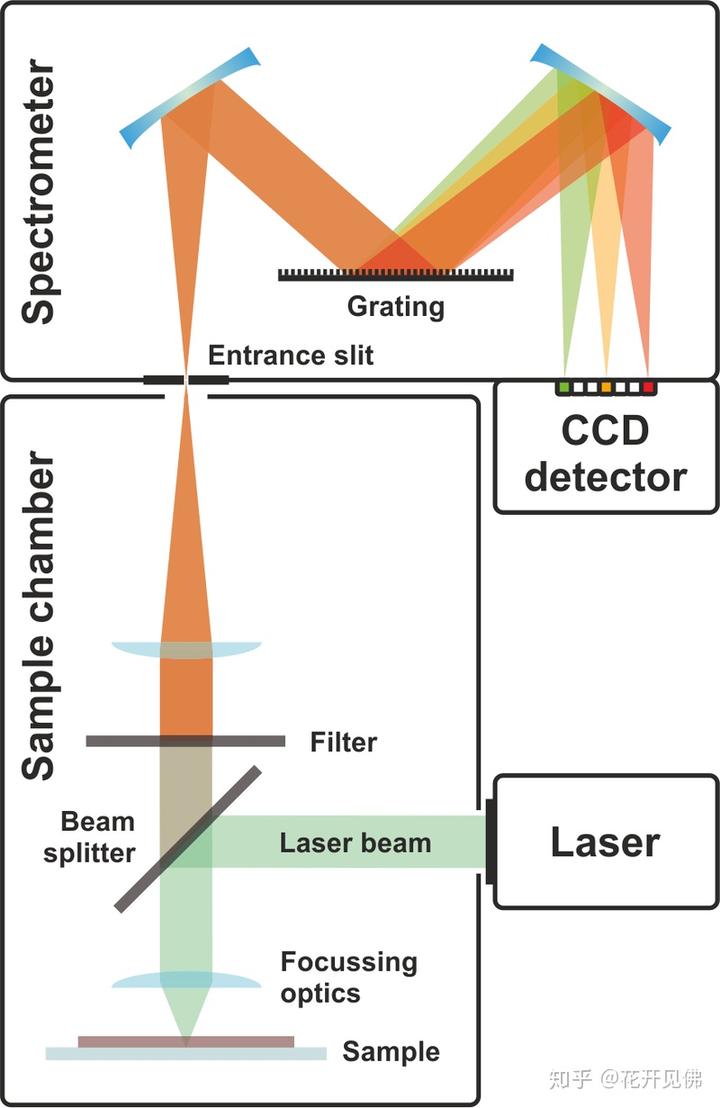
我的补充回答是：拉曼测的是可见激光散射（scattered light），所以垂直入射方向测量，这样探测到的被散射的光子数比较多（如下图 8）。而红外谱图测量是测的红外光吸收（light absorption），所以说希望光穿过 sample。

拉曼光谱的玩法千千万万，每年发的 paper 都一大堆，所以说 setup 的方式也很多样化，图中的只是其中一种 Raman 测法。

就像@William Zhang提到的，

我们有一门课让搭拉曼，就是测的入射方向的。后面用一个滤光片就可以了。不过从侧面测应该信噪比会高吧，荧光也是从侧面测的。

目前想到的就这么多了，之后再想到什么会在这里更新。之后可能会讲些拉曼光谱和红外光谱的优劣势和应用范围吧。

在私信里收到了@NOWADAYS 的以下问题，我本来想找到你的链接，但是可能你账户太新了，所以没有圈到。

1.从诱导偶极矩看，是外电场诱导极性或者非极性分子产生，我理解此处的“外电场”是指入射光带的外电场（光是电磁波），如果这样的话，红外光也是电磁波，也是带有“外电场”的，为何不会诱导极性或者非极性分子产生诱导偶极矩呢？

回答：红外光是电磁波，也带有外电场，讲道理说也能产生诱导偶极矩。但是分子中的电子轨道是量子化的，所以说你要使电子云产生极化而偏向某一边，势必要使分子中价电子产生跃迁（electronic transition）或者激发(excitation)到更高能量的轨道(higher virtual energy level)上去。我们之前在光谱介绍时说过了，想要激发分子中价电子，电磁波能量至少要是可见光和紫外光级别的能量，所以说我的解释是红外光频率不足以激发产生诱导偶极矩，即便有应该也很少。这个问题在@Luyao Zou的回答里也提到过。

2.为什么红外光与物质作用就是吸收而没有散射，而拉曼激光与物质作用就是散射而没有吸收呢？

回答：红外光主要是吸收，散射也有，但是很弱，还是因为红外光频率太低。拉曼一般用的是可见光激光，也会有吸收，取决于你的物质的种类。但是由于可见光频率较高，所以说散射概率增大。下图是瑞利散射光强和入射光波长之间的关系，基本规律是：波长越短，频率越高，散射光强越高。我还习惯从波粒二象性的角度理解，波长越短，光的粒子性越明显，越容易发生弹性散射，波长约长，光的波动性越明显，和物质作用越容易被吸收。

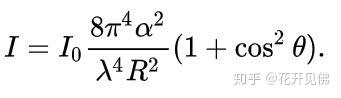
喜欢的同学们帮忙按个赞，你们的支持是我创作的最大动力，明天继续更新！

参考网站（Reference）：

1. https://en.wikipedia.org/wiki/Raman_spectroscopy#/media/File:Setup_Raman_Spectroscopy_adapted_from_Thomas_Schmid_and_Petra_Dariz_in_Heritage_2(2)_(2019)_1662-1683.png

2.https://www.rsc.org/membership/networking/interestgroups/mossbauerspect/intropart1.asp

3. Lutz Nasdala, David C. Smith, Reinhard Kaindl, Martin A. Ziemann, 2004. "Raman spectroscopy: Analytical perspectives in mineralogical research", Spectroscopic methods in mineralogy, Anton Beran, Eugen Libowitzky