因为如果取消马脚,现有的中国象棋也会就此消失。
这不是危言耸听!
这一切都源于——当马脚取消后,马的强度将直接翻倍!
(需要强调的是:这里所说的“翻倍”,并不是一个直观感受上的翻倍,而是可以量化的“翻倍”。具体如何量化,将在后文中详细展开。)
象棋每一次规则的改动都是为了增加棋手对局的趣味性以及观众的观赏性。而马脚的存在无疑增加了棋局的复杂性和不确定性。
从直观上讲,所有的策略类游戏,无论是棋类,亦或是如今风靡的 MOBA 类、FPS 类等,都是从某种程度上对于战争情景的模拟与仿真。

象棋是对于中国古代战争的模拟,其中包括了車(车兵)、马(骑兵)、炮(炮兵)、兵 / 卒(步兵)等——車、马、炮、兵的组合进攻,同时配合士相的防守,使得战争的复杂性得以体现。
并且,行棋的规则也可以体现出一些棋子本身蕴含的内在规律。例如,相走田,“田”即粮食,所谓“兵马未动粮草先行”,“相”对于“帅”的保护体现在对于后勤的保障;再例如,炮发挥威力需要炮架,而車横冲直撞、士伴随将帅左右。行棋的规则也是尽可能地反映出真实战争中的某种兵种的特征。
说到骑兵(马),其最为明显的特征在于它的机动性。或许有人会有所疑问,象棋中机动性最强的不是車吗?
的确如此,車在象棋世界中的机动性与威慑力的确是最强的。但是,在现实世界里,骑兵的机动性往往体现在长驱直入、直取敌将。
而在象棋中,这一点被体现得淋漓尽致。我们常称“車马炮”为象棋中的三个大子。马是唯一一个在单独进攻并且对方没有用大子布防的情况下,可以迫使对方将 / 帅易位的大子。而敌方的車、炮在单独进攻的情况下,都可以通过我方士相的阻隔,对于将 / 帅形成有效的保护。
在将帅在原位时,马能够直接攻击将帅的点,称为“卧槽”。卧槽马无法通过士相对将 / 帅进行保护。
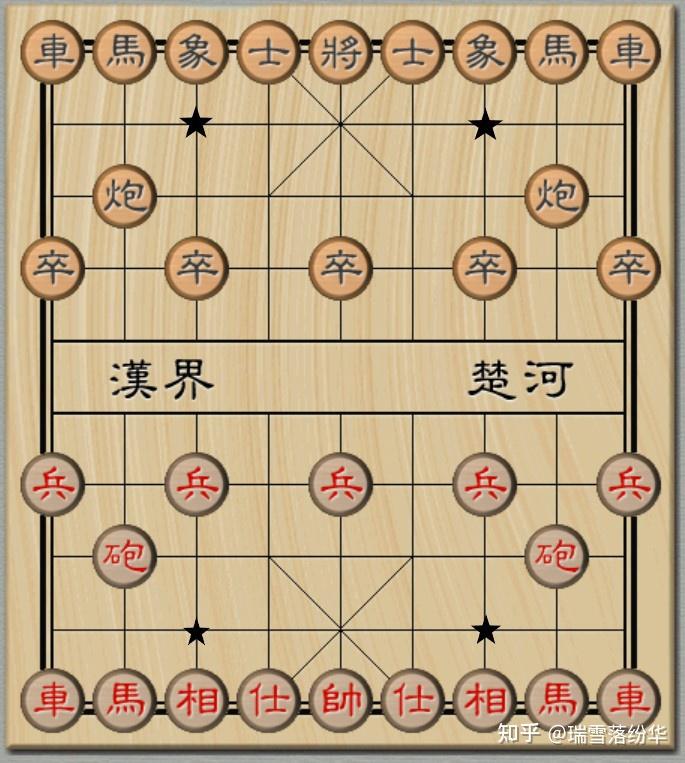
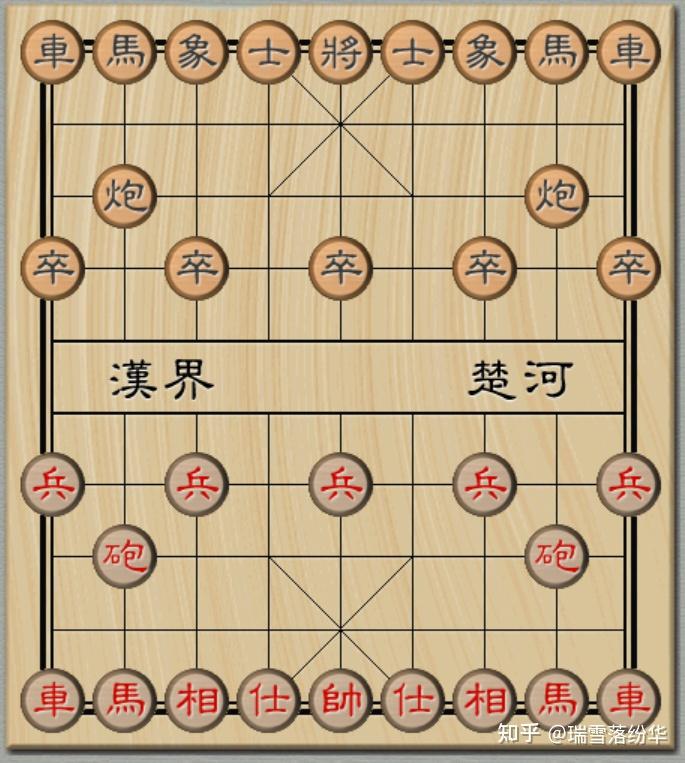
以如图所示的实战为例。红方的車、炮尚未过河,而马(骑兵)孤军长驱直入,已然威胁到黑将。
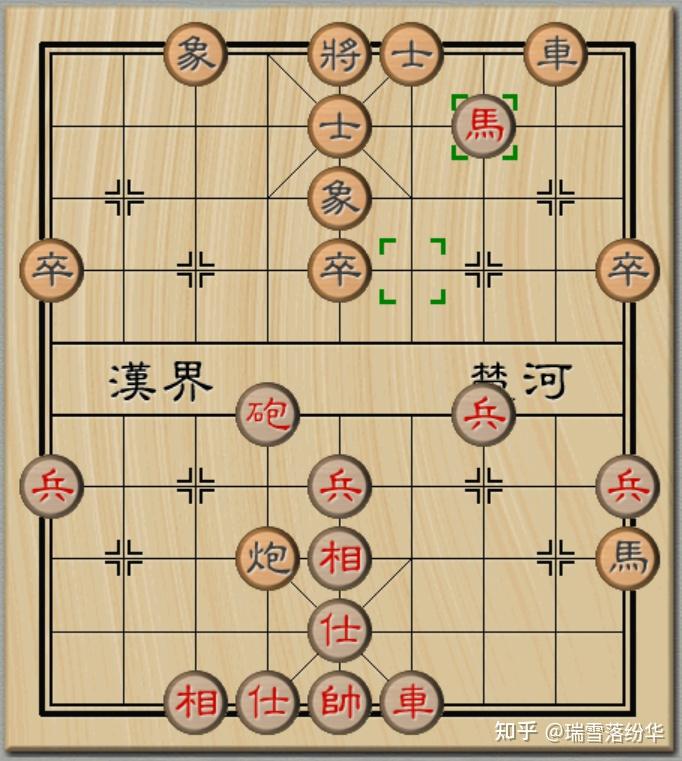
此时,红马跳槽叫将,黑将只有出将(或者说易位),有且仅有这一个选择。
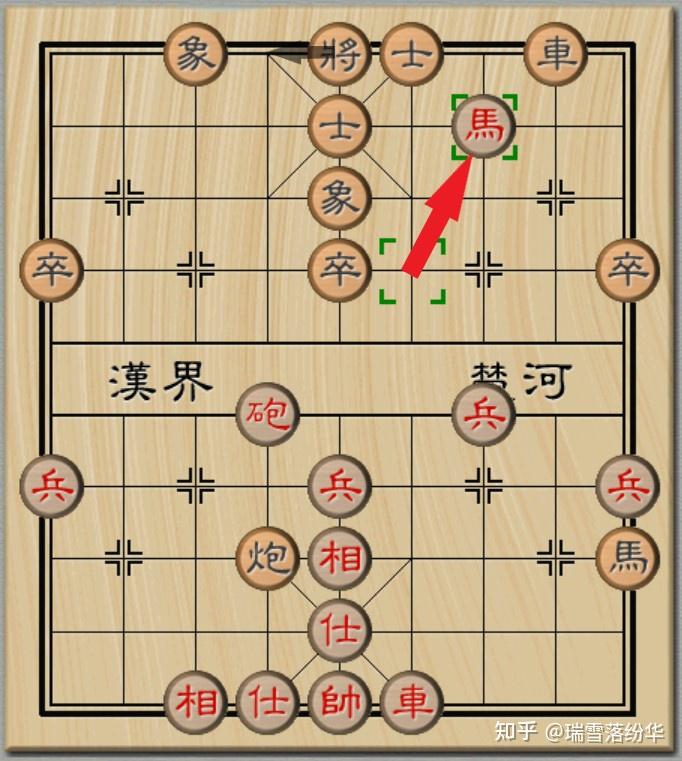
黑方士相虽然严阵以待,看似固若金汤,但是对于马的攻击无法起到有效的保护。马在进攻端的威力已经不言而喻。
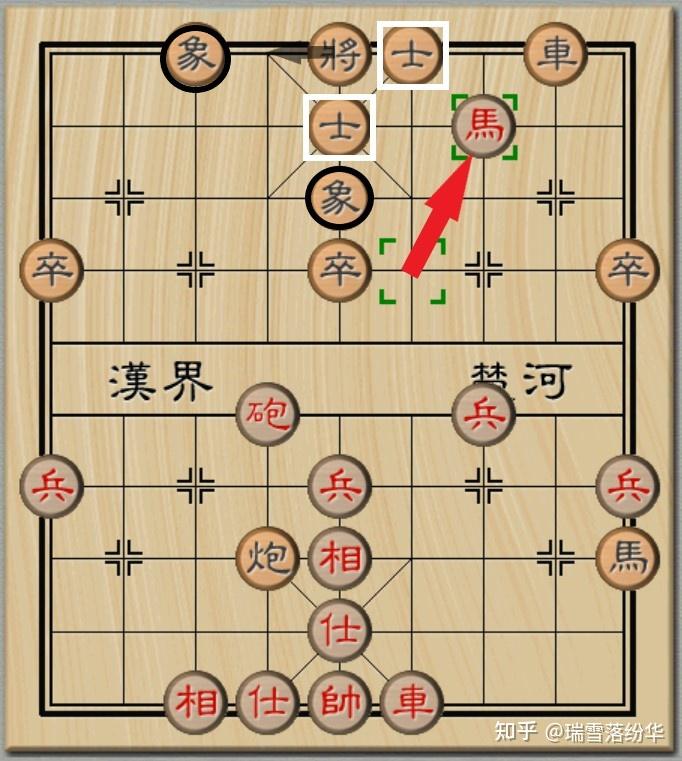
试想,如果象棋中没有设置马脚,马对于将帅的攻击力将大大增加。除非提前布置大子对于马预计的进攻路线进行布防,否则用马叫将,将 / 帅就要易位。一旦将 / 帅易位,士相对于将帅的保护作用就会显著降低,从而使得車炮的进攻也得到极大地提升。
而在防守中,马的作用也不可忽视。以正马为例,图中的①②可以对中卒和边卒形成保护,尤其是防守敌方炮的进攻;③④主要是防守敌方“炮击底士”“大刀剜心”等凶悍的招法;⑤⑥则是可以防守敌方車、炮以各种途径下底,对将 / 帅产生威胁。
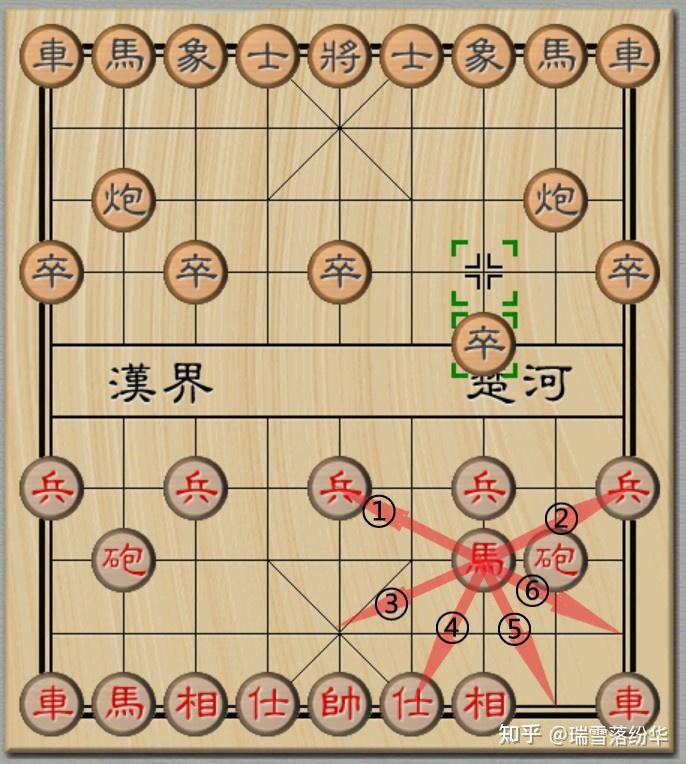
通过上述的两个例子,不难得出一点结论:即使是在当前有马脚限制的情况下,马在单侧的攻防都有其非常强势的表现。
可能有人会反驳,仅仅只是少数情况下,马的作用会显著增加,那么开局和中局阶段,马是否也会变强很多呢?
答案是肯定的。
开局阶段,最显著的特点是出子速度会变得极快——马可以三步直取对方中卒。
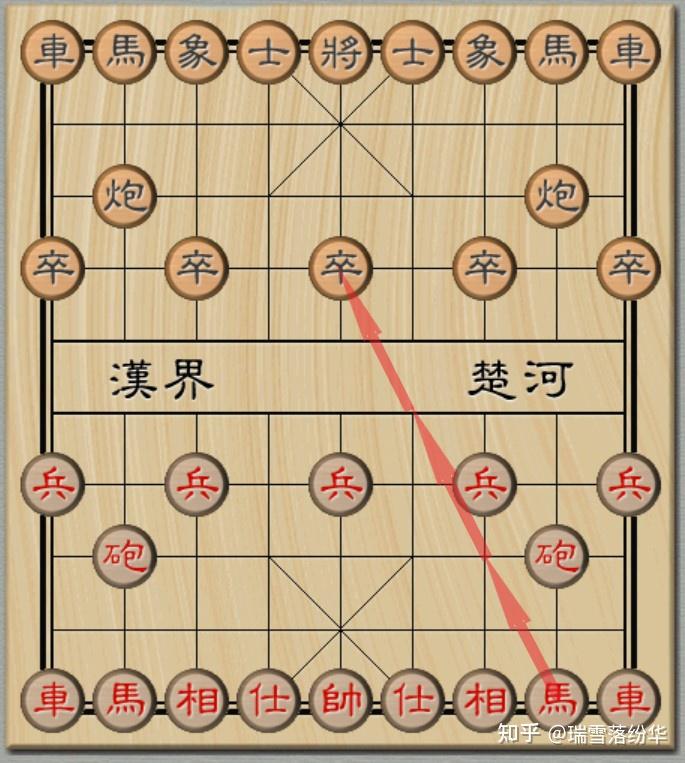
在正常的象棋规则中,开局以炮换马会使得红方“失先”。然而,在无马脚限制的情况下,红方第一步以炮换马会极大强化先手方的优势。因此为了平衡先后手,必须对开局以炮换马加以限制。方案一是禁止开局以炮换马;方案二是通过改变棋子的初始位置,用以规避以炮换马。
中局阶段是最为复杂的。因此在阐述中局阶段马的攻击力必须引入两个概念:子力固定价值和子力实际价值。
在此之前,首先介绍一下子力价值。
作为象棋爱好者,对于子力价值一定都不陌生。一般来说,子力价值是用来评估局势以及在兑子过程中衡量盈亏的方式。具体的子力价值如下:
| 車 | 炮 | 马 | 士 / 相 | 兵 / 卒(已过河) | 兵 / 卒(未过河) | |
|---|---|---|---|---|---|---|
| 子力价值 | 9 | 4.5 | 4 | 2 | 2 | 1 |
我们常说的子力价值,也可以称为子力固定价值。
子力价值自上而下呈现出金字塔结构,服从大多数团队的组成架构。
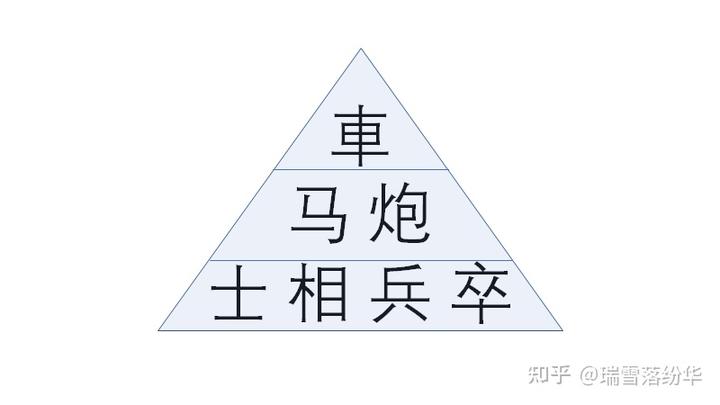
同时,子力价值越大的棋子,距离棋盘中心越远。(这一点非常重要!)
子力固定价值是如何计算的呢?用统计的语言来说,某个子的子力固定价值是某个子所能攻击 / 控制的点数的数学期望。当然,具体的结果并不需要那么精确,大致量化表示每个子的攻击范围即可。
所以,在实际的计算过程中,除了未过河的兵 / 卒外,
子力固定价值=攻击 / 控制点数的数学期望≈攻击 / 控制点数的最大值➗2
未过河的兵 / 卒所能控制的点数的最大值即为其数学期望,因此对于未过河的兵 / 卒来说,
子力固定价值=攻击 / 控制点数的数学期望=攻击 / 控制点数的最大值
具体的每个子的攻击 / 控制点数的最大值如下:
| 車 | 马 | 士 / 相 | 兵 / 卒(已过河) | 兵 / 卒(未过河) | |
|---|---|---|---|---|---|
| 攻击 / 控制点数 | 17 | 8 | 4 | 3 | 1 |
棋盘奉上,便于大家心算验证。
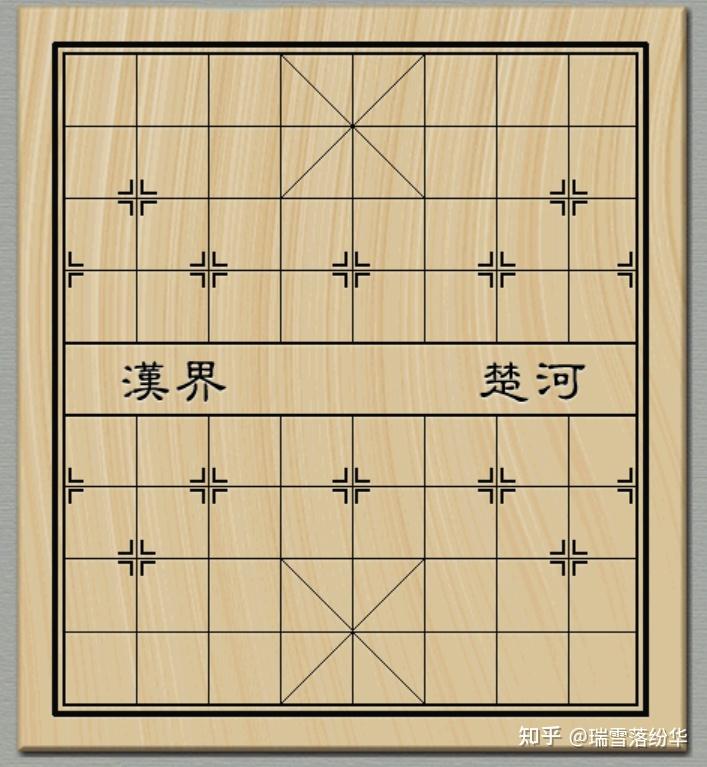
車和已过河的兵 / 卒向上取整,分别为 9 和 2;马、士 / 相分别为 4 和 2。
由于在实战中双炮共同作用时,能够产生类似于車的效果,因此炮的子力固定价值取車的一半,即 4.5。
而子力的实际价值并不等于子力固定价值。子力实际价值表示其实际控制的点数,所以子力实际价值并不是一成不变的,而是动态的,与其所在的位置以及和周围的棋子位置关系有关。
这也就是为什么要快速出动大子。因为大子在其初始位置上的实际子力价值是很低的,而当車无论是平一还是进一,子力的实际价值瞬间会增大很多。
象棋中还有車路要通畅,要避免低头車等等原则,都是在告诫我们行棋时应当注意最大化子力实际价值。
为什么最大值除以 2 即可以视为控制点数的数学期望呢?
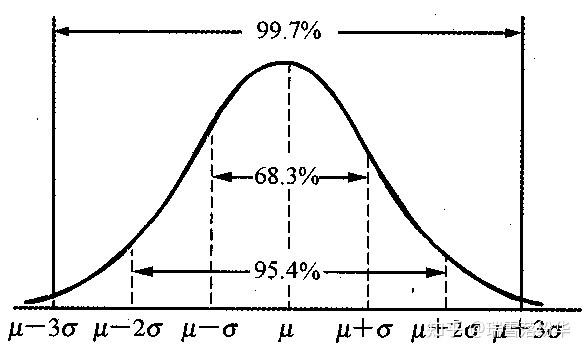
因为无论哪个大子在实战过程中都很难发挥出子力的最大值,因为象棋并不是比较哪一方的子力价值更大哪一方获胜,而是哪一方能够形成绝杀哪一方获胜。
在实战过程中,子力的实际价值会在子力的最大值与最小值之间,呈现近似正态分布。所以,为了便于计算和快速看清局势,我们以这种方式为不同的棋子“明码标价”,将这个平均值,即子力固定价值,视为多数情况下的子力实际价值。
而当象棋取消马脚之后,我们再一次计算马的子力固定价值时,不难发现,在无马脚约束的情况下,马在大多数情况下的子力实际价值为 8,在少数情况下会变为 4 或 2。然而因为无马脚的约束,马一般不会跳到将自己子力实际价值降为 4 或者 2 的情况。因此,马的子力固定价值会接近于 8。相较于原来的子力固定价值为 4,这是极大地提升。
正因如此,由于马的子力固定价值的提升,防守子力价值不变,使得攻防子力价值的不平衡。而子力价值的“金字塔结构”也会打破。
与此同时,根据“子力价值越大,距离棋盘中心越远”的原则,当車、马的子力价值接近时,马的位置也会和車产生冲突。并且,考虑到开局以炮换马的情况存在,现有棋盘上的马的初始位置必须更换。
并且,即便马位不发生变化,现有的丰富的、宛如瑰宝的大量棋谱也将随着马脚的取消一同消散。比方说,“一马换双相”等弃子搏杀的战术会变少,甚至连最为经典的“中炮过河車对屏风马互进三兵”的布局谱招也将不复存在。
棋子位置变化、棋谱不再有价值,如此象棋,自然失去了其本来的意义。
其实自古以来,人们都在探索如何丰富象棋的玩法,例如似乎已经失传的三人象棋。
有的人希望将记忆力融入象棋中,于是创造了棋谱和盲棋。
有的人希望象棋也存在准确度与速度间的取舍,于是对象棋的时间加以限制。
有的人希望依托象棋的棋子产生新的游戏,例如,如今的揭棋、翻翻棋等,就像同样是扑克牌,可以演变出无数种玩法。
或许取消马脚会产生一种新的玩法,但这种玩法再也不是象棋本身。

 微信扫一扫
微信扫一扫 



