这个问题提得真的不错啊。
看到这个问题我首先想到是前段时间在知乎名噪一时的『诺顿穹顶问题[1][2]』。从个人角度来说,从题主的问题思路延伸下去,就自然地走向诺顿穹顶问题了。
实际上,从经典物理学,或者说是牛顿力学的角度来看,为了描述自然界的宏观物体的运动,首先我们需要引入一个二阶微分方程(牛顿第二定律)。这实际上意味着当我们假定物体的质量、初始位置与初始速度为已知量,则从施加于物体的外力,可以应用牛顿第二定律来计算出物体在其运动轨迹的任意时间的位置与速度。
换句话说,对于牛顿力学来说,时间本质上只是描述运动过程的一个参量,而并不指示所谓的『过去』和『未来』的信息,题主所谓的『时间 t0 右侧的信息,也就是系统的输入有未来的值』实际上已经在给定初状态时就已经确定了。在这样的假设下,实际上左导数和右导数没有区别,因为都是在初状态确定后,便都同时确定了。
就像我们提前录制好的视频(更确切的说法应该是 gif)一样,当视频拍摄完成后,视频下方的进度条虽然也有时间的单位,也在描述视频内事件发生的前后顺序,但在我们打开视频这个瞬间,这个视频内部的所有内容就早已经发生过了。这时,朋友来给你剧透只是单纯他想破坏你的观影体验,而不会因为从视频进度条的下游向进度条的上游传递消息而违背因果律。

但是,在牛顿力学当中,如果我们给定了初状态,体系之后的状态真的可以完全地被确定下来吗?实则不然。物理上我们可以直觉地认为所研究的函数性质足够『良好』,可以忽略很多其它的问题。但从数学上来说,想要确保初值问题存在唯一解,我们所研究的函数不仅仅要保证一致连续,还需要满足Lipschitz 条件,即函数图像上任意两点之间连线的斜率有界,才能真正确保初值问题存在唯一解。否则,就会出现诺顿穹顶这一悖论。
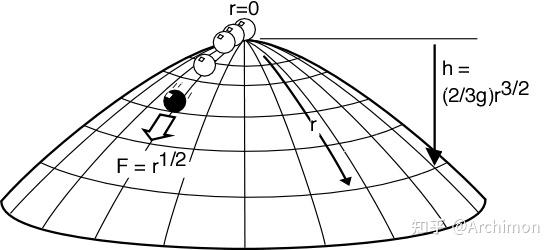
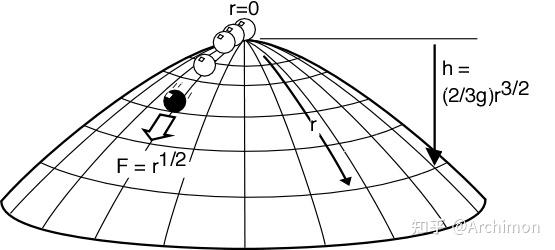
在 Norton 的圆顶模型中,质点 P 位于圆顶 D 的顶点 A,并且在 t=0 时刻处于静止状态。圆顶 D 的表面方程可以通过以下方式给出:
其中,
是圆顶表面上某点的高度,
是从顶点 A 到该点的距离,g 是重力加速度。
根据牛顿第二定律,质点 P 的运动方程如下:
只考虑 P 点的重力作用时,作用在质点 P 上的力 F 只有重力分量,其大小为 mg,方向向下。重力在圆顶表面切线方向可以表示为:
因此,质点的运动方程可以写为:
这个非线性的二阶微分方程有两个解:
1. 质点始终保持静止,即:
2. 质点开始滑动的非平凡解(non-trivial solution):
这里的 T 是一个未确定的时间,它代表了质点开始滑动的瞬间。这个非平凡解表明,在一定的初始条件下,即使没有初始扰动,质点可能会自发地开始运动。这一案例展示了经典力学中的一个非确定性例子,其中质点的未来行为不是唯一确定的。

 微信扫一扫
微信扫一扫 



