有意思的问题。
电子线路中有电路,配电网中也有电路,连普普通通的手电筒中也有电路。既然如此,我就对电容在电路中的运用铺开来谈吧,不局限在小小的比赛模型中。
电容的定义是:电量与电压之比。也即:
。
我们还知道,电阻是电压与电流之比,也即:
。那么电容与电阻的乘积是什么?我们来推导看看:
,我们把它叫做式 1
式 1 中,电容与电阻的乘积是时间,我们把它叫做电路的时间常数
。
流过电容的电流与电容两端的电压有如下关系:
,我们把它叫做式 2
再看容抗的表达式:
,我们把它叫做式 3
我们看到,频率 f 越高,容抗就越小。
再看电容与电阻组合后电容上的电压变化:
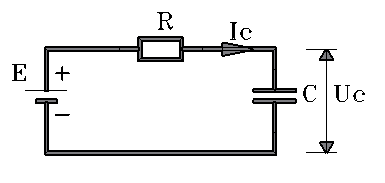
,我们把它叫做式 4
注意:
当
时,Uc=0;
时,Uc=0.6321E;
时,Uc=0.8647E;
时,Uc=0.9502E;
时,Uc=0.9817E;当
时,Uc=0.9933E。一般认为,当
时,充电或者放电就结束了。
如果电容处于零输入状态,则有:
,我们看到电容在放电。我们把它叫做式 5
有了这些基本知识,我们就可以来讨论电容在电路中的作用了。
第一个作用:隔直流
所谓隔离直流,其实就是高通滤波器的功能。这里的高通,指的是高频信号能通过,而低频信号较难通过,直流完全通不过。
这一点,可由式 3 看出来:频率越低,容抗越大;反之,频率越高,容抗越小,其实就是高通滤波器。
注意这里的电路条件:电容在前,负载电阻在后。由式 2,电阻上的电压为:
注意到这里出现了 RC 时间常数,它会产生何种影响?
第二个作用:无功补偿
我们知道,电感的电流滞后于电压,而电容的电流超期于电压。这一点从式 2 看出来。
设电压
,把它代入到式 2 中:
,电流变成余弦函数。当 t=0 时,正弦值为零,而余弦值为 1,因此当电压为零时,电流却取最大值,故知流过电容的电流超前电压 90 度。
在配电系统中,负载一般都是感性负载,造成系统中的电流落后于电压,产生了无功功率。所以,配电系统中往往要配套并联一些补偿电容,以期提高系统功率因数,降低电流滞后于电压的程度。
电容的这种用途叫做补偿无功功率补偿。
第三个作用:滤波
滤波体现了电容对信号的积分作用。
滤波电容如何设计?很简单的。假定某稳压电源的输出电压是 12V,电流是 2A,把 12 除以 2 得到 6,也就是说负载电阻近似为 6 欧。
当负载发生变化时,我们期望稳压电源的输出电压基本不变。我们取 5 倍时间常数为 100 毫秒,于是有:
取用标称容量 3300 微法的滤波电容即可。不过,此电容的耐压要取够。
往往在滤波电容旁边还会并联一个 0.01 微法的电容,它的用途是消除高频干扰信号。
第四个作用:用于构建振荡器
振荡器,我们不陌生,例如正弦波振荡器、方波振荡器、锯齿波振荡器等等。这些振荡器的结构元件中都离不开电容。
第五个作用:储存电能
据说,已经已经有用高能电容储能方式驱动的电动汽车。
第六个作用:建立移相电源
对于单相电动机,它有两组绕组。其中一组用单相交流电压,另一组则使用从单相电源串接电容后得到的移相电压,这样电机绕组才能对转子产生旋转磁场。
第七个作用:降压
利用电容的容抗来降压,这在充电器中使用得很普遍。
=================
下图是收音机电路,我们来看其中的电容有何作用:
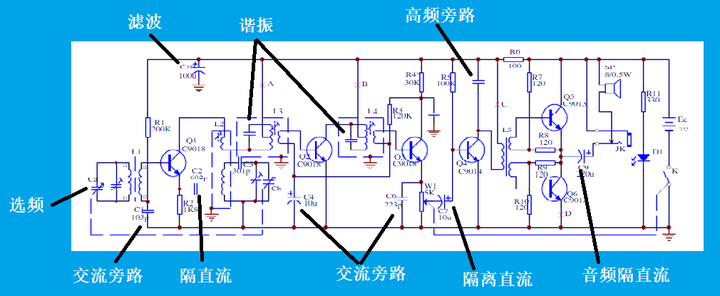
原理是什么?
再来看下图:
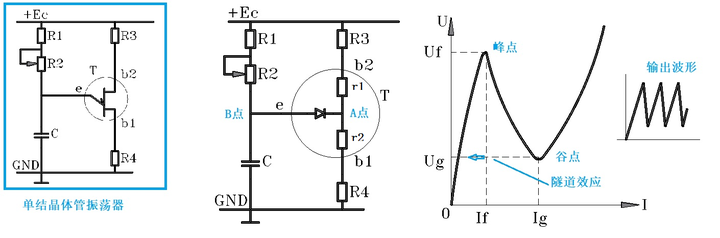
这是运用很广的单结晶体管振荡器电路,其中只有一个电容。我们来看看它起到何种作用:
由中间的等效图,我们看到电容 C 的电压为零时,二极管是截止的。于是电容 C 就通过电阻 R1 和 R2 进行充电。注意到 B 点的电压就是电容上的电压,为:
。
我们再看 A 点的电压:
这里的
是单结晶体管的分压比。
从伏安特性曲线上,我们看到电压从零开始沿着曲线上升。当曲线到达峰值点时,有:
,于是二极管导通,曲线瞬间下落。
有趣的是此时的电容,它通过二极管向 R4 放电,而 R1 和 R2 的电流也经过二极管流向 R4,于是 R4 上的电流大增。
当电容放电结束后,二极管截止,曲线瞬间从谷点向左切换到电容充电曲线中,这种效应叫做隧道效应。于是电容的充电又开始,电路进入新的循环。
电路的振荡波形见右边的波形图,振荡的主周期时间近似等于电容充电时间,由此可以求得振荡周期,为:
在这里,电容 C 的充电起到很关键的作用。
通过这两个例子,我们看到电路中的电容不是随意设置的,而是有它的道理在里面。因此,在探讨电路中的电容时,一定要结合原理来理解才好。

 微信扫一扫
微信扫一扫 



