更新了一下，把公式重新码了一遍，并且加上了图。
不是椭圆，把
泰勒展开
略去高阶小量，带入方程得到
这是一个倾斜的椭圆，和题主画出来图的很接近。因此原函数图像和椭圆差了一个高阶小量。
图来了
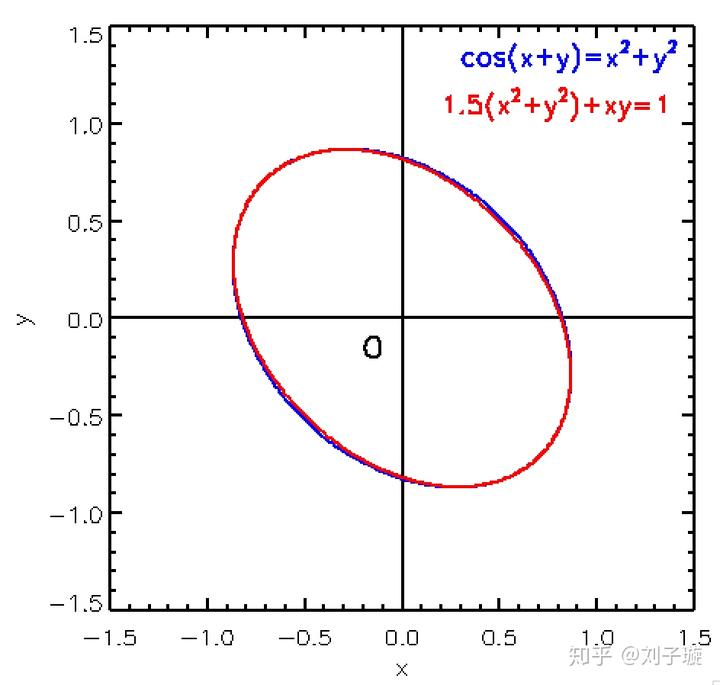
可以看到，两个图像还是非常接近的，基本重合了。
既然有不少人看，那我再补充一下怎么证明
是一个椭圆方程吧。
首先我们来理解一下坐标系的旋转变换，假设两个坐标系夹角为
，同一个点
在这两个坐标系中的坐标为
和
，再假设
和
轴夹角为
，那么我们知道：
而
和
轴的夹角为
，因此：
我们就得到了坐标的旋转变换。
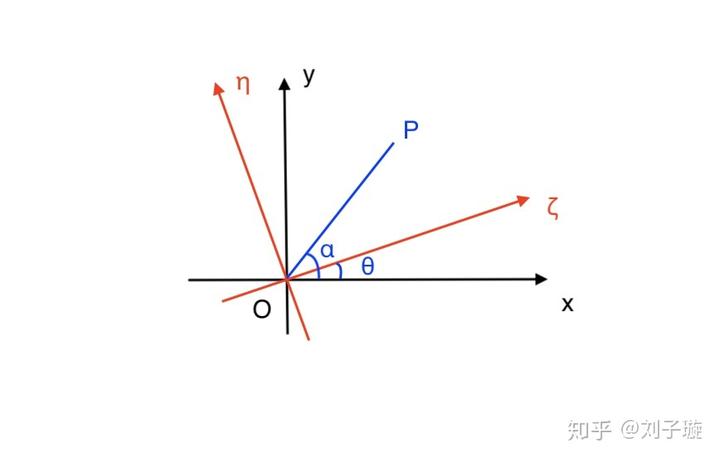
我们知道，标准椭圆方程是没有
项的，那么我们可以通过旋转变换来消去
项吗，答案是肯定的。如果令
，那么：
代入原方程
，我们得到旋转变换之后的方程：
这是一个半长轴为
，半短轴为
的椭圆的标准方程。因此原来的方程是一个旋转了
的椭圆方程。
1、关闭蓝牙。现在已经很少有人用蓝牙传输文件了，而且iPhone与安卓的蓝牙并不兼容，所以，可以在设置中，关闭蓝牙功能。2、关闭通知功能。关于APP推送，无非也就是一些更新提醒，关了也不会有什么影响，还能多省点电。3、关闭自动调节亮度功能。一般来说，可以将屏幕亮度在15%-30%之间，在强光环境中，在进行手动调整就可以了。4、禁止后台刷新。在设置—通用中，关闭后台自动刷新功能，也可以对省电起到一点...
1、点击高德地图APP界面底部的“导航”按钮，进入导航模式。2、点击右下角的“路线”，进入路线设定页面，根据要求输入起点、终点进行路线规划。3、点击“添加途经点”，弹出添加途经点页面，点击右上角，可以添加或者删除途经点，乘客可以手动输入要添加的途经点。4、当添加完途经点时，点击“确定”按钮，即可添加途经路线。此时地图会显示出这条路线上所有的途经点，以及当前途经点的地点信息。怎么设计高德地图设置要经...
您好，1.运动学-位移、速度、加速度的概念及计算方法-相关运动的分析方法，如相对运动和抛体运动-牛顿运动定律及其应用2.力学-力的概念及种类，如重力、弹力、摩擦力等-牛顿第一、二、三定律及其应用-力的合成与分解-能量、功、动能定理、功率的概念及计算方法-动量、冲量定理及其应用3.热学-温度、热量、热能的概念及计量单位-热传递的方式及其特点，如传导、对流、辐射-热力学第一、二定律及其应用，如热机效率...
十七世纪，整个科学界最重要的课题就是研究物理学尤其是天文学，微积分的概念也是由此诞生的。当然，当时研究物理学可不是为了像现在高中生一样，去计算万能小滑块的各种运动数值。当时的宗教普遍认为上帝处于“天堂...
鉴于许多答主已经回答过，周人的分封实际上是一种武装殖民策略，让诸侯带领商、周混合人群前往各地建国，并就地统治。那么我们不妨将这个问题变化为——周王朝对其分封的诸侯国控制力如何？这样的控制力是否可以称之...
微信扫一扫 
