广义相对论场方程看上去很简洁，但是实际上这个方程到底有多复杂？_网络百科

(很多谢各位捧场，既然有这么多知友捧场，我不更新一下写多点东西就对不起大家了）

这个，只能用太太太复杂了来形容了。真是太太太太复杂了。

爱因斯坦引力场方程的未知函数最多时可以有 15 个，其中度规共有 10 个未知分量，物质的能量动量张量有密度、压强和三个三维速度分量共有 5 个未知函数，所以共有 15 个未知函数。但场方程本身只给出 6 条独立方程，因为毕安基恒等式天然成立，它消去了 4 条方程。但毕安基恒等式使得爱因斯坦张量的协变散度天然为 0，所以场源的能量动量张量的协变散度也应为 0 又可给出 4 条独立方程，所以最后还是会有 10 条独立方程。但是，我们现在有 15 个未知函数呀，还差 5 条方程呢。这时我们需要引入谐和坐标条件，这个谐和坐标条件又可以给出 4 条独立方程。但还是差一条，所以还需引入一条新的方程：物态方程，这个物态方程原则上是由量子场论和热力学决定的，以表征物质本身的特性。下面是场方程的全景图（这个全景图是为答谢各位朋友的捧场而新增的）：

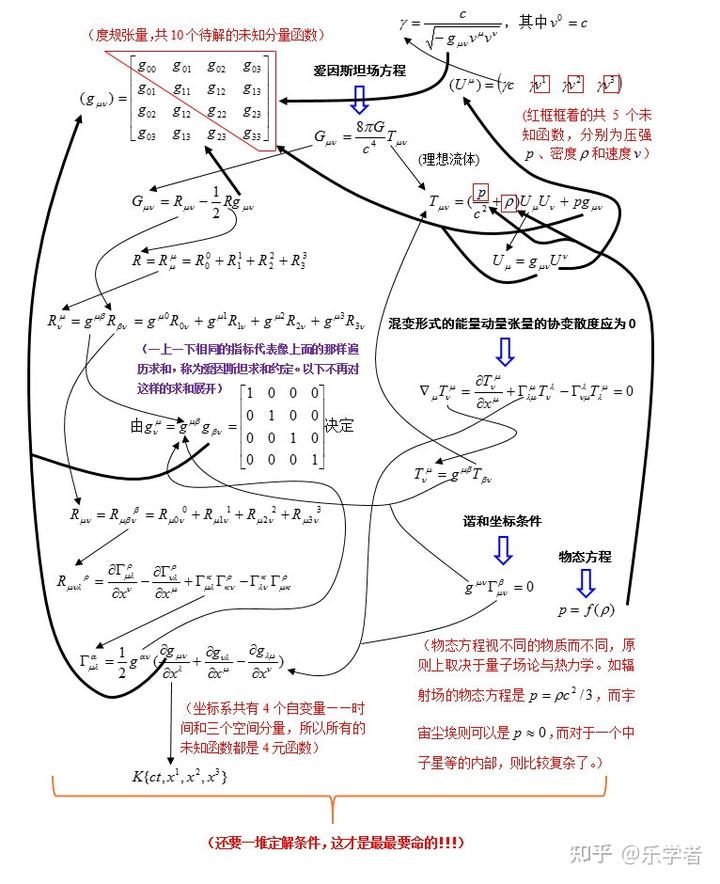
可见爱因斯坦场方程有多复杂。而上面的公式全是缩写形式，如果把这些缩写全展开的话，这个场方程到底会有多复杂，大家可以从下面的结果感受一下。下面仅仅是一个相对简单点的能量动量张量的一个协变散度为 0 即

$T_{0;\mu}^{\mu}=0$

的展开式，就有 76 页之多，这还是理想流体。没错，是 76 页！因为我们要求的是（清晰的脉络见上面的图）：

$(U^\mu)=(\gamma c,\gamma v^1,\gamma v^2,\gamma v^3)$

其中

$( v^1,v^2, v^3)$

是要求解的三个未知函数，且有

$\gamma =\frac{c}{\sqrt{-g_{\mu \nu }v^{\mu }v^{\nu }}}$

，

$v^0=c$

。按上面的全景图，它的展开顺序是首先给出能量动量张量

$T^{\mu\nu}$

的混变形式：

$T_{\text{ }\nu }^{\mu }=\left(\rho +\frac{p}{c}\right)U^{\mu }U^{\beta }g_{\beta \nu }+p \delta _{\text{ }\nu }^{\mu }$

然后计算其协变散度：

$T_{0;\mu}^{\mu}=\frac{\partial T_{\text{ }0}^{\mu }}{\partial x^{\mu }}+\Gamma _{\lambda \mu }^{\mu }T_{0 }^{\lambda }-\Gamma _{0 \mu }^{\lambda }T_{\lambda }^{\mu }$

而其中克氏符的计算表达式是：

$\Gamma _{\mu \nu }^{\rho }=\frac{1}{2}g^{\rho \beta }\left(\frac{\partial g_{\mu \beta }}{\partial x^{\nu }}+\frac{\partial g_{\beta \nu }}{\partial x^{\mu }}-\frac{\partial g_{\mu \nu }}{\partial x^{\beta }}\right)$

而克氏符中的

$(g^{\rho\beta})$

还不直接是要求的未知度规，

$(g_{\mu \nu })$

才是，而用

$(g_{\mu \nu })$

表示的

$(g^{\rho\beta})$

就很复杂，它是：

就这么一步一步的算下去，把

$T_{0;\mu}^{\mu}=0$

展开成用待求解的未知函数及其导数来表示，最后导出成 pdf 文档就已经是有 76 页 pdf 文档的体量了。如下：

（这前面省去了 75 页...........................，下面只贴出最后一页，没错，是 76 页)

76 页！！这还只是 15 条方程中的一条，还有 14 条呢。而且这 76 页算什么呀，再算一下爱因斯坦张量

$G_{00}$

展开吧，有多少页呢？大家可以猜，其实我没有算之前也不知道有多少页，但算出来之后大吃一惊，居然有 1850 多页，这使得我把它转换成 pdf 输出时不得不分成两个文件，第一个文件 750 多页（只贴头尾）：

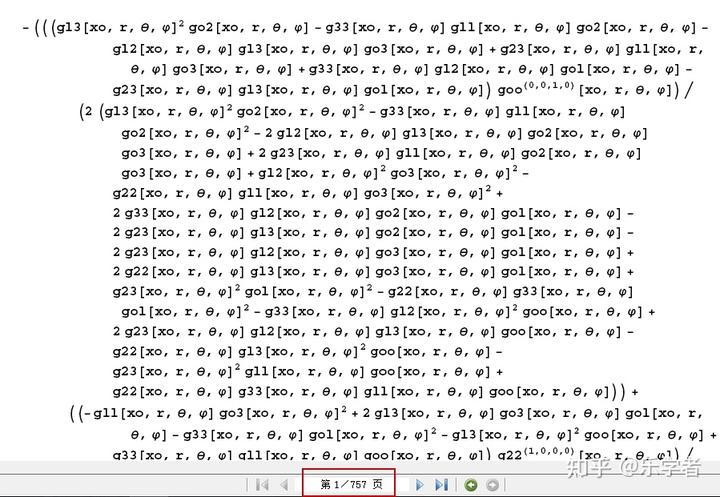
（这里省去了 755 页............)

第二个文件有 1112 页，下面的第一页是紧接着前面的第 757 页的：

（这里省去了 1100 多页............)

下面我们看到它妥妥的是二阶的偏微分方程：

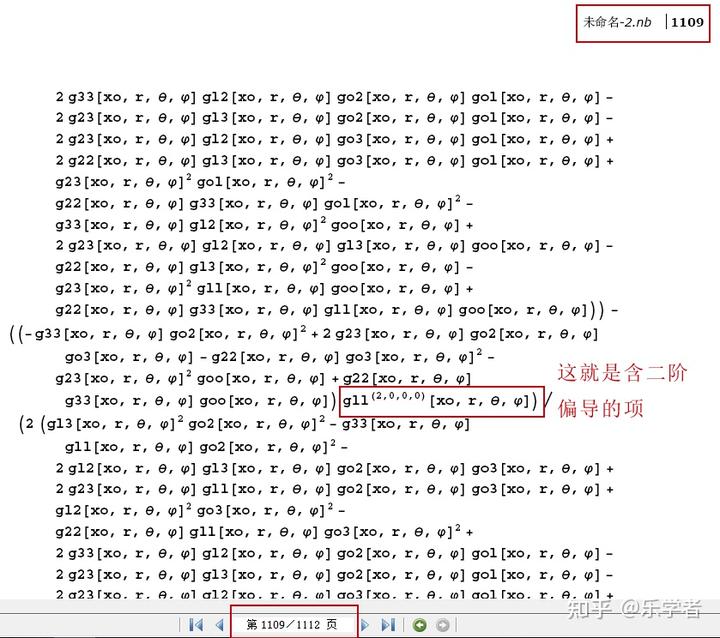
这么复杂的方程——共有 15 条同等甚至还要复杂的方程呀！不敢相信呀！我们再一步一步的看这么复杂的

$G_{00}$

是怎样炼成的。下面我们从度规开始，一步一步的给出这个方程的各个部件的展开式。首先是

$(g^{\mu\nu})$

的展开式，这前面已经贴出过了，大家可以看前面的，这已经相当复杂了。下面我们来看“第一层零件”克氏符

$\Gamma^\beta_{\mu\nu}$

的一个分量

$\Gamma^0_{00}$

的展开式：

注意！上面仅是克氏符的一个分量，而克氏符可写成 4 个

$4\times4$

的矩阵，由于对称性每个矩阵和度规一样有 10 个像上面那么复杂的独立分量，所以像上面这么复杂的独立分量就一共有 40 个。可见单是组成场方程的零件克氏符就已经够复杂了。

接下来我们来看“第二层零件”曲率张量

$R_{\mu\nu\lambda}^{\text{ }\text{ }\text{ }\text{ } \text{ } \beta}$

的一个分量

$R_{000}^{\text{ }\text{ }\text{ }\text{ } 1}$

的展开式：

（这里省去了 33 页............)

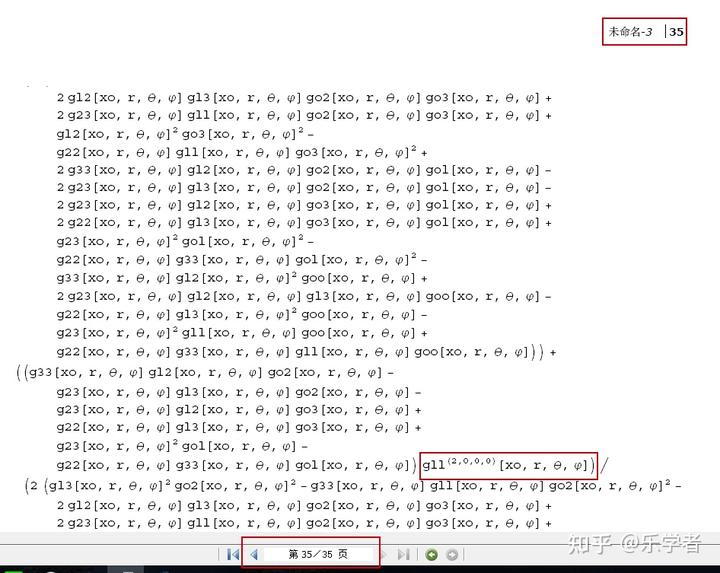
看到了吧，共有 35 页。而就算省去对称的分量，曲率张量是有 20 个独立的分量，即共有 20 个这么复杂的表达式。所以，进一步运算出的

$G_{00}$

有 1800 多页 pdf 文档也就不奇怪了。当然，这是完全的展开，考虑到有一些项可以化简，那么就算

$G_{00}$

化简后可以“减肥一半”，那也有 900 页呀。而由于我的计算机只是个人电脑，要把这么复杂的表达式化简，不知要算多少天了。所以

$G_{00}$

化简后可以“减肥”多少，我也不知道。

而这上面的仅仅只是基本的方程，还有定解条件呢，这是二阶偏微分非线性方程，每个 4 元二阶的未知待解函数要有 8 个边界条件（阶数乘以自变量的个数，有 4 个自变量），待解的度规分量就是 4 元二阶的，10 个未知度规分量将需要高达 80 条边界与初值条件。来台超级计算机并专门编写优化的程序吧，普通人是玩不起这东西的。这就是——广义相对论场方程从尝试求解到放弃。当然，真正求解场方程时，可不是这么暴力的玩的，科学家们研究爱因斯坦场方程的解法已经有 100 多年了，对于怎样用计算机求解这个场方程（如计算两个黑洞的合并等）已经发展成了一门学科——《数值相对论》）：

全书正文共有 400 多页。为解一个方程而发展出一门学科，其教材有 400 多页厚，这个方程有多复杂可想而知。这本书说是《数值相对论》，但全书你不会看到一条程序代码，既没有 c++ 语言，更不会有 java、python 或 Mathematica 。全书只有公式，除了公式之外还是公式，眼花缭乱的公式！

当然，世事是没有绝对的，对于简单的情形（如球对称），我们还是可以对它求数值解的。例如：

可以通过求爱因斯场方程的数值解来求太阳内部的压强吗？

广义相对论场方程看上去很简洁，但是实际上这个方程到底有多复杂？

相关推荐