软件画图有时候会把图像画“崩”掉,常见于隐函数图像,以及图像中含有间断点的情况。比如之前画过的一个“破丝袜曲线”:
请问这个方程图像有什么性质?
画崩了的原因之一是程序只能用有限的精度表示浮点数。在此限制下有一些本不该得到 0 的算成了 0,或者应该相等的地方判定成了不相等之类,画出来的图像就变得破碎。
如果发生破碎的地方本身也是有规律的,它与原始的图像亦或是其他的破碎之处甚至可能发生“干涉”产生复杂的花样:


有一些软件可以提高画图的准确性,比如 Mathematica 里指定
PlotPoints→50
,大幅提升画图效果,仅有少量的崩坏点残留:

对付隐函数的神器 GrafEq 能得到非常准确漂亮的图像,代价是画图耗时比较长:
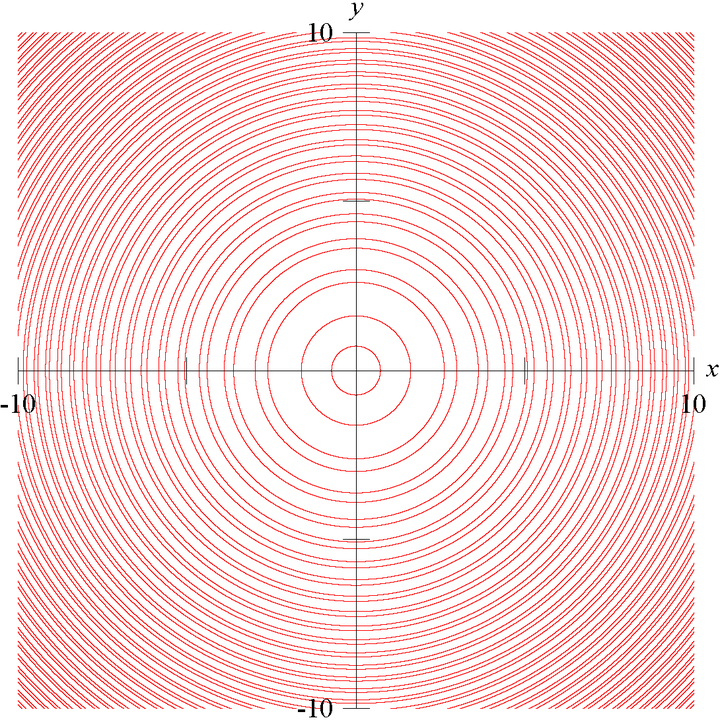
对于本提问给出的具体方程,手动分析一下画图的过程也不错。以最里面的 6 个圆为例——
令括号里的东西
,满足方程的
就是使
的那些值:
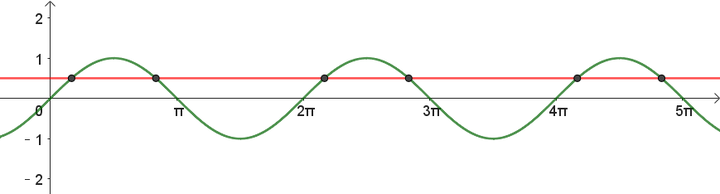
目前这些点的横坐标是
,但是
却是半径为
的圆。那么我们可以把这些
往函数
上面映射一下,把它们变成
:
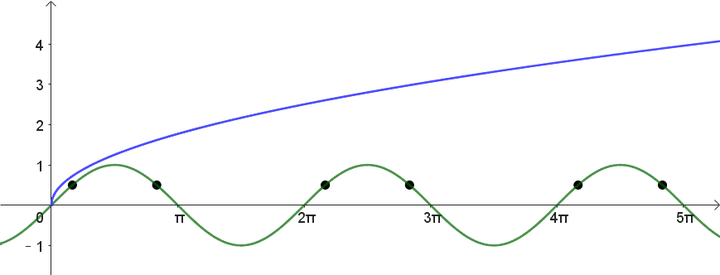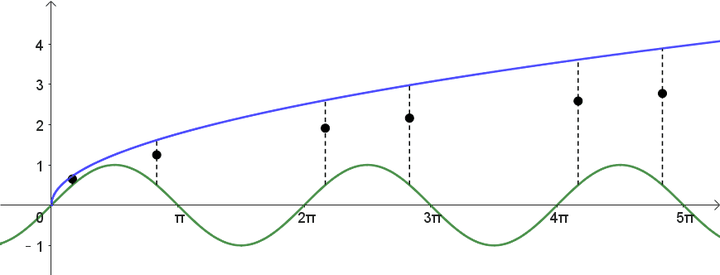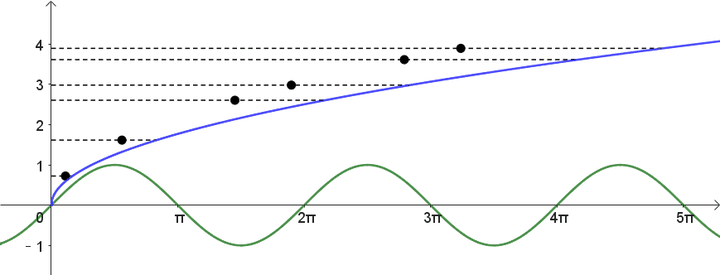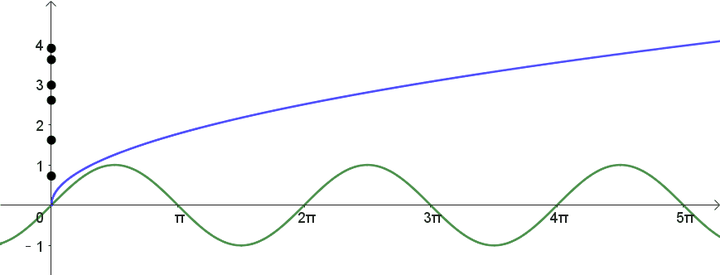
现在这些
都在 y 轴上,不必担心,因为画圆的时候只会用到它们与原点之间的距离。将这些点绕着原点画圆,就是原始方程的图像了:
像这样找到每个圆的半径,并在软件里画这些圆(而不是直接画原始的方程),一点也不丑陋了对吧:
(直接画圆都会崩的话这软件可以狗带了)

可以看到图像是两个一组、从中心向外间隔越来越近的同心圆。
「间隔越来越近」源于上面拆分画图步骤的第二步
是一个斜率越来越小的映射。换用别的映射就能得到不同方式分布的同心圆。
比如最简单的
,这是
的图像:

再如
,应该是间隔越来越远的同心圆对吧(由于
增长得太过迅速,给它添加一个系数 0.0001)。

这对应的是
的图像。
要是直接画它的话,只能说是非常抽象了:



 微信扫一扫
微信扫一扫 



