微分:是当自变量x 变化了一点点(dx)而导致了函数(f(x))变化了多少。
比如,国民收入 Y=f(c),c 是消费,那 c 变化了 dc 时,会导致 Y 变化多少呢?变化 dY,这就是微分,而 dY/dc 就是这个单变量函数的导数。把微分 dY 视为 dx 的线性函数,那么导数就是这个线性函数的系数:注意,这个视角甚至可以推广到微分流形、泛函,等你以后深入学习到更高的层次就会知道,现代数学对于微分的认识是:算子“d”代表着从流形上的 n-1- 形式场到 n- 形式场的一种线性映射。这里作个解释:流形,你就理解为弯曲 / 扭曲空间,二维流形直观上你可以理解为曲面,但还是有区别,因为我们说曲面总是想着三维空间中的一张曲面,也就是说,我们默认是把曲面嵌入到三维欧式空间中去的,但流形意味着我们把曲面本身当作空间去研究。流形理论里的“微分”有很多很多:我们说的算子 d 叫外微分,除此之外还有协变微分 / 协变导数,李导数,等等。这里就不扯那么远了。
差分:粗糙地讲,就是离散化的微分,即
y。当变化量很微小时,就近似看成 dy。差分的概念还是比较初等的,高中就应该接触不少了。
变分:无限维空间上的微分,我们一般称之为Frechet 微分,其实就是微分在无限维空间的推广(照搬)。Frechet 微分作用于泛函就叫变分。这里就不扯什么泛函分析里的 Banach 空间微分理论了,简单说下,泛函是将函数空间(无限维空间)映射到数域,就是,把一个函数映射成一个数。打个比方,从 A 点到 B 点有无数条路径,每一条路径都是一个函数吧?这无数条路径,每一条函数(路径)的长度都是一个数,对吧?那你从这无数个路径当中选一个路径最短或者最长的,这就是求泛函的极值问题。有一种老的叫法,函数空间的自变量我们称为宗量(自变函数),当宗量变化了一点点而导致了泛函值变化了多少,这其实就是变分。变分,就是微分在函数空间的拓展,其精神内涵是一致的。求解泛函变分的方法主要有古典变分法、动态规划和最优控制
————————————————————————————————————————
时隔很久,回知乎看了一下,楼下有关“变分”的回答是错误的,居然还有很多人回复说“豁然开朗”。都给我看下图:
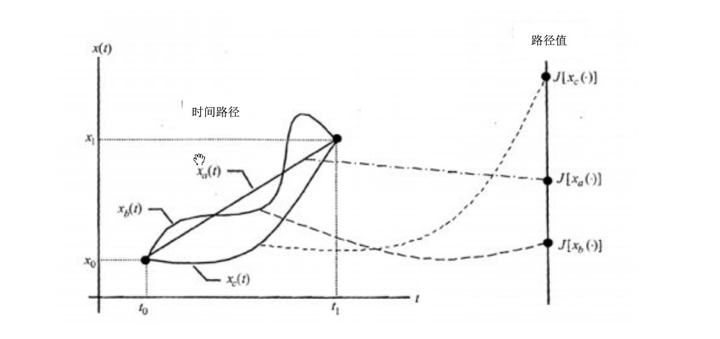
坐标轴里三条黑线叫做函数,这个都知道,函数是把 n 维空间的一个点映射成一个数!
图片里虚线对应的映射是泛函!看清楚了,泛函的取值取决于系统的整体路径,泛函将整条路径映射成一个数!也就是说,原来的函数 X(t)成为了泛函的宗量 X(自变函数),t 从此以后退化为参数!不能再叫泛函的自变量了!泛函的自变量是函数整体!函数整体!是整个路径的变化!楼下说“变分是函数关系发生微小变化而自变量不变时引起因变量的变化”这个理解是错的,因为这个时候自变量已经退化为参数了,它变不变无所谓!
我建议数学功底好的同学亲自去看看《非线性泛函分析》的书,数学实在不行的同学,仔细看看有关变分法或最优控制理论的书籍!建议在校同学有条件的最好自己多去图书馆看看,尽量少花时间在网络上问问题。

 微信扫一扫
微信扫一扫 



