这里分成两个问题来回答:第一,为什么地球自转我们会感觉不到?第二,对于我们感觉不到的东西,为什么愿意相信?
第一,为什么地球自转我们会感觉不到?
因为没有参照物。在时速 300 公里的高铁上(封闭外视车窗)我们感觉不到高铁在前进,在时速 700 公里的飞机上,我们也同样感觉不到速度。如果我们把地球看作是宇宙间的“高铁”,假设在它运行的轨道旁有快速移动的景色,我们就很能容易感觉到地球的运动。可近处没有这样的东西。
我们也没有办法在空间中打上一根钉子作为绝对参照物。因此,只能依靠较远的、看起来似乎是静止的天体作为参照物。事实上,那些天体也绝不是“空间中的钉子”,只不过因为它们实在太遥远了,所以我们不妨——事实上恐怕也是唯一的选择—这些遥远的恒星作为参照物。所以,一个物体不受外力作用的时候,将一直保持它的运动状态。这也是牛顿第一定律的内容。[1]
人感受不到地球的转动,还有一个原因是相对于地球的体积来说,地球转得太慢了,角速度太低。自转一圈需要一天的时间,公转一圈更是需要一年。宇宙中有些中子星一秒钟能自转好几百圈,如果地球的自转角速度增大到一定程度,人就能感受到地球的自转。
我们根据向心力的公式计算一下:
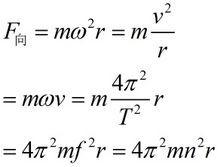
假设一个质量 60kg 的人站在赤道上,赤道的半径大约 6379km,赤道上的线速度大约是 466m/s,代入向心力的公式 mv/r 可得人需要的向心力大约是 2N,这仅仅是人所受重力的 300 分之一多一点点,所以人感受不到地球的自转。至于地球的公转,影响就更小了[2]。[3]
如果地球自转的角速度逐渐增大,人需要的向心力就会跟着增大,增大到一定程度就能可能被人感受到。比如,自转角速度变为现在的 17 倍,赤道附近的物体受到的万有引力,就会提供物体随地球自转需要的向心力,物体就能飘起来。如果角速度再大一点,赤道上的物体就被地球甩到太空。[4][5]
其实我们用心观察,还是能体会到地球自转带来的影响。北半球上的河岸右侧被冲刷的要比左侧严重一些,这就是地球自转带来的效应。
1851 年法国物理学家傅科为证明地球自转,他设计出一种摆,后来被称为“傅科摆”。
傅科摆绳长 67 米,绳端摆锤重 27 千克,这种摆自由摆动时间较长,便于人们观察。摆下有一个有刻度的圆盘,盘上刻有通过圆心的直线。静止时,摆锤正中应对准盘的圆,观察时先确定盘中某一直线与通过圆心的子午线重合,然后推动摆锤沿。

为了观察到方向的改变,实验地点需要设置在顶棚很高的厅堂中,顶棚用来悬挂钟摆。傅科最后选择了巴黎高耸的国葬院作为实验场所,并在摆的下放安置了一个沙盘。在摆运动时,摆尖会在沙盘上划出一道道的痕迹,从而记录了摆动方向。实验的结果与傅科的设想完全吻合,摆的摆动显示为由东向西的、缓慢而持续的方向旋转。[6]

摆放置的位置不同,摆动情况也不同。在北半球时,摆动平面顺时针转动;在南半球时,摆动平面逆时针转动。纬度越高,转动速度越快,在赤道上的摆几乎不转动,在两极极点旋转一周的周期则为一恒星日(23 小时 56 分 4 秒),简单计算中可视为 24 小时。
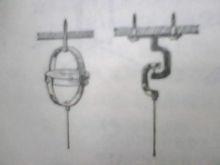
悬挂摆的支架一般却要带动它参与地球的自转。为解决这一问题,傅科采取了一种简单而巧妙的装置-万向节(如下图),从而使摆动平面超然于地球的自转。
傅科摆的摆动平面偏转的角度可用公式θ°=15°tsinφ来求,单位是度。式中φ代表当地地理纬度,t 为偏转所用的时间,用小时作单位,因为地球自转角速度 1 小时等于 15°,所以,为了换算,公式中乘以 15°。[7]
根据上面的计算结果,可以发现傅科摆在地球的不同地点旋转的速度是不同的,这也说明了地球表面不同地点的线速度不同。我们可以利用傅科摆在某一位置的旋转速度,通过相应的公式来确定这一位置所处的纬度。
那么,傅科摆为什么能够演示出地球自转呢?简单的说,因为惯性。按照牛顿第一定律,在一个固定的参考系中,一个物体不受外力作用的时候将一直保持原来的运动状态。正常情况下,给摆一个适当的初始作用,他就会沿着一个固定的方向运动。
再来看第二个问题,为什么会我们相信自己的经验感受不到的东西?
这个问题就涉及到人的科学信仰问题。科学,是千古以来人类理性自我肯定的结果,即,人是相信人自身的理性是可以通达无限的。而科学便是人类理性发展的产物。通常科学家会设计实验并控制各种变因来保证实验的准确性,以及解释理论的能力。
而一个来自卡尔·波普尔的观点认为,人类其实无法知道一门学问里的理论是否一定正确,若这门学问有部分有错误时,人们可以通过严谨明确的证明这部分的错误,的确是错的,那这门学问也算是合乎科学的学问。[8]
至少今天,我们生活在一个相信科学、信奉科学的世界中,对于一些不相信现有科学的人,最大的挑战是你需要想办法提供可以让科学家们打脸的证据。科学的实验的确可会有错误,现在科学家的科学理论在未来的某个时刻也可能会被推翻,但是,在没有找到一个好的证据去证明他是错的时候,任何人都没有理由去反对它。

 微信扫一扫
微信扫一扫 



