这是一个非常好的问题。在这个问题背后,蕴含的是最近这一百多年来物理学中好几个学科的发展:电动力学、原子物理、固体物理、量子力学。要回答这个问题,我们首先澄清“透明”的概念。
1. 日常生活中的“透明”
在日常生活中,当我们能看到某物体背后的情况时,我们就说这个物体是“透明”的。我们可以看到玻璃外面的景色,对于金属则只能看到表面的光泽。从这种角度来说,“玻璃是透明的,金属不是”。


2. 物理意义上的“透明”
在物理学中,物体的“透明”程度是用“透过率”来描述的,就是说有百分之多少的光能透过物体。透过率越大,我们就更加容易看到,物体越透明;透过率越小,物体就越不透明。当然,这里是用人眼作为参照,你要是搞一个单光子探测器去接收透过物体的极弱光信号,那我只能说你作弊了。
许多答主已经提到,“透过率”实际上是与波长密切相关的。在人眼可视的光波段,(大部分)金属的透过率约为 0/(普通)玻璃的透过率大于 90%,即“金属不透明”/“玻璃透明”。但当波长慢慢变短或金属厚度变薄时,金属的透过率并不为 0,这时金属又变成“透明”的了。然而,这已经超出普通大众接触的范围了,所以咱日常生活中也没看到这样的现象(然而用紫外激光器做过实验的各位铁汁:说到这儿我可就不困了啊【更正:其实日常生活中也有,见本文第 3 小节结尾处】),也就理所当然地认为玻璃透明,金属不透明。
既然要对物体透不透明的本质追根溯源,那接下来我们就一步一步地、从宏观到微观地说明“透明(不透明)“的物理含义。越往下,涉及到的物理知识越多,供不同水平的读者阅读。这里先给个文章观点的总览。
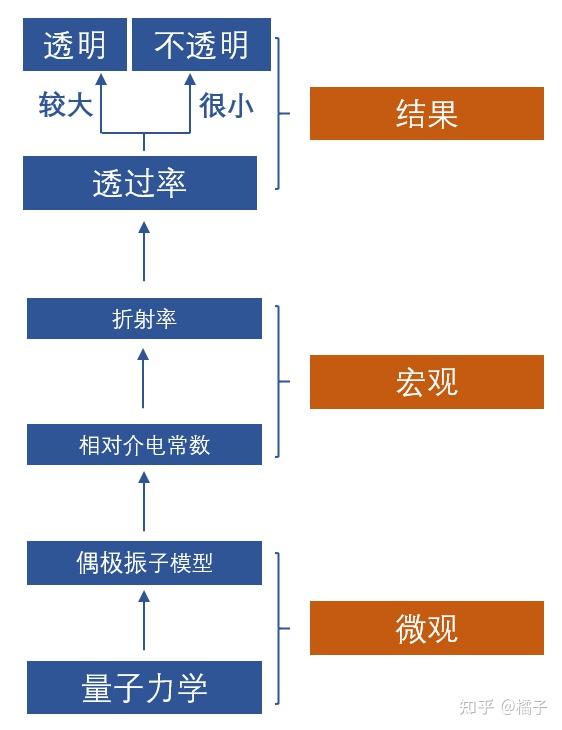
迫切需要答案的,请移步第 6 小节。但是我强烈建议有基础的铁汁能按步骤阅读(或者至少先看完第 3 小节)。
以下描述中,为了通俗易懂会牺牲一部分严谨性,请专业读者仔细甄别。
3. ”透明“与物体的折射率[1](Level:高中 / 大学)
不过在聊”透明“和透过率的关系之前,我们先说说反射。因为如果打到物体上的光大多被反射回去的话,动动脚趾也知道透过率会很低。在大多数情况下,只要存在两种材料的分界面就一定会有反射。反射的多少和界面两侧的材料折射率有关。
折射率是大家很早就接触过的物理名词。“真空中光速与物体中光速的比值为该物体的折射率”,那时我们知道光在空气中传得快,水里传得慢。正因为不同材料中光的传播速度不同,我们才能推导出熟悉的折射定律。那为啥在介质中传得慢呢?这篇回答越往后会给出答案。这里我们先认为折射率是物体的一个固有属性。
先看下面这张图的正入射简单情况,光从上方(折射率
,空气)射入,进入下方(折射率
,金)时会在界面处产生反射。
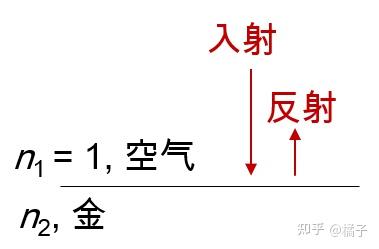
具体反射多少呢?反射率
可以由下面的菲涅尔公式算出来:
有了这个式子,下面就以
是金作为例子做一些小小的计算。
或许有人想问,你咔咔就整个公式,这个式子怎么来的?要得到上面这个式子,你首先得知道电磁场的边值关系。那电磁场的边界条件又是咋来的呢?答案是麦克斯韦方程组,人类最伟大的方程之一。这里就不把推导放出来了,因为会劝退很多人(因为我懒)。
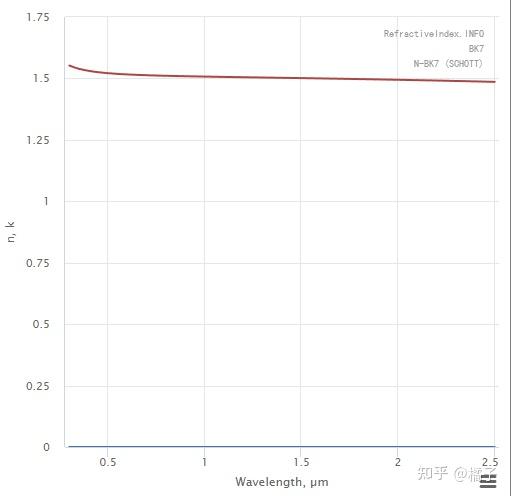
这张图画出了金的折射率
与波长的关系。
为啥折射率一直在变啊?高中可没说折射率是变化的嗷。emmm,我现在只能说这是材料的色散。详细的解答放在后面。
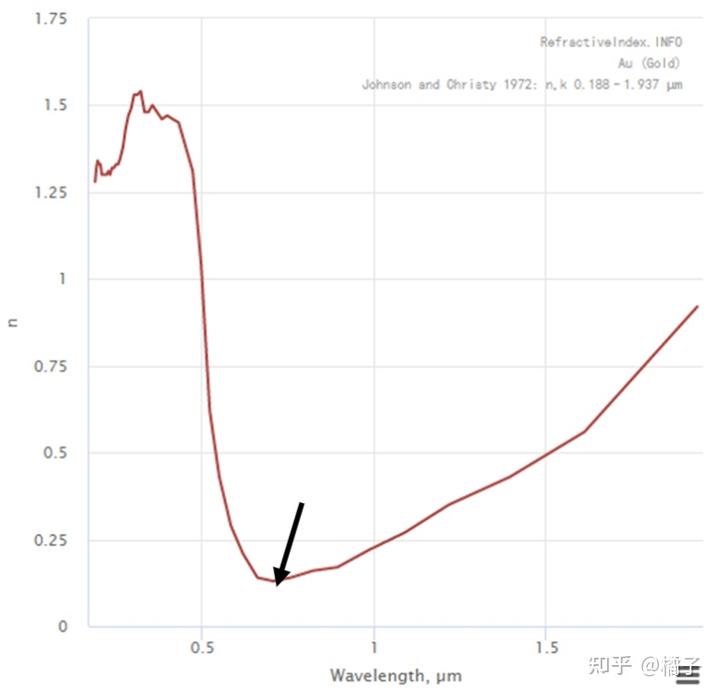
让我们先把目光往图中箭头部分集中一下。在 705 nm 这个波长,金的折射率
,此时
,说明金在这个波长是高反射率材料。实际上,在 550-800 nm 波段内,金的反射率都很高(大于 80%),这也说明了金为什么会显示出”金黄色“。这一点也可以这样理解:由于这个范围内金的折射率小于空气,那么金相对空气来说属于光疏介质,因此从空气射入(光密到光疏)时很容易发生全反射,因而对外呈金色。
But,我们还没解释金为啥不透明呢。那就看看透过率
呗。还是 705 nm 这个波长,经过计算,透过率
。这点透过率,那还能看得到个啥呀。
等等,或许有人已经黑人问号脸了?刚才 705 nm 这个波长算出来的反射率不是 0.97 嘛,咋透过率只有 0.00002 了?还有,我把
代到反射率公式里算出来的
不是 0.97 啊?我知道你很急,但是你先别急。
问题出在哪呢?问题出就出在金的折射率不是实数,而是包含实部和虚部的复数。下图画出了金的折射率实部(
,红线)和虚部(
,蓝线)随波长的变化关系。

为什么要引入折射率虚部
呢?因为实际情况下,部分材料会对外界光有吸收。对金属,则更是如此。所以用虚部
来表示材料的吸收,因此也称
为消光系数。705 nm 波长下,金的复折射率是
。现在把折射率带入反射率公式就能算出正确的
啦。那为啥透过率只有 0.00002 呢?刚才说部分材料会有吸收导致光被消耗,出来的光就更少了,与之相关的物理量是吸收系数
。
吸收系数与折射率虚部的关系是:。
的量纲是
,也就是每单位长度上的衰减。比尔定律告诉我们:光在材料内部是按
指数的方式衰减的。
也就是说,光经过金内部时会逐渐被吸收,导致最后的透过率比(1- 反射率)更小。看下面这张图。
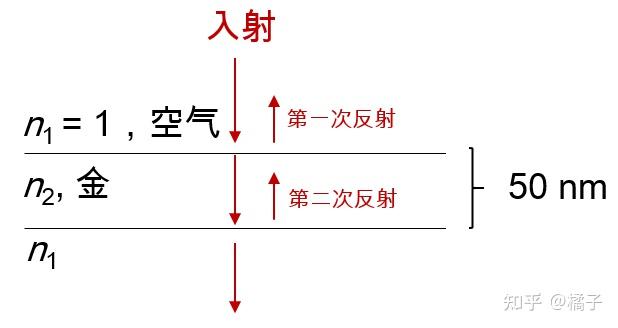
光在穿过金膜(假设 50 nm 厚)会经历:两次反射 + 金膜厚度的指数衰减,所以实际的透过率是
。把吸收常数
,金膜厚度
代进去就能得到 0.00002 的透过率啦。【大多数情况下】我们接触的金都是体材料,那透过率就更低了,自然是不透明。
上面的计算中忽略了金膜内部的多次反射。在材料厚度很薄时,还要考虑多次反射 / 透射造成的干涉效应。展开的话就是薄膜光学的研究内容了,咱就 8 聊了。
这也能解释题主的疑惑:为什么光在不同的材料中穿透程度不一样?因为材料的吸收系数不一样。并且,吸收系数也和光的波长(频率)相关,所以不同波长的光在相同的材料中穿透程度也不一样。
为啥玻璃透明?因为它对光的吸收太弱(折射率虚部很小)啦!假设玻璃折射率是 1.5,那么空气 - 玻璃界面的反射率是 0.04,透过率大约是
。所以我们才能看到玻璃外的景色。
也有一些答主从玻璃是非晶体的角度去解释。日常生活中的玻璃的确是由多种材料制成的非晶材料。但主要成分还是二氧化硅,二氧化硅是晶体啊。它的光学性质完全可以由折射率来描述。即使是宏观上的玻璃,也能用折射率去概括它的光学特性。你甚至可以去测玻璃的折射率,向下面这样。我用量角器在屏幕上大概量了一下,入射角大约是 35 度,折射角大约是 20 度,那么根据折射定律可以算出玻璃折射率大约是 1.68,和上面假设的折射率 1.5 略微有些出入(考虑到测量误差和材料种类不同,这个值也能接受吧)。

对于普通大众,了解到“折射率影响透过率”这个程度基本上已经差不多了。但是,对于想刨根问底的物理爱好者,咱还得继续往下研究研究。
但是在这之前,我想先对日常生活中玻璃的一些透光现象作简单地解释。因为这些情况暂时还用不到更深的物理。
- 为啥整块的玻璃是透明的,有裂纹的玻璃就有点看不清了呢?

这是因为在裂纹处产生了很多不平整的空气 - 玻璃界面,来自玻璃后方的光入射时,会产生各个方向的反射和透射。透射光和反射光可能再次碰上不规则的界面,又产生各个方向的反射和透射。这个过程可能发生多次,导致真正反映玻璃后方情况的光没法直直地进入眼睛,而可能向四面八方散去,导致人眼感官上难以看清。裂纹越多,就越难看清。表面粗糙的磨砂玻璃,透光却不透明的原理类似。
2. 为什么有些玻璃在透光的同时还有各种颜色?

这种玻璃只对特定波长光产生吸收,导致透过的光中缺少某个波长而产生颜色。当只透红光和只透绿光的玻璃叠在一起时,就只能看到一团漆黑,向上面那张图一样。此外还有其他类型的有色玻璃,可以参考这篇文章。
3. 单边透视(仅有一侧透明的玻璃)的原理是啥?

这玩意儿经常用在汽车后座车窗玻璃、嫌犯审讯室等场合。它的原理是在玻璃一侧镀上一层薄金属膜。这层金属膜呢,既可以透一部分光,也能反一部分光。通过控制膜层的厚度,可以使反射的光比透射的光更多(一般反射是透射 2 倍),来达到单边透视的效果。为了实现最好的单边透视效果,环境内外的亮度差越大越好。所以电影里,审嫌犯的屋子都开着亮灯,高级警察或证人都站在玻璃暗侧暗中观察。
4. ”透明“与物体的相对介电常数(Level:大学)
上面都是用折射率来描述物体整体上、宏观上的光学性质。接下来,我们稍微深入一点,看看折射率与材料的什么特性有关。
首先,折射率在高中课本里定义为
(
为真空中光速),它反映的是光在介质 / 物体中传播速度变慢的程度。折射率越大,光传播得越慢。
接下来我们稍微调转一下目光,回到麦克斯韦方程组(怎么老是你?)。由麦克斯韦方程组可以推导出电磁波的波动方程(懒癌发作,咱就 8 推了),从波动方程中可以得到介质中电磁波的传播速度
为
其中光速
。发现了没,这不就是说
嘛。这里我们先姑且讨论
的情况,那么就更简单了,
。也就是说,折射率实际上就是相对介电常数开个根号。
有人想问为什么只讨论的情况?因为足够简单。而且在题主问题的讨论范围内,这种情况都是合理的。
但是相对介电常数的物理意义是什么呢?聊光在介质中的传播为什么要扯到这玩意儿呢?因为聊光的传播就不得不聊光的电场分量,如何解出介质中的电场,就要和相对介电常数打交道。
这里先给个印象:它反映的是介质在外场作用下的电场响应(极化、反抗)程度。接下来带大家回顾一下电动力学(苏醒吧,猎杀时刻到~),想不起来也没关系,有个印象就行。
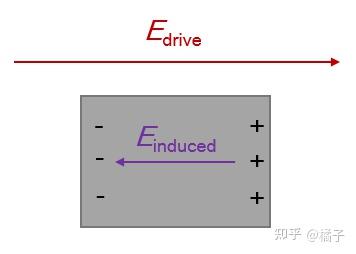
如上图所示,介质在外场
(比如入射光的电场分量)作用下,原子或分子的正 / 负电中心不再重合,被拉开后介质内部的微小体积出现束缚电荷分布(这种错位也产生了电偶极矩)。这些束缚电荷分布将等效地产生一个抵抗外场的极化场
。因此介质内部的电场是外场和极化场的叠加。怎么算出叠加之后的场呢?答案是高斯定理(麦克斯韦方程组中的其中一个)。这里不放公式真滴 8 行了(因为这一小节是”大学“水平,所以偷偷放个高斯定理应该妹毛病吧)。
注意哈,方程右边的电荷密度
既包含自由电荷密度也包括束缚电荷密度。这个式子的物理意义就是:电场
的源是总电荷分布,即刚才讲的外场和极化场叠加的结果。现在我们需要把束缚电荷密度的贡献从方程右边剥离出来,毕竟自由电荷密度才是更加容易控制和观测的。
为了把束缚电荷密度的贡献从右边剥离出来,我们把它放在了左边,并用
来代替束缚电荷密度的这部分作用。这里引入了一个新的物理量
:电极化强度矢量,与介质内部正负电中心错开产生的电偶极矩有关。我知道你们现在很晕,但是你们先别晕。可以这样理解:束缚电荷分布正是宏观电偶极矩产生的源嘛。
一般情况下,电极化强度
和
存在线性关系,即
,
为介质的极化率(暂时先不管它的物理意义)。佛了,怎么这么多符号啊!兄弟萌,这暂时的复杂都是为了最后的简单!此时散度算符括号里的那坨就可以写成
终于,相对介电常数
出现了!它数值上等于
,物理上反映了介质在外场作用下的电场响应(极化、反抗)程度。上式中的
称为电位移矢量,是一个辅助物理量,有了它,我们可以得到更简洁的高斯定理
那么测得了
,就可以算出
,然后再根据材料的介电常数算出
。
也许有人已经看出来了,介质的极化模型好像很眼熟——往两块平行电容板中间插入相对介电常数为
的介质,电容会发生什么变化?
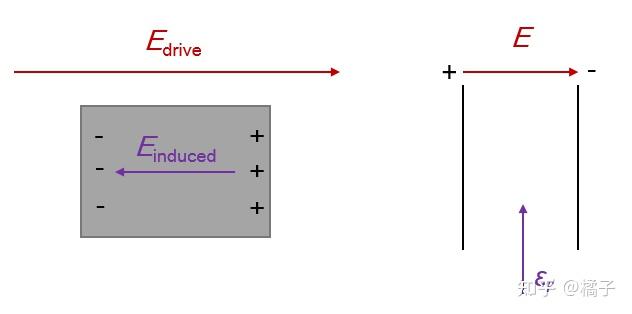
在没有上边一串知识的加成下,我们也能定性地作以下分析:介质插入后,介质的极化场将会抵消一部分原来的电场,导致电容板间的压降降低。在充电量为定值的情况下,这意味着电容将会变大。现在,我们要站在更高的位置去看问题了:插入介质后,相对介电常数由 1 变成了
,电容又与
正相关,当然是变大了。所以,你能看到在某些教材中也有把
称为相对电容率的说法。
扯远了,让我们回到答主的问题。
注意,相对介电常数仍然是从宏观角度去描述物体的光学性质(比如透不透明)。那相对介电常数究竟是咋来的呢?为了说明这个问题,我们需要往微观的角度继续深入。
5. ”透明“与偶极振子模型(Level:大学 / 研究生)
在经典电动力学中,处理光在介质中的传播问题通常分成两步。第 1 步,把光纯纯地视作电磁波,什么光子、量子别来沾边;第 2 步,把介质中原子 / 分子的行为视为偶极振子。
最经典的振子模型就是弹簧。小球带动弹簧偏离平衡位置时,会受到一个恢复力的作用。这个力将导致小球趋于回到平衡位置。在回到平衡位置的过程中,小球会获得速度导致再次偏离平衡位置。这个过程如此往复,形成振荡。振荡的频率与弹簧弹性系数
正相关,和小球质量
负相关。用数学公式描述这个过程其实就是一个简谐波。
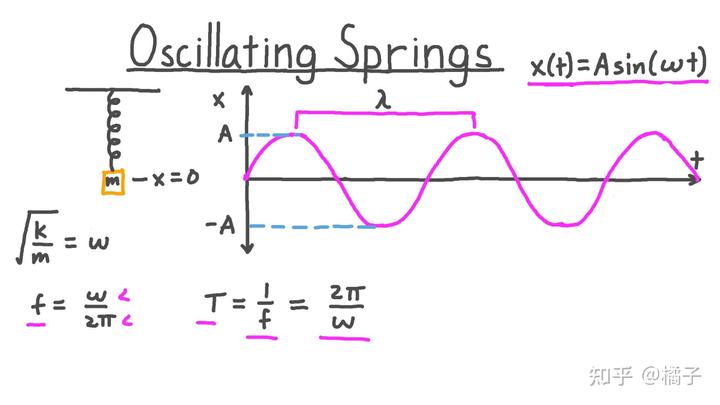
谐振子模型在动力学里是如此的经典,导致物理学家 Lorentz 在处理光传播问题时也借鉴了这套振子理论。其实那个时候 Lorentz 根本不清楚原子是啥、电子是啥、振子物理根源是啥。你会发现科学家的连蒙带猜和我们凡人差距是真的大。
OK,让我们康康微观偶极振子模型。在绝缘体和半导体中,最重要的是束缚电子的振荡行为;而在金属和掺杂半导体中,最重要的是自由电子的振荡行为。这里,我们暂时把这些笼统地称为“电子”。
”我早就想问了,啥是束缚电子,啥是自由电子啊?”要解释它需要一些原子物理、固体物理的知识。别急,我们在后面会给出解释的。
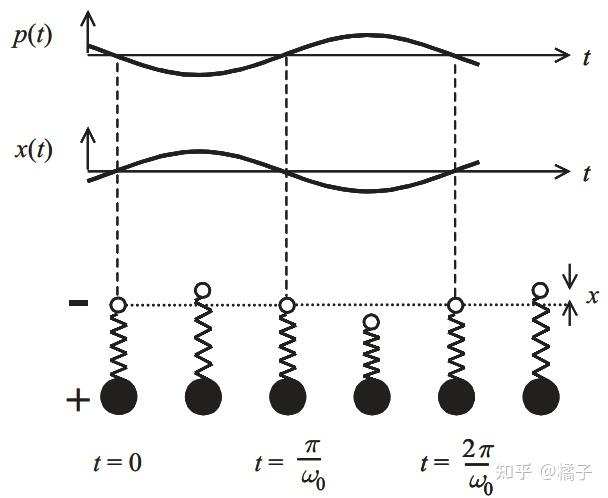
在上图所示的电子振荡模型[2]中,黑色实心圆圈代表原子核,空心圆圈代表核外束缚电子。电子与原子核之间的作用用”弹簧“来等效(弹性系数
,关于它的物理意义后面再介绍),参考弹簧振子,偶极振子的固有振荡频率为
其中
为电子质量。因此类比一下弹簧振子,偶极振子模型就是说:电子在平衡位置附近来回振荡
,形成时谐变化的电偶极子
,然后向外辐射电磁波。
可以预见,当携带频率
的外界光场与原子相互作用时,存在共振和非共振两种情形。发生共振时有
,原子的振动振幅达到最大,即能量从电磁波往原子发生转移,也就是说原子吸收了入射光场能量。注意,这里的吸收和第 3 小节讲的由折射率虚部导致的光吸收不是一回事。
从量子的观点可以作如下解释:当入射光子的能量刚好为原子基态和激发态之间的能量差
时,原子吸收光子的能量从基态跃迁到激发态。但是,原子并不是一直稳定在激发态,而会通过非辐射跃迁或辐射跃迁的形式回到基态。前者最终将以热能的形式耗散,后者则会再次往外辐射光子,形成在介质内部传播的光场。参考第 6 小节。
好了,背景先介绍到这里,接下来我们回到相对介电常数。在第 5 小节说过,相对介电常数
与介质中诱导产生的电偶极矩有关,电偶极矩则与电子在平衡位置附近的相对位移有关。为了算出
,我们首先要算出电子偏离平衡位置的位移
(假设原子核不动,因为相比电子它太重了)。为了算出位移
,要先写出它的动力学方程。首先分析下受力,电子振荡受阻尼力、恢复力、外电场力的作用,然后把这些力全部写到微分方程里面去,像下面这样
上式中等号左边第二项描述的是阻尼力(
阻尼系数),第三项是恢复力,等号右边是外电场力。咔咔求解这个微分方程,得到
有了
,那每个电子引起的电偶极矩是
;假设电子的密度是
,那么介质内总的电极化强度矢量就是
在第 5 小节,我们有提到过
,
这两个式子,和上面一对照就会发现
即相对介电常数与频率(波长)有关,该现象称之为介质的色散(这便解释了第 3 小节中材料的折射率为什么随波长变化)。那么介质极化率
(表达式中 1 后面那坨)的物理意义也就清楚了,它反映了介质中宏观电偶极矩产生的容易程度,与外电磁场频率、介质本身特性有关。
最关键的,相对介电常数是一个复数!因而折射率是一个复数!正是虚数部分对应了光的吸收,或者更准确地说,光的"消耗"!
如果单独把相对介电常数的虚部画出来,它的两个特点是:
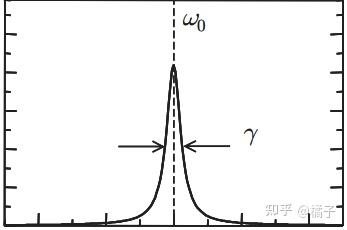
1)当
时,虚部达到最大。很好理解,能量匹配之后被吸收了嘛。
2)虚部在频率域上的谱宽和
有关(数学上可以推导)。
我们仔细看看相对介电常数的表达式,发现虚部正是含
的那一项引起的。
代表啥?是振子受到的阻尼力啊。阻尼的物理起源是啥?先卖个关子。
实际情况中,偶极振子的固有振动频率并不只有一个。
回忆这个式子。不同的振荡频率,说明有不同的
或者
。前者代表原子核对电子的束缚程度,越内层的电子栓得越紧,
越大,
越大,产生偶极共振就需要更高的频率,这与“光子能量越高越能激发内层电子”的结论相符,所以有些材料在可见光波段以下由吸收峰;后者代表振子的有效质量,当需要考虑:1)原子核和电子的共同振荡;2)极化分子的振荡时,振子有效质量
变大,意味着
变小,对应所需的共振频率也变低,所以有些材料在红外波段也有吸收峰。
那么对应每个振动频率附近,都会有一个吸收峰,类似下面这样。在每个吸收峰中间,介质都可以认为是透明的(因为吸收很小)!
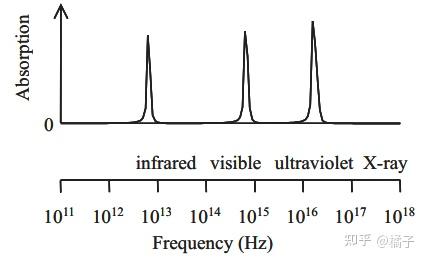
对于玻璃,它在红外波段有两个吸收峰(21 um,9.1 um),在紫外波段(150 nm)也有一个吸收峰。在这些波长下玻璃有较强的吸收,它会不透明。但是这些波长已经远离日常生活,所以不太直观。
需要说明,上面说的偶极振荡模型存在很大一个缺陷:它预测的吸收峰在每个频率
的强度都是一样的。但看看上面这张图,每个吸收峰的强度其实是不一样的。为了修正模型,只好被迫在分子上加入一个振荡强度因子
来描述实验现象。然而,实际上这个
在经典电动力学中找不到对应的解释,后面会看到只有量子力学才能合理解释。
仔细阅读的铁汁会发现我一直在说“介质”这个词,它一般情况下都指绝缘体或半导体。如果是金属又会发生什么呢?
还记得之间说的束缚电子和自由电子吗?现在我们稍微区分一下。在绝缘体、半导体(没有掺杂的)中,电子被原子核栓得比较紧,这时称它们是“束缚电子”,因此会有一个固有振动频率
。在金属或掺杂半导体中,(外层)电子已经拴不住了,这时称它们是“自由电子”,它们在振动时不受原子核给的恢复力,
是 0。
比如金属钠,它的核外电子排布式是,处于
轨道上的那个电子就是自由的,原子核栓不住它。量子力学决定了电子栓不栓得住。
那么,金属的相对介电常数就可以写成
现在,先暂时忽略
这一项,然后考虑两种极限情况。
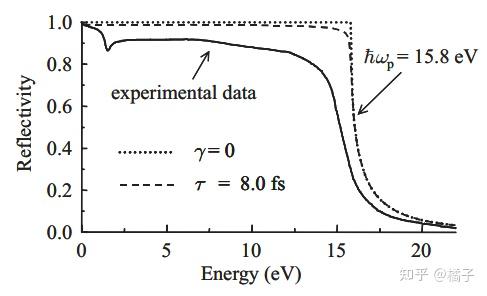
1) 频率非常高,金属的相对介电常数趋近于 1,根据反射率公式,金属此时不反射。
2) 频率非常低,金属的相对介电常数小于 0,根据反射率公式,金属此时高反。
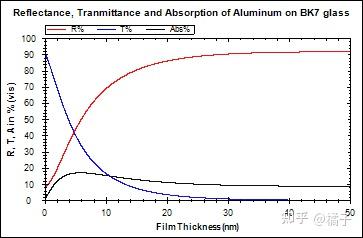
以上两点虽然是在近似条件下获得的,但是和实验结果仍然相当符合。比如下面展示的铝的实验结果。这也便说明了金属并不是一直都不透明。
6. ”透明“与量子力学(Level:高中 / 大学 / 研究生)
所谓遇事不决,量子力学。终于到了这一部分,我觉得恐怕也是许多知友最关心的部分。由于这部分过于玄学,我在这里做一些概括性的描述(没办法,摆公式就是装逼和原罪...当然,这部分包含一些个人理解,有误的地方请各位在评论区指出并理性讨论)。
一般大家都会从能带论的角度去解释光子是被电子吸收,或是不与电子发生作用而顺利通过材料。
从能带论发展来的半导体物理,是当今整个信息技术行业的基础。能带论告诉大家:绝缘体、半导体、金属是以带隙宽度来区分的。能带论的底层方程就是大名鼎鼎的薛定谔方程。
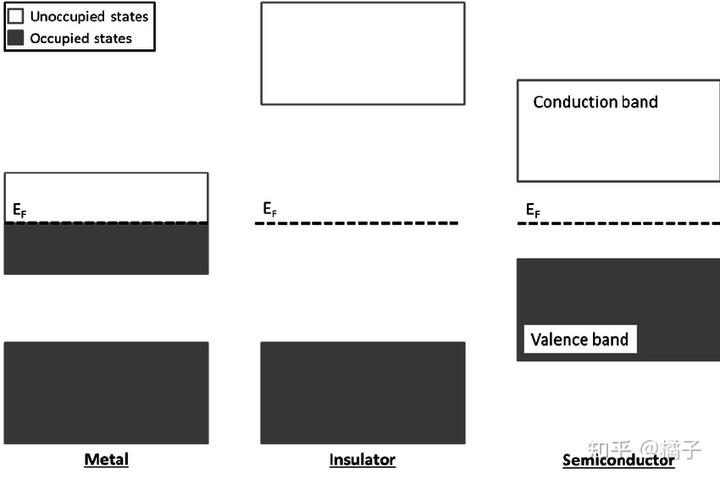
就是说光子携带的能量刚好弥补材料带隙宽度时,光子的能量被电子吸收(对应偶极振子模型中
);如果光子能量低于这个带隙宽度,光子就和没事人一样不和电子发生作用,顺利通过介质。而普通介质(比如玻璃主要成分二氧化硅)的带隙宽度很大,可见光能量比它低,所以可见光可以穿过介质。
还有一些答案是从光波长和原子密度 / 晶格尺寸的线度对比角度去写的,说是波长短(对应高频),小于原子间距轻松穿过;波长长(对应低频)与晶格发生碰撞过不去。这实际上 makes no sense。SiO2 的晶格常数在几个埃[3],可见光依然可以“穿过去”。
一些答案在这就浅尝辄止了。错了吗,也没错,但因为没有把整个物理过程全部说完,容易让人误以为光子能量让电子跃迁到激发态时就代表了光的消耗,导致材料不透明。
的确,电子确实会吸收光子能量往高能级(这里说能级其实是不严谨的,因为在晶体中原子能级已经劈裂形成能带,但是我这里还是用能级的说法方便大家理解)跃迁,但是电子并不是一直都呆在高能级上,它还会回去。最关键的是,它回到低能级的过程也会辐射出光子。这个过程才完整描述了光在材料中的传播。
1. 费米黄金准则(Fermi's golden rule)告诉我们电子跃迁是概率事件,它在频率的跃迁几率对应的就是偶极振子模型中的振荡强度因子
,参考第 5 小节。
2. 电子“回去”的过程需要时间,这个可以帮助大家理解为什么光在材料中的传播速度为什么会变慢。电子“回去”辐射光子的过程,在经典电动力学中的对应就是光场在材料中引起偶极振荡,振荡的偶极子再次往外辐射电磁波的过程,参考第 5 小节。
那到底什么过程才对应了真正意义上光的消耗呢?
那还是要看电子从激发态回到基态的这个过程。这个过程其实又可以分为两个子过程:非辐射衰退(non-radiative decay)、辐射衰退(radiative decay)。前者是说电子回去的时候不发出光子,通常这部分能量最终转化成热能,代表了光消耗的物理,构成宏观上光的吸收(即第 5 小节中偶极振子
项的物理来源);后者描述的才是电子“回去”发光的过程。但是呢,后者其实又和两个物理名词联系起来:自发辐射和受激辐射。自发辐射是说再发射(re-emit)的光子和吸收的光子在方向、相位上没有任何关系,完全随机。受激辐射是说 re-emit 的光子和吸收的光子可以视为“完全一样”。自发辐射和受激辐射一起,构成宏观上的反射、透射光。
那又有人问了,那玻璃在可见光波段的透反射是咋回事呢?这里带隙宽度大于可见光能量,总没有电子跃迁,没有辐射衰退吧?emmm,其实也不是没法解释。量子力学中,光子能量和电子跃迁不是 0,1 关系,而是概率关系:电子跃迁几率和光子频率通过费米黄金准则联系在一起。也就是说就算光子能量低于带隙宽度,也会有跃迁,只不过几率更小而已。此时,大部分电子都倾向于维持原来的状态,少部分以极低的概率跃迁,因此大部分的可见光发生透射,仅有少部分被反射。
当然,还有另外一种完全量子力学(totally quantum mechanically)的解释。咱不说光子、不说光波,咱只说概率,光在某个位置出现的概率。这些概率通过一系列量子力学式的复杂计算都能算出来,无论反射或透射。
To calculate this quantum effect requires you calculate every possible path along with the probability of the photon being on that path. It is quite complex, but the math works out[4].

 微信扫一扫
微信扫一扫 



