我来说一个非常常见的、但是没有学到物理专业高年级就不会懂的现象：磁铁。
其实，磁现象人们认识上千年了，但是直到一百年前我们才知道，它不但是一个相对论现象，而且也是一个量子现象。
知乎上有不少问题，问的就是“量子现象有没有宏观效应”云云。例如这个：
宏观上有量子效应吗？
对这类问题，大家很容易想到的是一些比较 fancy 的东西，比如说超导，超流动。但是大家并没有意识到，我们其实早在千年前就已经认识到一个纯粹的宏观量子现象了，那就是磁现象。
为何说磁铁只能用量子力学解释呢？早在经典电动力学的时期，不就有了安培的分子电流假说了吗？难道经典电动力学不早就预言了顺磁性抗磁性等特性吗？
答案可以引用费曼讲义中的一段话（第二卷 34 章）[1]：
Yes!—We are going to prove that if you follow the classical mechanics far enough, there are no such magnetic effects—they all cancel out. If you start a classical argument in a certain place and don’t go far enough, you can get any answer you want. But the only legitimate and correct proof shows that there is no magnetic effect whatever.
没错！我们要来证明，如果你严格按照经典力学的定律，将不会有任何的磁效应。如果你不太严格地遵循它，你的确可以得到你想要的答案。但是，真正合格且正确的证明将会告诉你，根本就没有磁现象。
我在这里可以用高中生的语言来谈一下，为何经典理论中不可能会出现宏观磁现象。
看完我的回答之后，你就会知道，高中课本（包括非物理专业的普物课本）里面教给你的东西，其实是错的。那么它为何还会教给你呢？因为它有用。
可以说，高中物理课本、大学的普物课本里面到处都是坑啊（我怀疑四大力学和高年级课本也是如此，只不过没有证据 ╮(╯_╰)╭）。
在这个过程中我们牺牲了理论的自洽性，不去讨论理论背后的那些纠结的矛盾，而只是给旧理论打上一个新补丁来用。如果你满足于实用，那么这样做的确没有什么问题。但是如果你对理论自身的问题还有好奇心，你就可以进一步发掘，去找到更深层的奥秘。
我们可以集中在一个问题上，来把这个矛盾暴露出来：
为何磁场不做功，但是磁铁却可以相互吸引 / 排斥？
磁场（严格说是静磁场）不做功，这一点在中学课本里是很清楚的了。因为洛伦兹力的公式是：
磁场的洛伦兹力总是和运动方向垂直。
而物质的磁性是怎么来的？初等课本里面是这样描述的，因为自旋或轨道旋转的原因，每个电子都是一个小磁矩。在磁场的作用下，这些小磁矩互相之间方向排列整齐，于是就产生了宏观的磁性。
从经典自旋来看，由于旋转产生的磁性，其在受力的时候，受到的仍然是洛伦兹力。也就是说，这个力不可能做功。那么，磁铁到底是怎么相互吸引的呢？
从经典电动力学中我们知道，一个磁矩在不均匀磁场中会受力（吸引或排斥）。我们因此可以建立一个经典模型：一个旋转的电荷（如下图）：
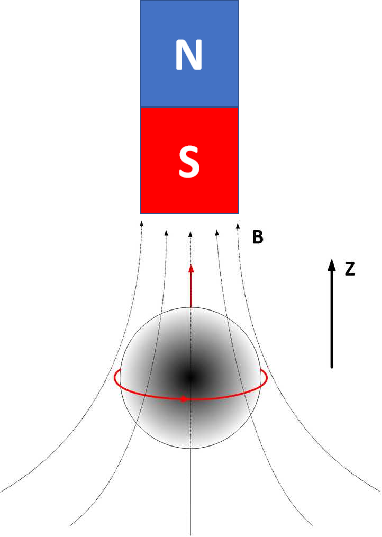
在这个图中，这个旋转电荷就是一个小磁铁。我们把它放置于 Z 方向的磁场中，磁场上部强下部弱。那么这个磁铁怎么受力呢？我们可以来分析一下它的受力。
首先，简化起见我们用一个带电的薄圆盘来代替这个小球。下图就显示了圆盘边缘的磁场方向。我们把磁场分解成两个分量：一个指向圆心
，另一个平行于 Z 轴
。
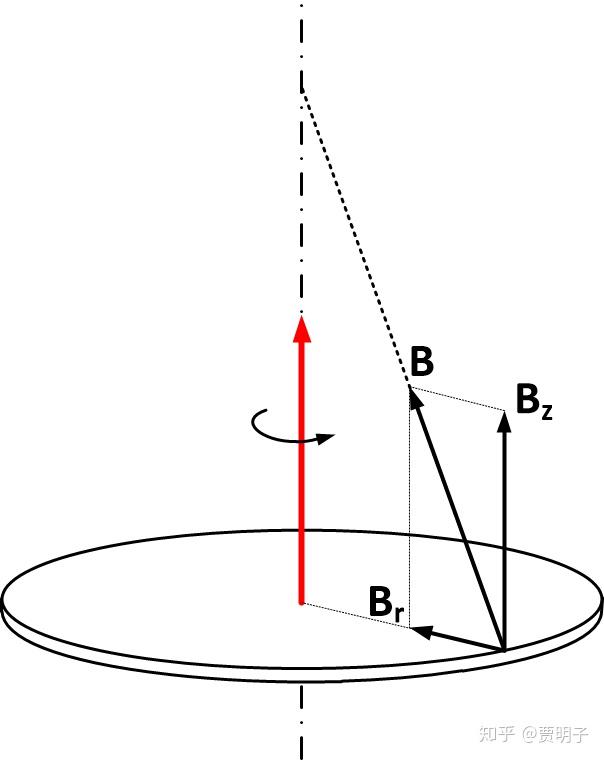
在圆盘的边缘，有一个切向的速度 v（如下图）。我们可以很容易得到，
因为这个速度所产生的的洛伦兹力是沿着径向指向外侧的。由于圆盘的对称性，这个受力就会被对面的受力抵消掉，因此它就没有任何的整体效果。
但是，
就不同了。它会产生向上的洛伦兹力（如下图）。圆盘处处受力都是如此。也就是说，整个圆盘就会受到向上的洛伦兹力。于是乎，圆盘就会向上移动。这就是宏观磁力的来源。
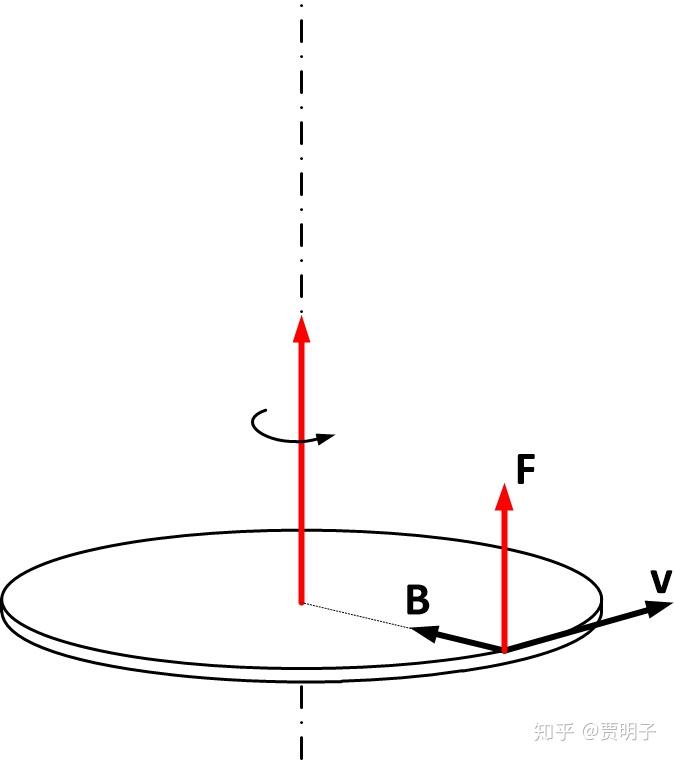
你可能说，这挺好的啊，这不是用经典电磁学解释了磁铁吸引的现象了吗？
但是故事还没完。且听我继续讲来。
当圆盘受到向上的作用力的时候，它就会向上加速移动。于是，整个圆盘就都附加上了一个向上的速度分量。而通过洛伦兹力的分析，我们很容易就得到，这个向上的速度分量就产生了一个切向的受力。而这个切向受力就产生一个力矩，这个力矩会抵消掉圆盘的旋转！（如下图）
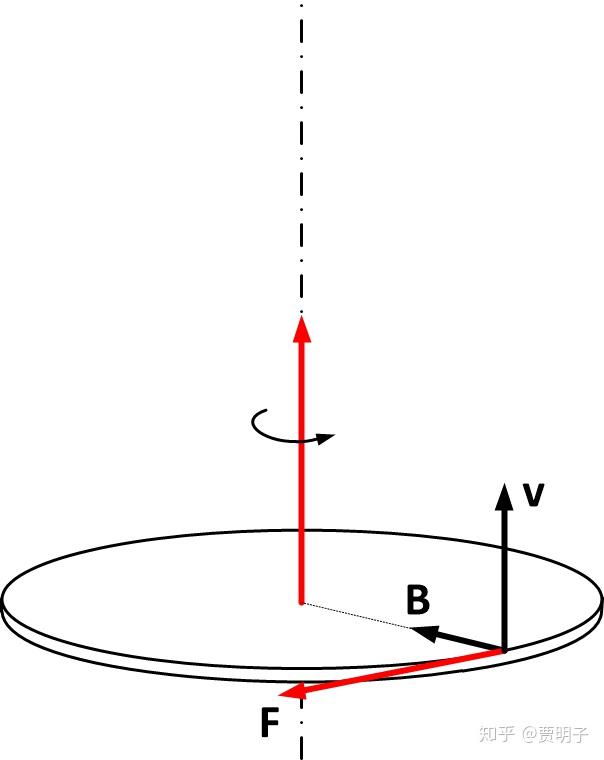
也就是说，从这个理论分析中我们会得到，当一个磁铁被吸引的时候，它自身的磁性会变弱，并且会持续变弱！
这显然和我们观察到的现象不符。
如果我们进一步仔细考虑这个过程，我们会发现，圆盘在受到磁力产生运动的时候，它的转动速度越来越慢的同时，它的平动速度越来越快。整个过程中的能量转换不外乎是转动动能和平动动能之间的转换，和磁场没有毛关系。
如果我们进一步，用一个圆环来代替圆盘。我们把初始旋转的带电圆环置于磁铁下方。我们会发现，圆环受到磁铁的吸引靠近，靠近的过程中，转速越来越慢，但是靠近的平动速度却越来越快。当圆环穿过磁铁中心的时候，它的转速变为零，但是此时平动速度达到最大。随着它因为惯性继续向上移动，它开始继续旋转，于是乎转动越来越快，平动越来越慢，就形成了一个震荡过程：
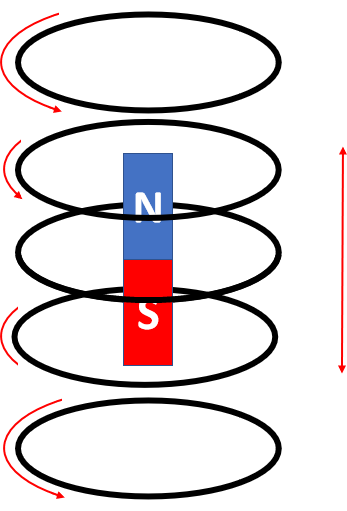
总而言之，没错，经典理论通过经典的旋转电荷的确可以解释磁铁在磁场中受力的问题，但是同时它会预言，磁铁在受力的同时，伴随着磁性的消失！这个可就不对了。
我们还可以用另外一个问题来阐述经典理论的无效。我们来看看磁化的过程。课本中描述的磁化，是物质中作为磁矩的电子在外磁场作用下排列起来。
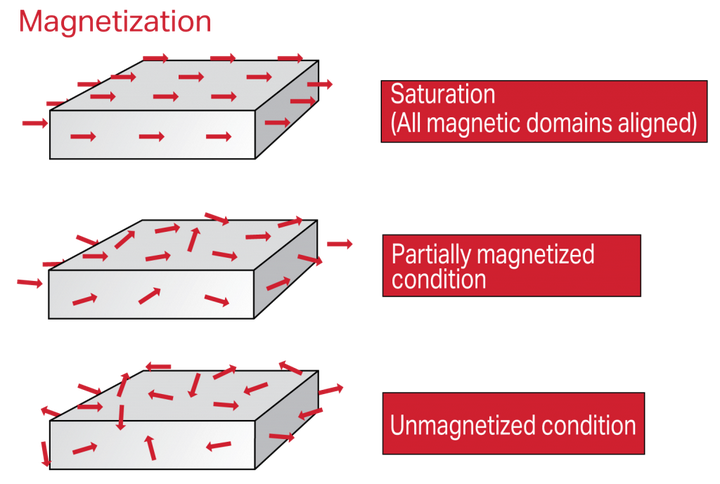
可是实际上，如果我们严格用理论分析一下就发现不那么简单。比如说我们仍然用一个转动带电圆环来作为模型。我们把这个圆环放置于一个偏斜的外磁场中，这个磁场可以被分解成两个分量，
和
：
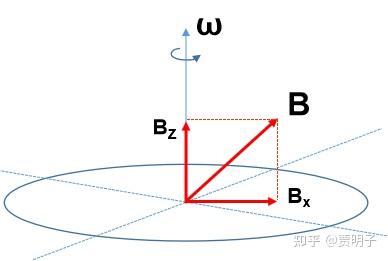
那么我们同样分析一下洛伦兹力对它产生的效果。我们来看
分量（如下图）。这个分量可以进一步分解成一个径向分量
和一个切向分量
。切向分量和速度一致因此不会产生效果，但是径向分量则会产生向上和向下的洛伦兹力。我们很清楚地看到，这个力的效果就会使这个圆环发生偏转，从而和外磁场一致起来。
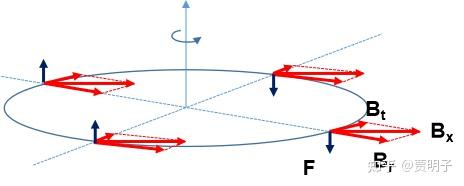
这的确解释了磁矩在外磁场作用下排列一致，但是同样地，这不是故事的全部。我们再继续分析一下。当圆环发生偏转的同时，它就有了附加的一个速度分量。而这个速度分量下，磁场就产生了额外的一个洛伦兹力。这个力的效果就是一个额外的扭矩，抵消掉圆环的旋转（为了保持高中的语言，我们这里忽略拉莫尔进动）。
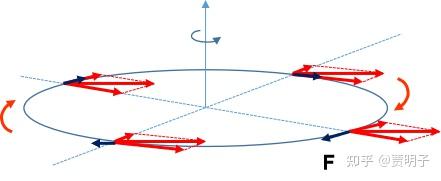
也就是说，它的确偏转了，但是代价就是自身磁性的消失。等它偏转到与外磁场方向一致的时候，在外磁场的方向上的净磁矩并没有发生任何变化！
也就是说，外磁场根本就不可能使任何物质发生磁化。这显然也是不对的。
其实，这个过程，有一个现成的定理，叫做Bohr–Van Leeuwen 定理。[2]这个定理需要一些超出高中的知识，这里就不多说了，它是这样说的：
如果我们严格地遵守经典统计力学和经典电动力学，那么任何物质都不可能产生宏观的磁性。因此物质的磁性必须是一个纯粹的量子现象。
那么，磁现象到底和量子力学有何关系呢？留个扣子吧，如果感兴趣的人多，再来更新。建议大家看看堪称量子力学经典实验之一的 Stern–Gerlach 实验。
更新一（2022/4/7）：
评论区有人有所疑问，质疑磁力的大小能否使得前面的带电转动圆环所模拟的经典磁环保持震荡。这里给出说明。
首先可以证明整个过程中圆环动能是守恒的。我们考虑轴对称一维模型。在任一时刻，磁场可以分解成两个部分，
和
。其中 z 方向上的磁场
对整体运动没有影响，因为它对 z 向运动显然没有任何影响，而在径向上会互相抵消。我们只需要考虑
的影响。
对角速度而言：
对 z 向速度而言
我们可以运用链导法则：
很容易可以得到：
所以我们可以看到，这个经典磁环在磁场的作用下动能保持不变。也就是说自始至终磁场并不能改变磁环的能量。
我们可以来计算一下它在磁铁的吸引下的运动情况。我们用一个理想通电线圈（尺寸：线圈的半径为 1，长度为 8）来模拟磁铁的磁场。这里用数值模拟三个情况。
第一种情况：磁环起始以较小的转动动能，而没有平动动能的情况下运动。也就是说，在初始时刻，磁环的平动动能为零，并且转动动能较小。我们可以计算出磁环的转动速度和平动速度随时间的变化曲线：
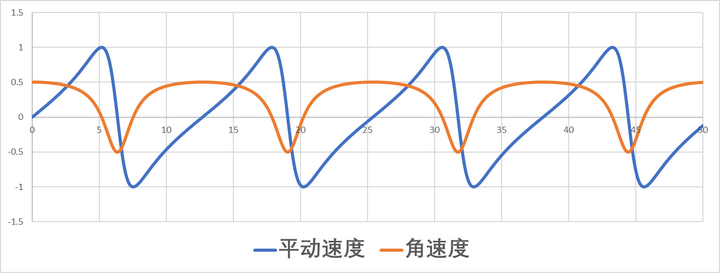
我用 python 写了一个小程序，来具体表现磁环的运动过程（磁环中添加三个“辐条”，用来表征转动。视频中的黑色方块就是磁铁的位置）：
https://www.zhihu.com/video/1495721146686935041
我们可以看到，此时磁环只是在磁铁下方震动，随着转动方向的逆转，导致它在 z 方向上受力不断发生反转，从而不断振动。
第二种情况：磁环在初始零平动，较大的转动速度开始运动。磁环的速度曲线和运动的视频就是这样的：
我们可以看到，在此时，磁环在磁铁的上下反复振动。
https://www.zhihu.com/video/1495721252292034560
微信扫一扫 
