方差单位和数据的单位不一致,没法使用。标准差和数据的单位一致,使用起来方便。具体说下吧。
1.标准差有啥卵用?
在描述统计学历四分位数(猴子:四分位数的位置计算原理?)的优点是可以从整体上描述出数据的分布状态,却无法告诉我们数据的波动性有多大。
我们举个具体的例子,在 NBA 中,平均数据用来衡量一个球员的战斗力,比如场均得分,盖帽,抢断,助攻等。
那么我们现在想一个问题。如果你是教练,你想知道哪位球员发挥最稳当。因为你需要一支值得信赖的球员队伍,他最不想要的就是表现时好时坏,水平反复无常,波动很大的队员。他需要得是分高,且发挥稳定的球员。
而标准差就是为了描述数据集的波动大小而发明的。
2. 什么是数据的波动大小?
很多统计概率的书本上会用离散程度和变异大小来表示数据集之间偏离平均值的程度。我一度被离散程度这四个字搞的摸不着头脑,因为大脑里根部无法直观的理解这四个字。想不通为何统计学家起名字的时候就不能通俗易懂嘛。
直到有一天,我想到“波动大小”可以直观的替代“离散程度”这个专业术语,我的内心是一阵狂喜。想想,我们日常生活中对一件事情的波动大小是有直观的理解的。
如果你像巴菲特一样在做价值投资,面对两支股票历年股价的曲线图,你可以直观的感受到哪只股票的波动比较大。
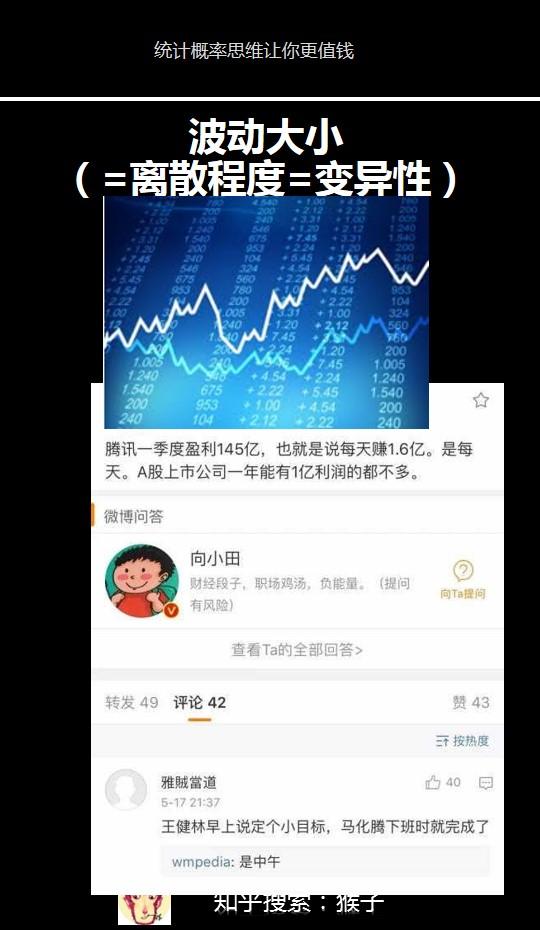
在例如你日常看新闻,会看懂腾讯 2017 年一季度盈利 145 亿,比去年同期增长
57%,也就是每天赚 1.6 亿,你会惊叹腾讯股价的波动性好大。想想王健林早上说定个小目标,马化腾下班时就完成了。
所以,以后遇到“离散程度”,“变异性”这些词理解不了的时候,你的大脑自动切换到“波动大小”这四个字,就理解了,因为他们说的是一个意思。
3. 标准差表示数据集的波动大小,那如何计算标准差呢?
直接上图吧(我喜欢画图,能用图说明的就不用文字)。

解释下上面的图,假设数据集中有三个数,分别是 x1,x2,x3。
第 1 步,先计算方差,每个数值减去平均数μ(miu),的平方,相加,然后除以数据集总数 n,这里有 3 个数,所以 n=3。
这样就算出了各个数值与平均值的平均距离。
第 2 步,方差开方就是标准差,标准差符号读西格玛。
别担心,当数据集中的数据很多时,会有专门的工具来计算出标准差。这里介绍公式是让你知道标准差是怎么计算出来的,对于后面的应用和理解会很有帮助。
4. 回到你的问题,为啥有了标准差,还要方差?
如果你理解了上面的公式,就会自动最终我们想要的是标准差,方差只不过是计算的中间过程。
你都衡量数据了,肯定要和你衡量的数据单位一致,不然比较个啥,标准差单位才是和数据一致。

5. 标准差应用案例
没有使用案例,懂的太多知识用不上就是耍流氓,下面案例不详细说了,来图吧。


 微信扫一扫
微信扫一扫 



