在这里,我可能要反对一下@赵泠了。
第一、“按照 2023 年的时间计算,它已经有 46 亿岁”这个理解是对的,但有一点小问题。
第二、地质学里面的年,也压根不是什么儒略年,而是回归年,所以“它已经绕了太阳 46 亿圈”对了一半。
一、为什么说“它已经有 46 亿岁”这个理解是对的?
因为目前的地球年龄的测定是依据放射性同位素测年测出来的,这是地球的绝对年龄。
我们都知道,很多元素并不稳定,它们会自发衰变,在衰变过程中释放电离辐射(α射线、β射线、γ射线等),变成一种新的较为稳定的元素(或是原本元素的同位素),这些元素就叫做放射性元素。我们直接能通过一种叫做“云室”的设备看到这些放射性元素的衰变过程。
在同种放射性元素衰变的过程中,它们的衰变常数λ都是固定的,说衰变常数可能有点专业,但它实际上与半衰期有一个对应关系:
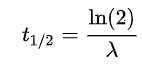
半衰期这个词很好理解,假设某一种放射性元素,其原本的数量为 1,当它衰减到 1/2 时,所经历的时间就是半衰期。对同一种元素来说,其半衰期是固定的,也就是说,它从 1 衰减到 1/2,再从 1/2 衰减到 1/4,再从 1/4 衰减到 1/8,这三个半衰期所经历的时间都是固定的。那么就可以通过计算这种元素从初始状态到现在经历过了几个半衰期(n),乘以它的半衰期(t),就能得到这种元素从初始状态到现在的时间长度。
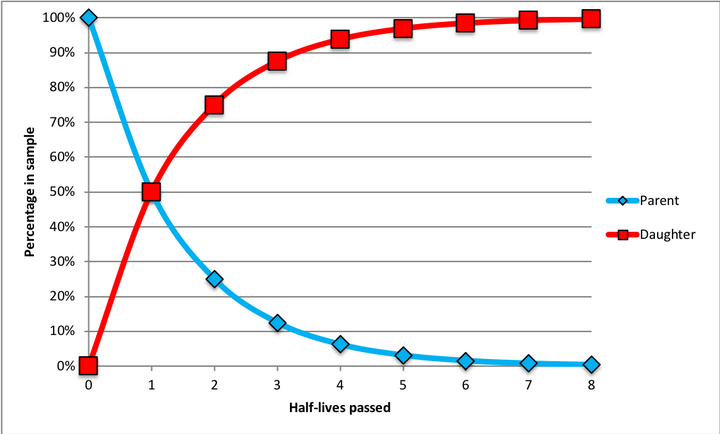
只不过,有些元素的半衰期非常短,仅有幺秒级(
s),比如氢 -5 的半衰期只有约 86 幺秒——与之对比,光行进 1 个质子直径的距离需要 6 幺秒;而有些元素的半衰期则非常长,比整个宇宙的年龄还要长万亿倍以上,比如碲 -128,其半衰期高达
s,比整个宇宙的年龄还长
倍。
但是好在还有很多放射性同位素的半衰期正好适合作为地球测年的标准,比如铀、铅、氩、钐等,其中最常用的就是铀和铅了——那么怎么使用呢?
以铀 -238 和铅 -206 为例,前者会自发衰变成后者,其半衰期为 44.7 亿年。我们假定在地球刚刚诞生的时候,其岩石中只含有铀 -238,不含有铅 -206,也就是二者的比例是 1:0。经过 44.7 亿年后,铀 -238 会只有原本的一半,剩下的都衰变成铅 -206 了,这时候二者的比例是 0.5:0.5。要是再经过 44.7 亿年,二者的比例是 0.25:0.75。
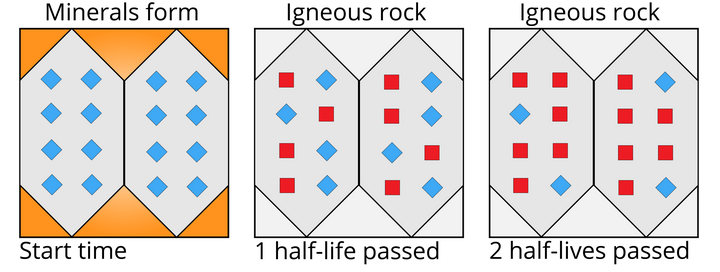
这种计算就是一个很简单的一次元方程问题,计算二者的比例,然后看看这个比例对应的半衰期数,再乘以半衰期(44.7 亿年)即可。
目前我们也确实就是按照这个逻辑计算的,只要找到一块岩石,计算其中的铀铅比例,就能算出这个岩石的年龄。
然后就会遇到一个关键问题:我们如何确定地球诞生时候的铀 - 铅比例?这一点在最后面我进行了补充在此不详细讲述。总而言之,我们最后得到的结果是距现在 45.4±0.5 亿年。
但是这个现在的定义并不是 2023 年,而是 1950 年[1-2]。
所以我说这个理解大体是对的,但有一点小问题,问题在具体年份上(也就是不是 2023,是 1950 或 2000)。
第二、为什么不是儒略年?
实际上一直到现在,地质学家们内部对于这个年的定义都有争议,虽然 2011 年国际纯化学和应用化学联合会(IUPAC)、国际地质科学联合会(IUGS)对地质学中的年做了定义[2],但很多人不同意[2]。
在这一版的定义中,IUPAC-IUGS 说的很清楚,在以往,地质学家们一直对地质学中的“年”没有清晰的定义,为了与国际单位制(SI)接轨,所以需要有这么一个基于国际单位制中的时间单位——秒(S)——的年的定义。
它们考察过多个不同的“年”,其中包括儒略年(Julian)、玛雅年(Mayan)、格里高利年(Gregorian)、回归年(Tropical)和恒星年(Sidereal),但是没有一个“年”的定义是满足要求的,因为地质年代的时间过于漫长,动辄百万起步,所以对“年”这个概念的要求是稳定、变化小。也就是说,在尽量长的时间内一年的天数和月数与地球绕太阳转动的周期是适应的,那么这就淘汰了基于地球自转制定的日历时间,因为误差很大,而只有基于行星围绕太阳公转的观测取得的结果才是更精确的。在这个基础上,IUPAC-IUGS选择了回归年,因为回归年每 100 年的误差只有 0.53s,并且具体定义一年的时间是31556925.445S。[2]
(PS,要是按照儒略历的算法,一年的时间为 365.25
86400=31557600S)

而回归年的定义就是:回归年(tropical year),也称为太阳年(solar year),是由地球上观察,太阳平黄经变化 360°,即太阳再回到黄道(在天球 上太阳行进的轨道)上相同的点所经历的时间。 相对于分点和至点,精确的时间取决于你在黄道上所选择的点[4]。
从这个意义上看,回归年确实就是地球围绕太阳转一圈,只不过这个转一圈被限定为 2000 年的转一圈。所以前半句话也有一半对。
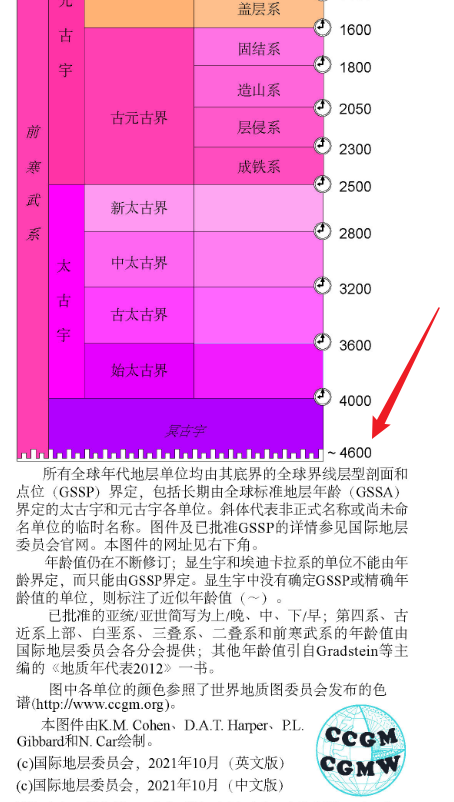
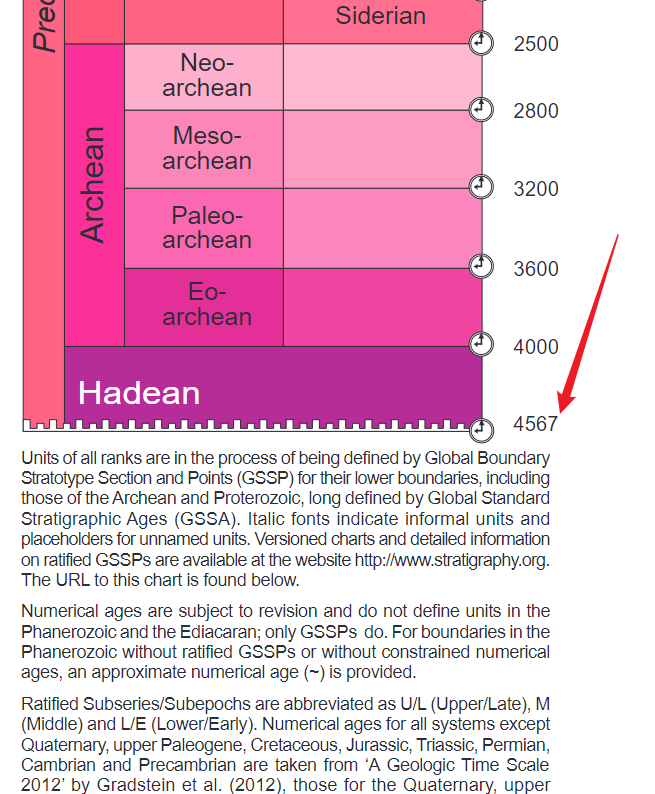
最后,地球年龄的问题,2021 版的国际年代地层表中,都还是约等于 46 亿年的,虽然 2022 年的改成了 45.67 亿年,但说 46 亿年也没什么大毛病。
放射性测年法补充
很多人对放射性同位素测年的方法很好奇,我在此稍微解释一下。
我在上文中写到的铀 - 铅同位素测年法是一个最基础的理论,也就是我们是如何利用放射性元素的半衰期测年的。
要具体使用这个测年法,首先需要了解在地球诞生之时的铅含量——这个含量是通过对铁陨石的测量得出来的,因为铁陨石不含铀,而它在现在的太阳系形成理论中,又几乎是与地球同时诞生的,所以铁陨石中的铅含量可以看作是地球上的初始铅含量,其中由于铅也有同位素(铅 -204、铅 -206、铅 -207、铅 -208),所以科学家们计算出来的实际上是铅同位素含量的比值,在 1962 年测出的这个值为(现代又不断有更精确的数据,但这并不重要,大家知道原理就行):

然后,由于方铅矿等矿物,不含有铀元素,所以从方铅矿形成到现在,其内部的铅同位素不会发生变化,这些铅同位素是地球从诞生以来,一直由铀元素放射性衰变而产生的。所以,我们可以用方铅矿中的铅同位素比值作为这些它们形成时地球的年龄,然后应用如下公式就能求得方铅矿形成时地球的年龄。

然后,再加上方铅矿形成至今的年龄即可。
除了铁陨石之外,陨石中还存在球粒陨石等其他类别,也可以直接测量它们中的放射性同位素年龄,以此作为地球诞生至今的年龄。
另外,在铀 - 铅同位素测年法之外,其实还存在许多其他的放射性元素测年法,比如 Rb-Sr 法、K-Ar 法、Sm-Nd 法等等,对这些元素的测年原理也都类似,结果也都差不多。
参考文献
[1] Aubry M P, Van Couvering J A, Christie-Blick N, et al. Terminology of geological time: Establishment of a community standard[J]. 2009.
[2] Holden N E, Bonardi M L, De Bièvre P, et al. IUPAC-IUGS common definition and convention on the use of the year as a derived unit of time (IUPAC Recommendations 2011)[J]. Pure and Applied Chemistry, 2011, 83(5): 1159-1162.
[3] Christie-Blick N. Geological time conventions and symbols[J]. 2012.
[4] 回归年 - 维基百科,自由的百科全书 (wikipedia.org)
[5] 柴田贤。地球年龄的计算[J]。国外放射性地质,1974(02):27-43。

 微信扫一扫
微信扫一扫 



