这本质在于几何定理的“推理连续性”太弱,很间断。
一个几何问题,当条件确定且是完备之后,其结论是否成立就是确定的了。
但是人们要用已知的几何定理手段去从条件推导到结论,可能并不是畅通无阻的,需要添加“桥梁”,这就是辅助线的意义。
几何定理往往是如同“两直线平行,内错角相等”这种“找条件,得结论”的定理,要能够运用它,至少要有平行线,所以很多辅助线就是作平行线,就是这个道理。如果不添加辅助线的话,我们所能利用的几何定理手段将无法施展,从而无法推理前行。
而另一方面,如果采用解析几何的方式,即转化为代数问题来解决,往往就不需要辅助线了,因为代数定理的“推理连续性”比几何定理强太多,代数的化简和变形过程是“连续的”,而且是可以“凭空”构造的,而且很方便地转化为另外的问题来解决。
这个可以从立体几何的传统几何法和建系法看出区别。几何法求二面角之类的,基本上需要作出这个角,找到各种几何关系去解三角形;而建系只需要找点的坐标,然后找面的法向量,然后就可由向量夹角公式计算了,解析几何的方法中间就没有几何法那样的“思维鸿沟”,而是很顺理成章的逻辑推理和计算。
很惊讶这个问题会突然爆发这么高热度,对于“推理连续性”的问题也引发了一些争议,本人才疏学浅,也只是信口拈来,并未对所谓逻辑推理的“连续性”作很好的定义,不知是否有相关领域的专家能够给出专业的解释。
对于非解析几何和解析几何各自的特点,我想在这里多做一点阐释。
传统的非解析几何,基本元素如点、线、角,确定几何图形的关键在于其“相互关系”,几何定理也是在描述其“相互关系”,当然也包括长度、面积、角度等基本数量关系。本质上,几何推导是在推演其相互关系,从已知的角到未知的角、已知的长度到未知的长度,如此等等。通过相互关系推导的困难在于,一旦缺少联系彼此的桥梁,例如少了一条线一个角,那么这样的“相互关系”推导便出现了逻辑断层。辅助线的构造是为了保持这样的相互关系推演的连续性(当然也不是有些评论说的,脑子缓存足够的话直接不画线,其实辅助线画不画出来不重要,最重要的想没想到要用那个辅助线带来的相互关系)。
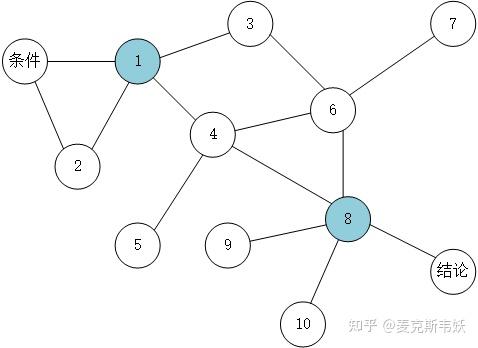
而解析几何做了什么事?费马和笛卡尔的工作,是建立了一个坐标系,早期甚至用的就是一般的斜坐标系。坐标系的意义是什么?是建立了一个“灯塔”标准,所有的几何元素都与之联系,都和坐标产生“相互关系”。那么非解析几何推导中的非中心化的相互关系网络,由于引入了坐标这个与万物都相关的“标尺”,变成了一个“中心化”的相互关系网络。那么,几何推导的路径就变成了先将几何元素信息和坐标标尺联系,然后再通过坐标标尺的转换关系与另外的几何元素联系,由此实现两个独立几何元素的相互联系。
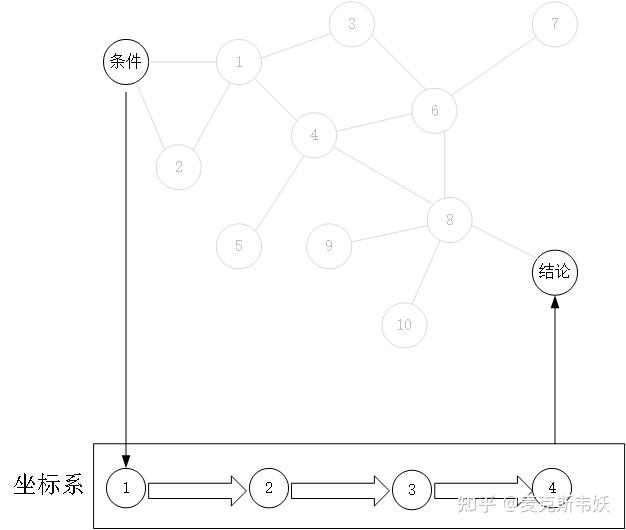
形象点说,非解析几何就像你打电话找一个你不熟悉的人,你可以找你熟悉的人问,然后他找另外一个问,如此询问信息在一个非中心的网络中传递,最后找到这个人,少了一环可能就很难找到了,其中某些人也可能就是找到这个人的中枢关键,这就是辅助线。
而解析几何很简单很暴力,就像你建立了一个认识所有人的电话转接中心,你直接打电话问这个中心,马上就能给你转接你想找到的那个人。
所以,其实解析几何最大的辅助线,是不是就是这个坐标系呢?(哈哈哈哈哈
所以你也能感受到,解析几何不太关注几何元素之间的相互关系,只关注如何代数化(就是如何给话务中心打电话),而后就是更抽象更连续的代数处理,最后再转回几何结论。
举个生动一点的例子,你要判断相隔几万公里的两条线段是否平行,对于非解析几何的话,你非得做点辅助图形将两条线段连起来不可。但是解析几何,你只需要写出坐标,然后比对斜率或者做个向量叉积即可。
或许我阐述的并不能解答关于“推理连续性”的疑惑,只是解释了为何解析几何比普通几何更容易求解,但是解析几何内部的推理连续性并没得到解释。
更高阶的代数定理确实也是由各种不连续的定理构成的,也存在很多惊为天人的构造性定理,尤其是到了高等前沿的数学领域,完全不是简单的解析几何可比的。
基础的代数推理包括一些恒等变形和公式应用,我认为这些都只是代数元素在确定计算法则后的推论,将这些推论记为一些定理后,便变成了一些类似“辅助线”的存在,但是这个“辅助线”是抽象的,但是人脑能够很好记忆,且构造性不强,因此推理连续性很强。(当然也有强构造性的,你面对一堆被打散的代数式要进行因式分解的时候就能深刻感受到。)
人们对于“拆”是逻辑连续的,但是对于“合”是逻辑断裂的,类似的还有求导总比积分简单,这里面有信息论在起作用。因此,在上大学后,你做积分,有时候要“凑”微分,这个可不比辅助线简单;你求微分方程解,观察到特解也不容易。那些证明中云淡风轻的“不难发现”,往往就是代数的“辅助线”,你发现不了,那就GG了。
但是我相信,每个从一种问题到另一种问题的“模式转换”都是在实现一个类似笛卡尔坐标系的功能,提供一种中心化的辅助工具,模式转换本身就是最强大的“辅助线”。例如群环域的抽象,将所有的代数关系和结构合起来研究,再到范畴论更是抽象之抽象。
总结来说,我认为,辅助线是非中心化的几何相互关系网络相互连接的桥梁;而解析几何通过“坐标系”这个“大辅助线”将分散的几何元素中心化地连接起来,而后通过连续性更强的代数推导进行推演,最后再映射回几何元素之间的相互关系。
不过,普通几何和解析几何到底谁更通用,其实不好说,对于那种只有定性关系而没有定量关系的几何问题,其实普通几何的证明更加通用。
例如,要你证明圆周角定理,用解析几何可得假设多少变量:圆半径未知,圆周角的两端点和定点未知,但是却要从繁琐的三角函数推导中得到一个如此简单的角度相等结论,可比普通几何做个简单的圆心角辅助线复杂得多。因此,解析几何更适合拿来做固定结构(坐标)的计算,而普通几何更适合证明“动态”变化中的不变的规律。
之前我的一个回答也涉及了这方面的问题,可以参考。
为什么我觉得初中数学比高中数学难?

 微信扫一扫
微信扫一扫 



