首先,申明一点:
是一个没有商定值的数学表达式。但根据约定,最常见的是将其结果定义为
或将表达式保留为未定义,并根据上下文存在各自的理由。 在代数,组合学或集合论中,普遍认同的值是
,而在数学分析中,表达式通常是未定义的。计算机程序也有不同的处理方式。[1] -- Wikipedia
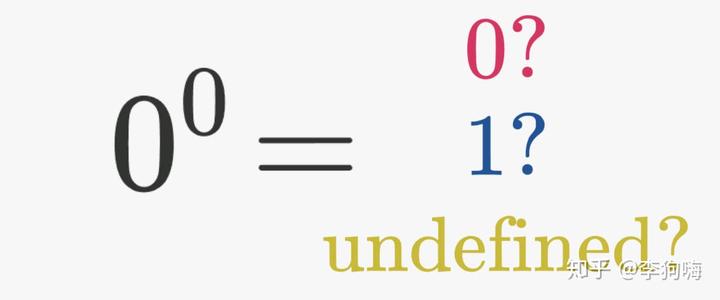
【注意】:下面就只针对 这种情形,借鉴 Better Explain 上的思想[2],用一种通俗直观的方法去理解这样的定义[3]。这也就是写该回答的目的之所在。即:为的是便于直观理解,而不是要去推翻谁。
在我刚学习指数的时候,经常会很狭义地去理解指数的定义,即认为:指数就是连乘,这对于特殊的情况来说(指数是非零整数时),是一个不错的解释,连小学生都能够很快理解这个概念。但是随着时间的推移,见到的多了,就会在计算过程中怀疑这种连乘的方法是否是失效了,因为你看到
之类的东西,甚至是更奇怪的,例如
,我记得高中时老师对于这个概念一笔带过,就说这是它的“定义”,但对我来说我是很难接受这个奇怪的定义的。
我们最先接触到的基本数学运算是加减乘除,“加减”与“乘除”分别属于数学中的第一级和第二级运算,详情请见《如何理解对数?》。在刚开始学习算术的时候,老师会教我们通过数指头的方法来完成加法的计算(例如
),以及通过重复加法来实现乘法计算例如(
)(当然有的老师只会教乘法表…)。不过不管怎么说,这一切看起来似乎都挺自然的。
但上述方法当然也只是针对简单或者说特殊的情况,当包含有负数或者无理数的时候呢,这种方法显然就行不通了。加减乘除本身并没有问题,问题在于对算法的理解上太狭隘,不具有普适性。
为了使算法的定义具有普适性,不应单纯地用计数来实现加法,而是将其看做是在一条直线(数轴)上点的位置变化。这种位置可以是负的(如
),可以是在某些数之间(例如无理数),或者是在其他的维度上(例如虚数
,详情请见“虚数 i 是真实存在的吗?还是被人们创造出的数学工具?”)。
那么,更加广义的算法思想应当是:将加法视为是一种在数轴上的“滑移”,例如:
就是向右滑移
个单位。乘法就是“缩放”,例如:
就是扩展到原来的
倍。
那么指数呢?
算法 狭义定义 广义定义
加法 重复计数 滑移
乘法 重复相加 尺度缩放
指数 重复相乘 随时间的增长
关键词:随时间的增长!随时间的增长!随时间的增长!(重要的话说三遍)、
举一个具体的例子,对于指数
,可以用以下的步骤进行分析(这可能是个笨办法,但对于理解问题有益):
设定初始值为
个单位量(指数前面的因子,指数
前面的因子为
,指初始值为
个单位数量,即
,因为乘以
不影响结果,所以可以省略不写了,但是要知道它的存在),将其记为:【
】。
设定每增长
个单位时间,量就增长到
个单位时间前的
倍(即指数的底数),将其记为:【
】。
设定增长时间
个单位时间(即指数的幂),将其记为:【
】。
对于以上过程,在数学上可以给出通式,其中【
】为指数运算的结果:
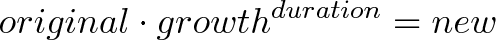
或者写为:
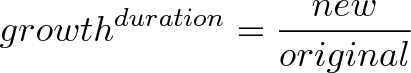
就拿上面的
的例子来说,底数
指的是单位时间数量增长的倍数(或称为增长倍率);而幂
指的是数量增长的时间;
为初始数量。
对指数的这种“增长”的理解不同于乘法的尺度缩放,乘法会给你一个非常明确的尺度因子,你一眼就可以看出其会将初始数量缩放到一个什么样的尺度上去。但是对于指数,就没有一个这样明显的缩放因子,因为它代表的是一种“增长”,相比于乘法(直接缩放得到结果),指数更强调“过程”。这个思想很重要,因为自然界中大多数事物都处在一种“无意识的增长”当中!
例如,细菌并不会计划着自己一天分裂一次,它只会以其自己的方式进食并增长、分裂,而且初始的细菌数量越多,其总量的增长速度也就越快,初始数量就体现在上式的“
”中,初始数量对最终结果的影响表现为尺度上的缩放,即乘法的算法思想。
为了得到它们增长的最终结果,我们需要知道它们当前的增长倍率以及增长的时间。所以指数操作就可以用简单一句话概括:“以某个初始数量(
)为起点,以一定的增长倍率(
)增长,等到了设定的时间(
),看看增长到了多少(
)”。
分数幂的解释
就前面提到的分数幂问题,可以用广义的指数算法思想进行解释。例如
,既然
表示初始值为
,单位时间增长率为
,增长
个单位时间后的值;
表示初始值为
,单位时间增长率为
,增长
个单位时间后的值。
那么,
当然就可以理解为初始值为
,单位时间增长率为
,增长
个单位时间后的值了。如果能将这个概念告诉斯蒂菲尔(Michael Stifel)[4],或许他将会成为发现对数的第一人吧,因为他正是因为那个时代的人们还无法理解分数幂的概念而放弃了对“对数概念”的进一步探究。
指数相乘计算
现在考虑一种情况,就是如果两次增长率相同的增长“无缝连接”,即一次增长紧接着上一次增长,例如,以单位数量为初始值,以一定的倍率增长,先增长 2 个单位时间,再在此基础上增长 3 个单位时间,问题就可以用下式表示:
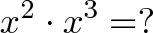
实际上和以单位数量为初始值,以一定的倍率增长,一共增长
个单位时间所得到结果是等价的。写成通式就是:
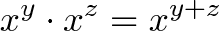
这就底数相同(即增长率相同)的指数的乘法法则,即同底指数相乘等于底数不变,幂相加。
指数的开根计算
假设现在初始值为
个单位数量,增长率为
,那么增长
个单位时间后的结果为:
。
那么,对于上面的情况,其中间时刻(
个单位时间时)的数量是
。
如果重复两次
个单位时间的增长,并运用上面说过的指数相乘运算方法,会发现:
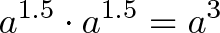
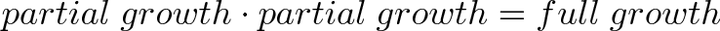
用一句话描述就是“半个周期的增长结果乘以半个周期的增长结果等于整个周期的增长结果”。这也意味着半个周期的增长结果是整个周期增长结果的平方根。即,增长时间减半相当于开平方操作。
那么,如果将时间等分为
份,并让
次增长接连发生,得到的将是:
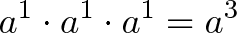
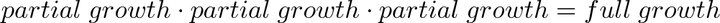
显然,得到结论是
个周期的增长结果是整个周期增长结果的
次方根。可以想象得到,如果将增长时间等分为
等份,那么
个周期的增长结果将是整个周期增长结果的
次方根。
负指数的解释
如果将幂视作时间,那么负的时间直观上其实就可以理解为“时光倒流”。如果正常情况是以一定增长倍率增大,那么“时光倒流”就指的是以一定的倍率缩小。
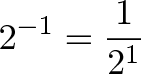
上式的含义是:“一个单位时间前的数量是当前数量的
”。其实,在指数函数
的图像中中任意间隔单位时间的两个点都满足上面的比例关系。
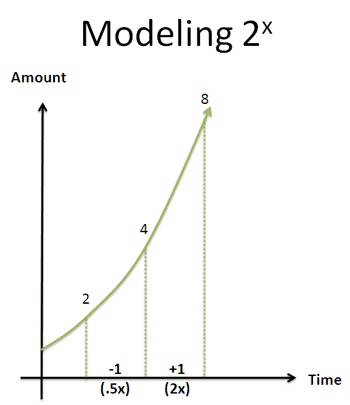
0 次幂的计算
那么,当幂为
代表什么?先举个例子,例如
的意义。它可以解释为:初始量为
个单位数量,增长倍率为
,增长了
个单位时间。也就是说,没有给其增长的机会(时间),数量当然保持着原样,即为
个单位数量或直接写成
。其他情况(除了底数为
的特殊情况,下面单独讨论)都可以用这样的方法解释。
解释 (其中,
)
即指数的底数为零的情况。表示的是初始量为 1 个单位数量,增长倍率为
,增长了
个单位时间。可以理解为一旦给其时间增长,就会变成
。如果无法一下理解,就先假设
,即
,表示的是:
个单位时间后会变为
。那么现在将
个单位时间分为
个等份,其中
,那么
为
的
次方根,当然也为
,所以,无论幂
多么小或者说无论增长时间多么短,只要幂不为
,底数为
的指数都为
!
最后看看
的
次方,这个现在终于可以解释了。表示的是初始量为
个单位数量(注意其可以看做
),增长倍率为
,增长了
个单位时间。虽然上面说了只要给其增长的时间,它就为
,但是现在的情况是:并没有给初始值发生这种增长的机会!
所以,不管以多少倍率增长其实都无所谓,任何形式的增长都没有发生,最终结果就是初始值
个单位数量或直接写为
,所以有
。
另外,推荐一下我的知乎专栏,里面有很多其他数学概念的直观解释:
直观の数学

 微信扫一扫
微信扫一扫 



