回答已更新,在下面加了两个电磁学的例子。
谢邀。
我个人认为积分在物理上的应用标志着物理学思想的一次革命。积分在物理公式中的应用体现了一种优雅的物理思想:当我们在面对一个复杂而难以入手的问题时,可以考虑把这个大问题分成若干个容易解决的小问题并解决这些小问题.同时,积分在复杂的物理系统和简单的物理系统之间搭建了一座桥梁.
举个很简单的例子,我们需要知道一个质点运动的总路程.我们已有的信息是这个质点运动的速度
随时间
变化.但是这样的问题在当时是很难入手的,因为人们只知道当速度恒定时,在一个时间间隔
物体行进的路程
. 聪明的物理学家们试图将这个复杂的问题与我们已知的这种非常简单的情况建立联系.于是他们说:当我的时间间隔
足够小的时候,速度
几乎没有变化,那么这个质点在这一段很短的时间内走的路程是容易求的,就是
.由于极限确保了我们的结果是精确的,我们现在把无限多无限小的精确情况加起来,就得到了这个复杂情况的解,即
.
再举一个例子,考虑一个质量为
质点的转动惯量,物理学家把这个转动惯量定义为
,其中
是质点离旋转轴的距离. 如果我们考虑一个由无数个质点构成的一个复杂的物理系统,比如一个很薄的绕中心转动的圆盘(半径为
,质量为
),那么我们该怎么求整个盘子的转动惯量?
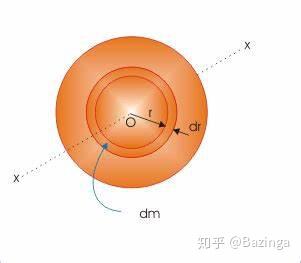
物理学家说,我们一下子不知道这么复杂的问题怎么求,但是我们还是可以把它分成无数个简单的问题. 我们知道,距离旋转中心
有相同距离
的所有质点都有相同的转动惯量,于是我们可以把整个盘子分成无数个无限小的圆环,这些圆环的宽都为
,无数个这样的圆环的宽组成了更个圆的半径
. 还是考虑其中的一个情况,然后将其推广即可. 假设有一个圆环的内环半径为
,我们怎么先求这个圆环的质量,这很好求,就是整个盘子的质量乘上这个这个圆环占整个圆的面积比就好,即
,那么这一个微小的圆环有一个微小的转动惯量,即
,由于每一个微小的圆环都无一例外都遵守这个表达式,所以解决了所有的简单的情况,现在把这些简单的情况拼凑成原来的复杂情况就可以了.
.
=================更新:==================
下面举两个电磁学的例子.
1:求一个无限大的平面在距离平面
的一点
产生的电场大小.
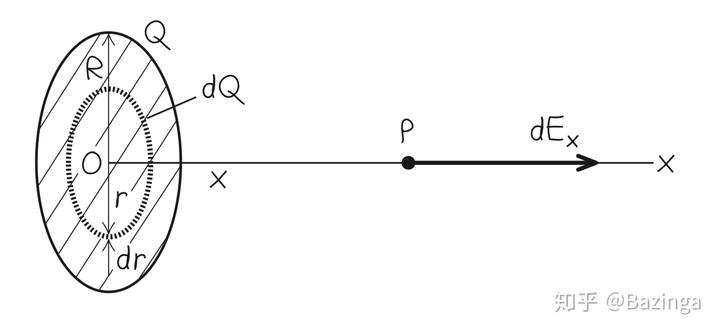
首先构造一个微小的圆环,该圆环由半径分别为
的两个同心圆构成. 根据对称性容易发现,该圆环上的任意一个微小的面积
在
点产生的电场只有
方向的分量有效,因为对于任意的
都可以找到一个对称的等大的面积,其产生的电场与
产生的电场在竖直方向抵消. 那么由这块面积产生的电场就是
.其中
为
与
连线与
轴的夹角.
那么
当这个圆环上所有的
贡献的磁场加起来,
. 其中
是电荷密度.
现在我们可以求这个无穷大平面在
产生的电场了. 由于平面是无穷大的,所以
从 0 取到无穷大.
2.除了计算之外,微积分,尤其是物理里面常用的微元法,可以让我们得到一些有用的结论,比如我们可以从一个点电荷在磁场中受到的洛伦兹力,推导出一段导线在磁场中受到的作用力.
首先一个电荷受到磁场的力是
那么一个微小的电荷受到的力就是
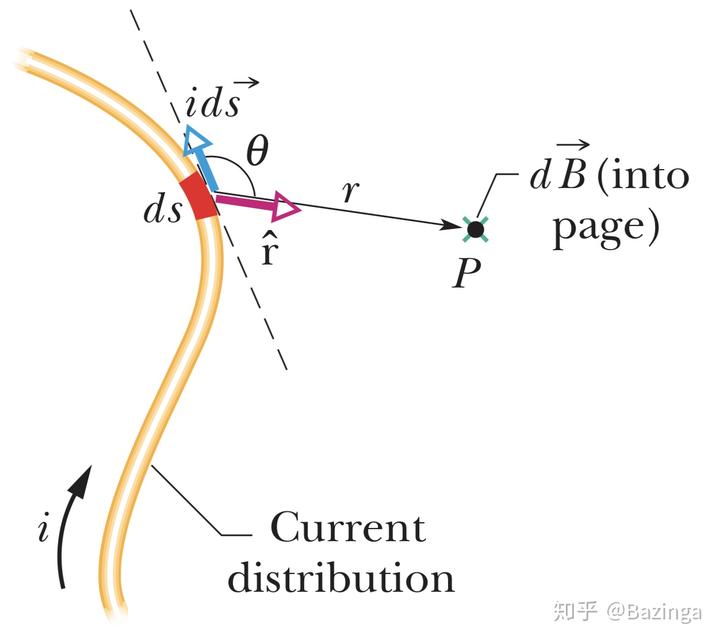
现在我们可以通过微积分进行一些简单的变形. 我们知道电流等于电荷的变化,即
,所以我们可以把微分形式写成
.
那么整条导线受到的力就可以写成
如果导线始终与磁场垂直,那么
=======================================
所以,为什么大学的物理公式基本上都需要用到积分呢?因为我们解决的问题越来越复杂,初中高中学习的简单模型已经无法解决这些情况,但是我们仍然可以把复杂的问题拆解成一个个容易解决的小问题,逐个击破这些小问题,而最后积分是把这些简单的问题重新拼凑成复杂问题的一个工具.

 微信扫一扫
微信扫一扫 



