为什么玻璃杯倒水的时候水会沿外表面流下而不会直接掉下?_网络百科

从日常生活现象提炼物理问题，给题主 A+！善于思考！

这个现象叫茶壶效应(teapot effect)。当然不仅限于茶壶。杯子，碗，喷泉，下雨的屋檐。。。

很早就有人思考这个问题。例如上面这个图，来自 1956 年Physics Today杂志上的一篇文章^[1]。以色列海法技术研究所的 Markus Reiner 教授做了一系列实验来探究茶壶效应背后的物理。那么茶壶效应说的是什么？上面这个图描绘的是当水注入茶壶内以后，水从茶壶嘴流出。从左到右逐渐增加注入水的流速。我们知道当我们倒茶的时候你应该看到的是类似于弹道曲线的抛物线。但是第一幅图显示的是当流速很小的时候从茶壶嘴溢出的水沿着茶壶嘴外壁流到茶壶底部，像是黏在了壶身上。第二图稍微增加注入水的流速，流出的水变成了两部分，一部分仍然沿着壶嘴外壁流到壶底，另一部分形成了向下流的水柱。但是仔细观察你会发现这个水柱不是垂直向下的而是向壶身一侧弯曲而不是向另一侧喷出以形成弹道曲线。再增加水流流速第三图，黏在壶身上的水流没有了只剩下水柱，但是水柱的流向依然不是我们预期的。最后一图当流速足够高以后水柱才不再弯向壶身。

他之所以做这个研究是因为他说，当有人问他这个问题的时候，他想当然的认为是表面张力。然后他问了很多物理学家，大家的回答基本上一致为表面张力，或者毛细管效应（一回事）。本人也在知乎上搜了下跟这个问题类似的问题，的确大多数的回答是表面张力。（如果你直接搜茶壶效应那当然是另一回事了。）但是大多数人从来都是想当然了，背后的物理肯定不是仅仅表面张力这么简单。Markus Reiner 没有给出令他自己满意的物理解释。但是他在文章中说到希望这些实验能够引起别人的注意以期能有人给出令人信服的物理解释。

这里简要介绍下 Markus Reiner（马尔克斯·雷纳）何许人也。Markus Reiner 是流变学的奠基人物之一，流变学的名称（Rheology）都起源于他的建议。此外，他的学术贡献还包括 Buckingham-Reiner 方程，Reiner-Riwlin 方程， Reiner-Rivlin 流体，以及流变学一个重要参 Deborah number 底波拉数。当然还有茶壶效应。

我找到了一个令人信服的解释，一篇 2010 年发表在物理学顶级期刊（有没有之一都不重要）物理评论快报（Physical Review Letters）上的文章^[2]。以下内容除了必要的背景知识介绍和简要的注解，大多数翻译摘选自参考文献^[2]。

先上结论（文章摘要部分）：研究团队发现物体表面的可湿性（wettability，或者叫可浸润性，跟亲水性疏水性同理）是茶壶效应的关键因数。采用超疏水性材料可以极大的抑制茶壶效应。茶壶效应背后的物理是流体惯性作用和毛细效应的耦合(inertial-capillary coupling)。他们的提出的物理模型成功的解释了茶壶效应对材质可湿性、流体速度、固体表面边缘圆角的曲率半径的依赖关系。

茶壶效应。视频来自参考文献[2] https://www.zhihu.com/video/1213778268606173184

上面

$\uparrow$

这个视频茶壶壶身上镀上一层亲水材质，可以看到控制水流后水会沿着壶身流向壶的底部，清晰的展示了茶壶效应。

下面

$\downarrow$

的视频你会发现不管水流是快是慢，水都是垂直向下流，并没有黏在壶身上。茶壶效应被明显的抑制。原因在于壶身采用了超疏水性材质。（后面会介绍材料的亲水性和疏水性）。

超疏水材质对茶壶效应的抑制。 https://www.zhihu.com/video/1213783548932792320

下面我们细致的看他们是如何研究这个问题的。基本的实验方法如下图 2a 所示。水柱以速度

$U$

向下冲击圆盘。水柱的直径小于圆盘的直径。水柱被圆盘阻挡后会向外流出，到达圆盘边缘，然后以一定角度

$\Psi_0$

落下。圆盘边缘的圆角的曲率半径为

$r_i$

。圆盘材质的可湿性由不同化学工艺和材质来控制。对应不同的材质接触角。接触角是标志材质亲水性或疏水性的特征参数。接触角越小材质越亲水越容易被润湿（可湿性高），反之接触角越大材质越疏水。他们实验中材质的接触角可从

$10^\circ$

（超亲水）到

$175^\circ$

（超疏水）变化。

这里简要补充下接触角的概念以及对材料可湿性的影响（接触角维基百科戳这里）。接触角（Contact angle）是指在液体或气体界面接触固体表面而形成的夹角。比如液滴接触固体表面的那部分的切线方向与固体表面的夹角。如果材料为光滑平整的亲水固体，液滴会平铺在材料表面，接触角接近 0 度。如果材料为疏水材质，则接触角可以大于 90 度，液滴保持其原状。超疏水的材料大家一定都见过，比如超级给力的荷叶，或者大部分的雨伞以及防水冲锋衣。荷叶的神奇在于其微观结构上有许多小突起，极大的增大了接触角，因此表现出极强的疏水性。

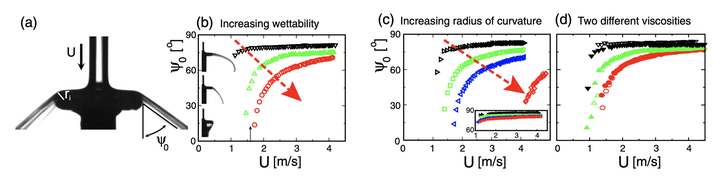
OK，回到上面的实验。图 2（b-d）展示了实验结果。图 2b，水流从圆盘上出射的角度随材质可湿性（材料接触角）的变化。从上到下黑绿红三色分表代表的材质接触角为 175 度、115 度、10 度。很明显黑色曲线的材质为超疏水性（接触角接近 180 度）出射角度接近 90 度，几乎是平行于圆盘出射，没有茶壶效应。而红色代表的亲水材质对应的出射角度最小，表现出茶壶效应。图 2c，圆盘圆角曲率半径对出射角的影响（这里使用的是亲水性材质）。图 2c 黑绿蓝红四条曲线对应的曲率半径分别为 0.03mm、0.5mm、1mm，2mm。显然边缘圆角的曲率也会影响茶壶效应。但是曲率带来的影响不是主要的。原因在于图 2c 里的小插图。小插图里面改用疏水材质后，四条曲线几乎重合，都对应大的出射角，也就是在疏水材质条件下，曲率变化不再对茶壶效应起显著作用。最后图 2d 是排除了很多人可能认为材料的黏性对茶壶效应的影响。这里一共六条曲线，所有的曲线对应的圆角曲率是相同的，黑绿红对应的接触角依然分别是 175 度、115 度、10 度，不过实心数据点和空心数据点对应的材料黏性不同。实心点对应的是低黏性的水，而空心点对应的是高黏性的水和甘油混合物（water-glycerol ）。很显然，对于相同的接触角，实心曲线和空心曲线几乎是重合的，代表的意思是材料黏性对茶壶效应无影响。

最后，茶壶效应的临界条件也是能从实验上给出的。图 2b-d 都是入射水流流速对出射角的影响曲线。当入射水流流速低于一定阈值

$U_c$

的时候，水流不会从圆盘出射，而是沿着圆盘下表面，如图 2b 里面的插画所显示。三幅插画从上到下对应箭头与三条曲线相交处的情形。由于材质的接触角逐渐减小（可湿性逐渐增大），抑制茶壶效应的阈值流速则相应的逐渐增大。

到了这里可以小结下了。影响茶壶效应的三个关键因数：

流体的流速（惯性作用）
壶嘴（边缘）的弯曲程度
材质的可湿性（亲水性或疏水性，这个因数是这篇文章的关键点）

其实到了这里还没有上真正的物理分析呢！

可是我累了，先睡觉了，明天早上起来再更后半部分（无聊的物理分析）以及有意思的新发现。

既然大家赏脸那就更文章后半部分的硬核物理。

首先物理机制前面已经明确表达了：背后的物理是流体惯性作用和毛细效应的耦合。

这里先补充必要的背景知识。

惯性作用：惯性力（inertial force）（维基百科戳这里）是指当物体加速、减速或改变方向时，惯性会使物体有保持原有运动状态的倾向，若是以该物体为参照物，看起来就仿佛有一股方向相反的力作用在该物体上，因此称之为惯性力。惯性力实际上并不存在，实际存在的只有原本将该物体加速的力，因此惯性力又称为假想力。它的概念的提出是因为在非惯性系中，牛顿运动定律并不适用。但是为了思维上的方便，可以假想在这个非惯性系中，除了相互作用所引起的力之外还受到一种由于非惯性系而引起的力——惯性力。加入惯性力后，牛顿运动定律成立。例如，当公车刹车时，车上的人因为惯性而向前倾，在车上的人看来仿佛有一股力量将他们向前推，即为惯性力。然而只有作用在公车的刹车以及轮胎上的摩擦力使公车减速，实际上并不存在将乘客往前推的力，这只是惯性在不同参照系下的表现。
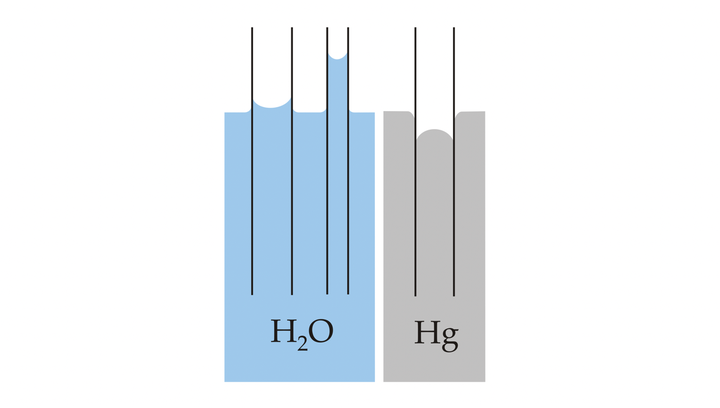
毛细效应：（或者叫 capillary action, capillarity, capillary motion, capillary effect, wicking，建议参考英文版维基百科戳这里）。请注意这里没有表面张力（surface tension），待会就有为什么。毛细(管)效应指的是在毛细管内部流体能够不借助外力甚至克服重力而流动的现象。毛细效应的物理机制是液体和固体界面上分子间的相互作用力。如果毛细管的内径足够小，那么表面张力(本质是液体分子间的结合力 cohesion force)和液体分子与固体分子之间的粘和力(adhesive force)的合力使得液体表现出毛细效应。划重点：这里表面张力只是毛细效应的一部分。而毛细效应只是茶壶效应的一部分，因此才有本文开头说茶壶效应不仅仅是表面张力这么简单！毛细效应的一个经典图如下：毛细管中的水和水银的液面都表现出了典型的毛细半月(capillary meniscus)凹陷或凸起。不同的是水银本身的原子结合力(表面张力)大于水银与管壁之间的粘合力，因此水银液面中央会比四周凸起，这和毛细管中水的状况恰为相反。

再回到茶壶效应。

我们来看研究者们是怎么建立物理模型并得到合理的物理解释的。首先说明，严格的预测出射水流的角度和速度需要严格求解惯性流体动力学方程(欧拉方程)。感兴趣的请看这里欧拉方程。严格求解流体力学方程是一件很困难的事情，因为流体力学的问题往往都是变态难。比如物理学至今未解之谜湍流。关于湍流有一个经典的段子：量子力学大牛海森堡说如果他有机会见上帝，他要问上帝两个问题：相对论和湍流。海森堡说：“我真的相信上帝也只能对第一个问题给出答案”。足见湍流有多复杂。When I meet God, I am going to ask him two questions: Why relativity? And why turbulence? I really believe he will have an answer for the first.

扯得有点远，总之严格求解欧拉方程是不现实的，那就做一些合理的近似和简化。（这是物理研究的合理策略，复杂问题简单化以抽象出简单的物理模型。得到物理模型后对问题作出预测然后跟实验对比以检验模型正确与否。）

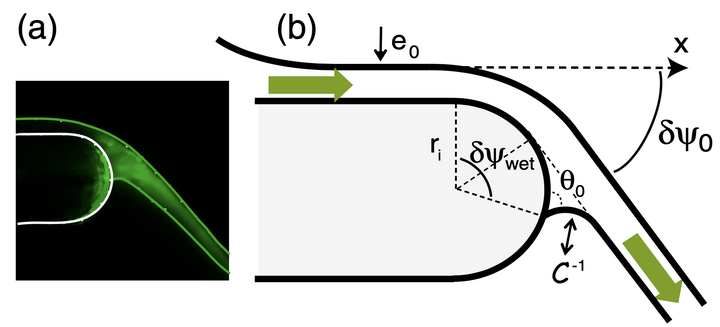
简化的基本物理模型见下图 5 所示。考虑流体层的动量平衡。流体的出射对应的是流体动量通量的变化，这个动量通量的变化由流体指向固体的黏性附着所补偿。考虑比较大的流体流速，对应的流体出射方向与水平面的夹角

$\delta\psi_0 = \frac{\pi}{2}-\psi_0$

很小。这个偏转角度对应的流体动量通量变化为

$\mathcal{D} = \rho_w U^2e_0(1-\mathrm{sin}\psi_0)\approx\frac{1}{2}\rho_wU^2e_0\delta\psi_0^2$

。然后动量平衡中粘合力的贡献变现为液体压强的降低

$\Delta P$

，压强的降低是由于流体层的弯曲。这个弯曲表现为接触面的浸润区域

$\mathcal{A}_{wet}\approx r_i\delta\psi_{wet}$

，由此可以给出粘合力为

$F_{adh} \sim \Delta P\times \mathcal{A}_{wet}$

。这个力在水平方向 x 上的分力是

$F_{adh}^x\approx\mathcal{A}_{wet} \times\Delta P\times\frac{\delta \psi_{wet}}{2}$

。压强变化

$\Delta P$

是由于流体弯曲造成，所以可以根据伯努利原理求出，

$\Delta P \approx-\rho_wU^2e_0/\mathcal{R}$

，这里

$\mathcal{R}$

代表的是流体弯曲的曲率半径。

$\mathcal{R}$

的大小为

$\mathcal{R} \approx r_i+\frac{1}{2}e_0$

。下面这个模型的关键是联系浸润区域

$\mathcal{A}_{wet}$

(粘合力)和毛细效应半月形区域。首先半月形区域的曲率为

$\mathcal{C}$

，对于特定的压强变化

$\Delta P$

曲率为定值，

$\mathcal{C} = |\Delta P|/\gamma$

，

$\gamma$

为液体和气体界面的表面张力。将这个半月形近似看成圆弧可以得到

$\delta\psi_{\mathrm{menisc}}^2 = 2\mathcal{C}^{-1}/r_i\times(1+\mathrm{cos\theta_0})$

。由此最终得到浸润区域

$\mathcal{A}_{wet} = r_i\delta\psi_{wet}$

，这里

$\delta\psi_{wet} = \delta\psi_{0}+\delta\psi_{\mathrm{menisc}}$

，

$\delta\psi_{\mathrm{menisc}} = [2\gamma(1+\mathrm{cos}\theta_0)/r_i|\Delta P|]^{1/2}$

。有了这些就可以写出动量平衡方程：

$\frac{1}{2}\rho_wU^2e_0\delta\psi_0^2\approx\frac{1}{2}|\Delta P|r_i(\delta\psi_0+\delta_{\mathrm{menisc}})^2$

。最终推导出

$\begin{equation} \delta\psi_0 = \sqrt{\mathcal{F}[\frac{r_i}{\mathcal{R}}]\frac{(1+\mathrm{cos}\theta_0)}{We}} \end{equation}$

这里

$We = \rho U^2e_0/\gamma$

为特征常数韦伯数(Weber number，代表惯性力和表面张力效应之比，韦伯数愈小代表表面张力愈重要，譬如毛细管现象、肥皂泡、表面张力波等小尺度的问题。一般而言，大尺度的问题，韦伯数远大于 1.0，表面张力的作用便可以忽略)，

$\mathcal{F}[r_i/\mathcal{R}]\simeq 2(1-\sqrt{r_i/\mathcal{R}})^{-2}$

为特征几何因子。

上面的公式就是这个物理模型的给出的推论了。下面检验探讨下这个模型是否符合前面的实验结果。

首先，这个推论显示茶壶效应的确依赖于圆盘表面特性。两层意思，1)表面的几何特性，即 $\mathcal{F}[r_i/\mathcal{R}]$ 。2)可湿性，也即接触角 $\theta_0$ 。
其次，这个推论能够完全呈现实验结果图 2 中的所有结论。出射角度 $\psi_{0}=\pi/2-\delta\psi_0$ 的确随流体速度（ $U$ 或者 $We$ ）的增大而增大；出射角度也的确随接触角 $\theta_0$ 的增大而增大；出射角度的确随圆盘圆角的曲率半径 $r_i$ 的增大而减小。
最后，这个模型也能间接的推论出茶壶效应阈值流速的存在。 $We_c \propto \frac{r_i^2}{e_0^2}(1+\mathrm{cos}\theta_0)$ 。

到了这里实验现象、物理解释都有了，一个好的工作已经完备了。但是还是可以有有趣的应用。这个工作已经清楚的阐述了材料特性尤其是可湿性对茶壶效应的影响。那么如何有效的控制茶壶效应？除了实验本身涉及到的选择不同接触角的材料以改变材质的亲水性与疏水性，以及改变材质的几何特性如圆角曲率，还可以有更有效的控制方法。比如，相比于特定材质的特定可湿性，还有一个电湿性(electrowetting)的概念可以动态的改变材质的可湿性。电湿性说的是在材质表面施加电压将材质电极化以改变材质的接触角。施加不同的电势则可对应不同的接触角，因此将会造成不同程度的茶壶效应。

电湿性是对评论区对于最后一个视频水幕突然消失的解答。最开始没有施加电压，材料的接触角很大表现为很强的疏水性，形成水幕。当突然施加 300V 的电压后将接触角减小为 60 度左右，材质表现为亲水性，水幕消失。

改变电势控制茶壶效应。 https://www.zhihu.com/video/1214039396099817472

！！！！！！！！

更着这篇回答的同时收到邮件弹窗，我的 PRL 接收了

！！！！！！！！

再更一下。PRL 接收的时候太兴奋了，本来打算放的另一个有趣的实验忘掉了^[3]。去年的文章，同样发表在 PRL，同样是惯性作用和毛细效应的耦合机制，见下图 6。

螺旋水柱！

实验中以一定角度将特定流速的的水柱掠入射垂直玻璃柱。玻璃柱的接触角约为 30 度，为亲水性材质。水柱直径 0.5mm，玻璃柱直径 3mm。图 6b 最左边当流速太高时水柱擦着玻璃柱飞出，没有弯折。然后随着流速逐渐减小，水柱弯折逐渐显著，逐渐表现出茶壶效应（这跟上面 2010 年的 PRL 结论一致）。当流速降至 0.5mL/s 时（右起第二图），水柱不能脱离因而以螺旋结构缠绕在玻璃柱上。此外，当又重新增加流速后，螺旋结构并没有消失（见最右图，注意最右图的流速比第二三图都高，本不应该有缠绕），说明这个现象具有一定的滞后性。