先考虑最简单的情况,只从右边增加数字
由于每一层都是质数,所以我们可以从基本的质数开始,构造一个「质数池」。每次从池中取出一个质数,增加一位数字,看看哪个是质数。是的话就扔到质数池中。
这样不断迭代,就可以获得很多这样的数。这种迭代过程也很明显会产生一个树形结构:
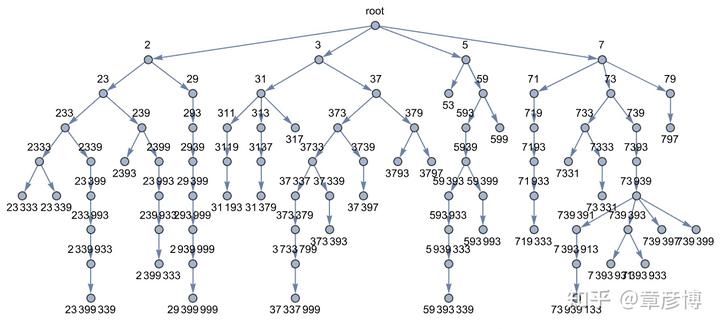
Mathematica 代码如下:
LongerPrime[n_] := Select[Table[10 n + i, {i, 0, 9}], PrimeQ]
current = {0};
tree = {};
Do[
next = LongerPrime /@ current;
tree = Flatten[tree~Join~(Thread /@ Thread[current -> next])];
current = Flatten@next;
, 13]
g = Graph[tree /. {0 -> "root"}, VertexLabels -> "Name",
GraphLayout -> "LayeredEmbedding"]
这样的质数数量有限,只有 83 个。
或者也可以只从左边增减数字
修改代码:
LongerPrime[n_] :=
Select[Table[
FromDigits@
Insert[Piecewise[{{{}, n == 0}, {IntegerDigits[n], True}}], i,
1], {i, 1, 9}], PrimeQ]
跑四层:
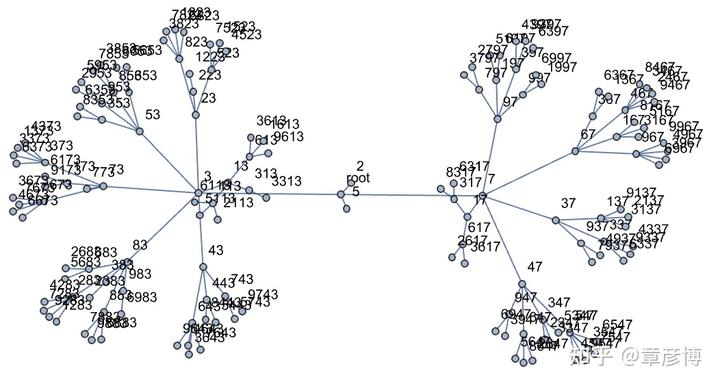
跑 24 层之后就不会有新的素数了,一共 4260 个:
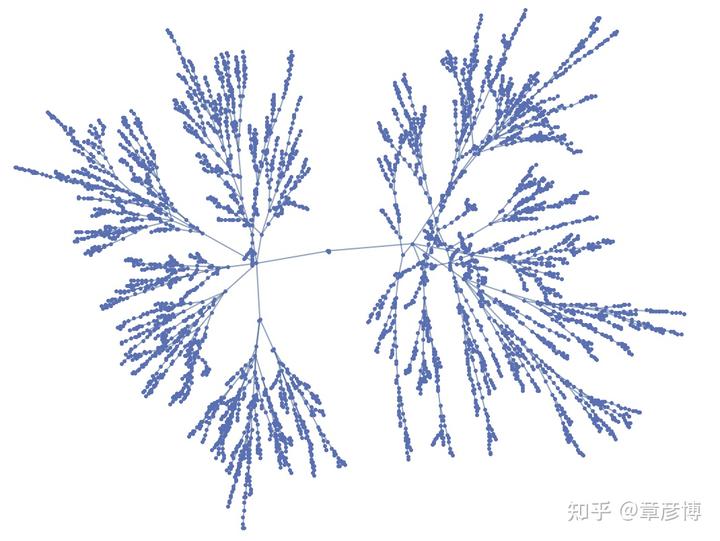
再考虑更复杂的情况——可以在任意位置增加质数
我们需要修改 LongerPrime 函数:
LongerPrime[n_] :=
Select[Flatten[
Table[
FromDigits@Insert[IntegerDigits[n], v, i], {v, 1, 9}, {i, 1,
Length[IntegerDigits[n]] + 1}]~Join~
Table[
FromDigits@Insert[IntegerDigits[n], 0, i], {i, 2,
Length[IntegerDigits[n]]}]], PrimeQ]
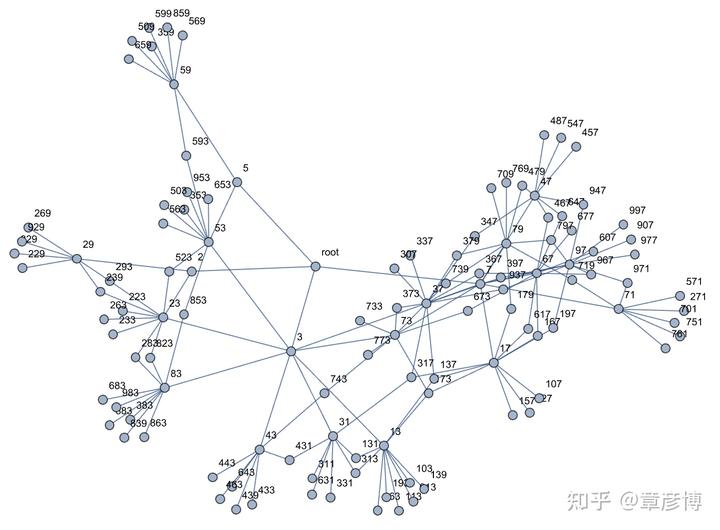
数量多了很多,而且也不是树的结构了。
但如果把题主的意思理解为「去掉任意一位之后,剩下的还是素数,而且仍然具有这个性质,直到一位」。那这样的数就很少了。同样用迭代的方法搜索,我们还要求新搜到的数字,丢掉任意一位之后,都已经包含在之前搜到的数字集合中了。我们需要这样修改代码:

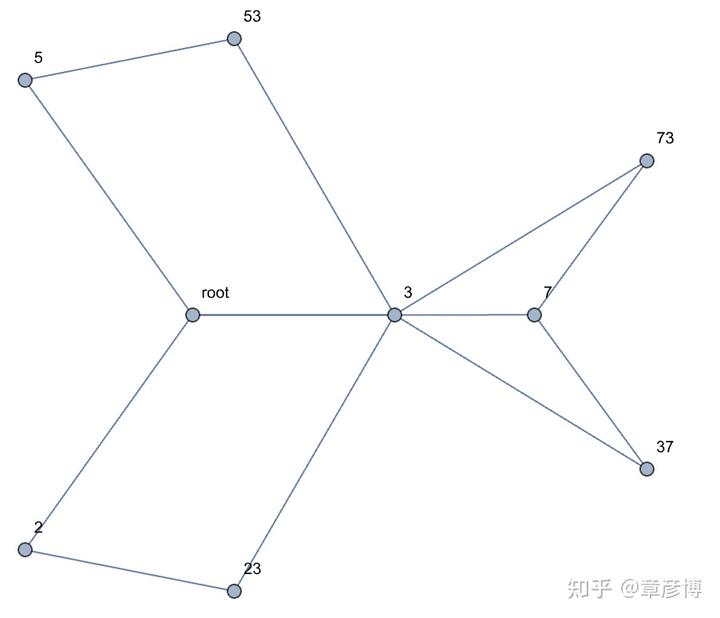
除了个位数,只有 23、53、73、37 四个数字符合要求。

 微信扫一扫
微信扫一扫 



