在波相消的位置消失的能量,转移到了波干涉相长的位置。
为了比较形象直观,我们用光作为例子。光以波的形式在空间中传播,使得其发生干涉或者衍射现象。它们在某些地方相消,在某些地方相长,但总的能量总是守恒的。我们可以形象地理解为:干涉、衍射等效应把能量从暗条纹处转移到了亮条纹处了。
在大自然中,光存在衍射、干涉等现象。这些现象中就包含了光的“相消”问题。在高中的时候我们便已经学习过能量守恒定律。其表述为:能量守恒定律是自然界普遍的基本定律之一,能量既不会凭空产生,也不会凭空消失,它只会从一种形式转化为另一种形式,或者从一个物体转移到其它物体,而能量的总量保持不变。这个问题中,若光发生了干涉,使得光在某处出现暗条纹,我们自然而然地认为能量“消失”了。但其实不然,光的能量只是从一个地方转移到了另一个地方。
我们举一个著名的例子:杨氏双缝干涉实验
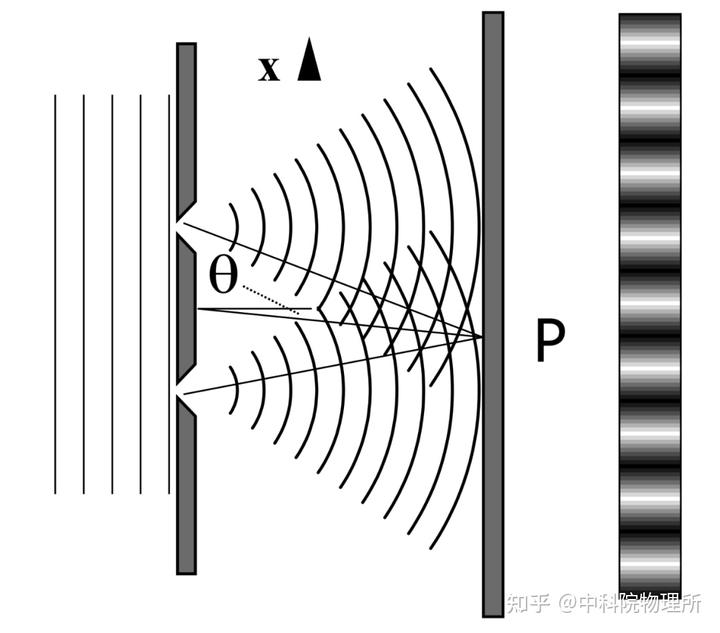
同一光源(保证初始的相位相同)的光穿过挡板的两个缝隙,成为两束光,分别到达屏幕上。
当两束光到达同一个点时,它们俩走过的路径不一样,在相位上存在一个差别,使得它们在某些地方出现相消,在某些地方出现相长。从而人们在屏幕上观测到明暗相间的条纹。相消的地方出现暗条纹,能量密度低,相长的地方出现亮条纹,能量密度高。如果我们把每一个点的能量求和,那么不发生干涉现象和发生干涉现象的总能量是一样的。我们可以形象地理解为:干涉效应把能量从暗条纹处转移到了亮条纹处。
为方便我们用两束有角度的平面波干涉作为例子。
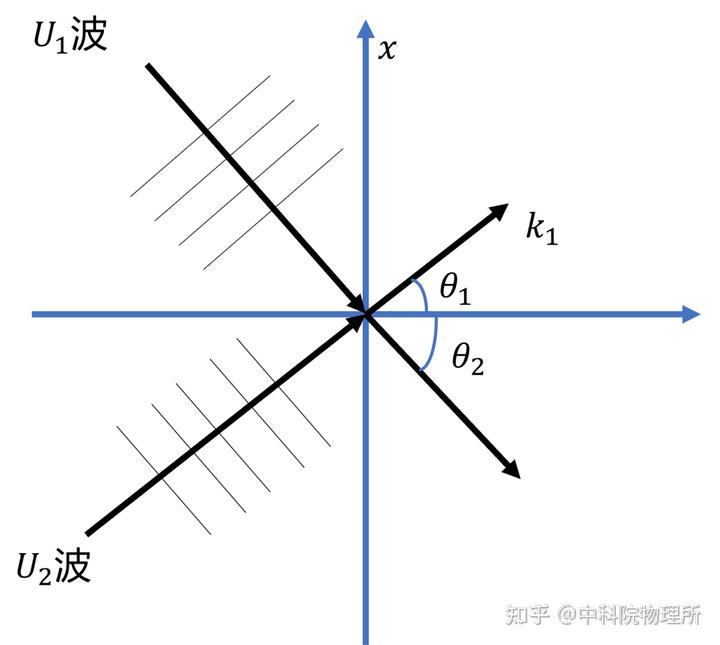
一个点上的光强正比于复振幅的模平方的,即
空间中的平行光的复振幅分布可表示为
其中
是光源到空间中某点的矢量。再由叠加原理可知,光在空间中某点的复振幅是可以直接相加的
对上面的式子取模平方,可以得到
因此,我们可以得到两束频率相同的平行光干涉后的光强表达式为
其中
为衬比度,相位差
为坐标
的函数
我们能够直观地画出光强在空间上的分布曲线

可以清晰的看出,相消的位置与相长的位置的光强的总和并没有变,他们的和正好与没有干涉效应时是一样的。也就是说能量从相消的地方“流”到了相长的地方,从而使得总能量并没有改变。

 微信扫一扫
微信扫一扫 



