答案约是 5000 亿分之一。(一更:撞击到太阳或月球的概率为 10 万分之一,撞击到银河中恒星的概率约为 33 亿分之一。现在知乎竟然还有人看这么枯燥的计算,你们刷小姐姐不好么?)
重要的不是这个结果,而是思考它的过程,还挺有意思的。
1. 直觉
在想这个问题前,我假设你已经了解“晚上的天空为什么会是黑的”这一历史问题了,也就是所谓的“奥伯斯佯谬”。它大致是说,如果宇宙是无限而永恒的,那么星光必然充满宇宙。也就是说,如果宇宙是无限大的,有无数个平均分布的发光星体在其中(且时空平直、没有红移),那么无论望向天上的哪一块位置,都应该见到一粒星体。

开普勒认为,奥伯斯佯谬论证说明宇宙是有限的,或者是只有有限数量的星体。
那么如果开普勒的想法是正确的,这个问题的答案肯定不会是 100%。直觉告诉我们,有可能接近晚上黑夜天空中亮点所占的比例。
下面这张是老当益壮的哈勃十多年前拍的极深场的图像(XDF)。

上面这些密密麻麻的星星,是 5500 个星系[1],每个星系又有无数颗恒星,拥挤在一个 2.3X2 弧分的天空中,相当于整个天空的 32,000,000 分之一的大小[2]。从直觉上来看,题主问题的答案肯定不会是 0%。
2. 如何思考这个问题:假设
首先,我们假设,这个“直线”是一个没有粗细的理想中的几何直线,不像激光笔一样会发散,否则这个问题就失去价值。
其次,我们要假设可观测宇宙的恒星是均匀分布的,并且先忽略太阳甚至银河系的存在,否则它们会干扰我们对整个可观测宇宙的分析。
再次,如果我们接受上面这一个假设的话,那么垂直与否就已经不再重要。对于可观测宇宙来说,我们位于它的中心,并且地球的大小可以忽略不计,所以不论向哪个方向的直线,都是从可观测宇宙的球心发出的,所以是否垂直已经不重要了。
为了计算方便,我们还得假设一个值,那就是恒星的大小。如果均匀分布的每颗恒星都像银河系一样大,那我相信任意直线撞上恒星的概率会大很多很多倍。多年来的观测结果表明,我们附近的大多数恒星都和太阳差不多大,典型直径为 100 万公里左右[3]。因此,我们假设所有恒星的大小都像太阳那么大(太阳的半径取 700000 千米)。
哦,还有一点,我们得定义这里的宇宙是指“现在”的宇宙,而不是我们看到的宇宙。也就是说我们讨论是的是“当下”的 465 亿光年半径的宇宙,而不是哈勃和韦伯看到的那个离大爆炸不久之后的那个宇宙。
3. 如何思考这个问题:立体角
有了上面这些假设,我们才能把问题给简单化,也方便计算。
可是怎么算呢?
最容易想到的方式是,把所有恒星都投影到一个假想的天球上去,看它的投影占整个天球表面积有多少比例。
很多人都会有种错觉,以为星星看上去很大。其实并不是,比如小熊座中那颗很亮的北极星,它是由三颗星组成的,其中北极星 Aa 是太阳的 37.5 倍,距离我们 433 光年左右,可以算出它的“视角”只有约 5 亿分之 1 度[4]。
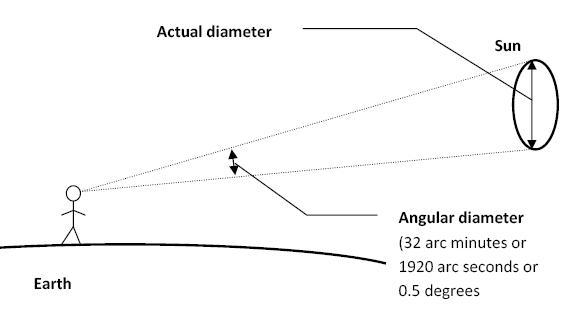
这里的“视角”,指的是星星在我们地球看来的张角,也就是天体中的“角直径”。天空中的 1 度,也就是手臂伸直后小指甲盖那么宽的天空。人眼的极限是 60 分之 1 度,所以没法分辨它(测 E 视力表实际上测的主要就是测这个对视角的分辨能力),只能看到一个亮点。

通过三角函数定义,我们可以知道,那么视角δ就可以写作:

但是视角(角直径)是一个描述“一维”的线的量,我们需要的是天体在天球上的平面投影,是一个二维的面积。
这就用到了一个概念,被称为“立体角”。所谓立体角,在这里和天体的视角“差不多”,就是三维空间中天体对我们的角度,或者说站在某一点的观察者测量到的物体大小的尺度。
当我们看一个恒星球时,视线可以看作是一个立体的圆锥:
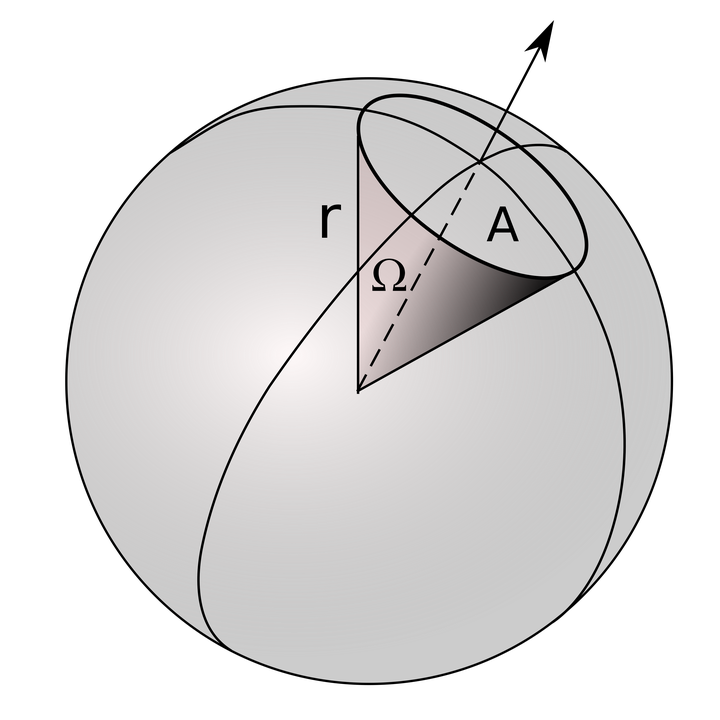
根据公式,可以求得,当到天体的距离 d 远大于天体的半径 R 时,立体角可以写作[5]
太阳是唯一一颗容易测量出立体角的恒星,其它所有恒星都离我们太远,甚至通过最大的地面望远镜,它们看起来也像是一个有着艾里斑的光点。
比如说,100 光年外(也就是约 9X10^14 千米外)的一颗太阳大小的恒星,它的立体角为:
根据定义,还得除以 4\pi,就能得到占到全天球的比例了。这个数值可想而知,太小了。
3.进入正题:洋葱模型
我们可以把宇宙想象成一层球壳包着一层球壳的模样,就像洋葱一样。有点像地心说中亚里士多德的九层天,或者托勒密的 11 层天的那个样子。
为了计算方便,我采用了一位叫 MichaelS 的网友写的代码[6][7]。每一个球壳,我们假设它厚度只有 100 万光年,这相对于 465 亿光年半径的宇宙来说,是比洋葱皮还要薄的一片。在每 100 万光年厚的球壳中,有多少星星呢?
我们现在猜测可观测宇宙中恒星的数量大约为 10 的 24 次方[8],如果假设它们都平均分布的话,全宇宙的平均密度为:
球壳的体积约等于表面积乘上厚度,因此离我们距离为 d 的、也就是半径为 d 的球壳中拥有恒星的数量为
我们把离我们最近的一层球壳称为第 1 层,依次向外是第 2 层、第 3 层....第 k 层...一直到可观宇宙的边缘那一层,也就是第
44000 层。那么 d 就可以表示为
这一层的所有的这些太阳大小的恒星如果不互相遮挡的话,那么它们在在这个球壳上所占有立体角为
简单计算得:
接下来就是简单的求和:
看到这个我真的就不想算了,也不想重新造轮了,直接套用 MichaelS 开发的 C++ 代码,并且考虑到遮挡造成的结果减小,实际算出来就是
再除以 4π的球表面积,也就是说,在我们的一堆假设后,恒星投影看上去只占整个天球的面积 5000 亿分之一。
考虑到银河系的话,撞到的概率会增加一些,毕竟我们看到的星星绝大多数都只是第一层球壳内的银河系邻居。可以把银河系当成平均分布的球状星团洋葱,按 1 光年再切一次。。不行,眼睛有点辣了。。
这样想的话,开光速飞船垂直离开银臂后撞到恒星的概率好低。。。前进四!
“写公式没人看”系列又多了一篇,就先到这儿吧,我打赌也没人认真读到这儿。啦啦啦~~~~~
一更
竟然有人不去看小姐姐和 Jianzheng,还给我提了修改意见,不忘装知乎的初心,好得很。
我就着评论区的几个问题更一下(顺便把上面公式里有一个数写错了给修正了一下,不过估计也没人看):
1.关于太阳和月亮
确实,题主问的是“星球”,那么自然也包括太阳和月亮。
那我们算一下太阳:
这一下子提升了 6 个数量级。嗯,很好。
鉴于月亮和太阳看上去一样大,所以概率是一样的,直接乘 2 。
再除以 4π的球表面积,这样算下来的话,撞击到太阳或月球的概率约为 10 万分之一。
2.关于银河
银河要是一个球状星系的话,也可以直接套上面的洋葱模型。不过真实的银河对我们来说是个扁平的盘子,中心棒结构用同样的模型有点粗糙了。
那么我们就把它中心看成一个棒槌型的洋葱吧。

它里面有恒星的数量级在 10^11 颗,具体多少颗,我们也不知道。就按这个数量级算吧。直径按 10 万光年算,那么我们可以 10 光年切一片,可是它每片的密度。。。。想想有点头大。。。。
具体的我也不算了,还是用 MichaelS 的 C++ 来跑吧,得到的结果我直接抄作业了:
再除以 4π的球表面积,这样算下来的话,撞击到银河中的恒星的概率约为 33 亿分之一。
我写完一摸,午饭都凉了,以后不写这么又臭又长的了。

 微信扫一扫
微信扫一扫 



