题目要求导数是原函数的平移,且平移量为 1。三角函数
就具有这类性质,但平移量为
。指数函数
也具有类似的性质,但平移量为 0。
考虑设计一个指数函数与三角函数相乘的函数,比如
其导数为
原函数平移 1 个单位
两式对比可以得到
问题来了,怎么解这个方程组呢?
第二个式子乘以虚数单位 i,然后两式相加,可以得到
记
,也就是解方程
.
这个方程在复数域内的解与朗伯 W 函数(Lambert W Function) 有关,其解有无数多个,可以表示为
(k 为任意整数)
用 MATLAB 计算的得到的数值解。比如,取 k=0, 此时 a = 0.318131505204764,b = 1.337235701430689.
z = -lambertw(0,-1)
% z = 0.318131505204764 - 1.337235701430689i
画出原函数及其导数的图像
a = real(z);
b = imag(z);
f = @(x) exp(a*x).*sin(b*x);
df = @(x) a*exp(a*x).*sin(b*x) + b*exp(a*x).*cos(b*x);
fplot(f)
hold on
fplot(df)
grid on
legend('f','df')
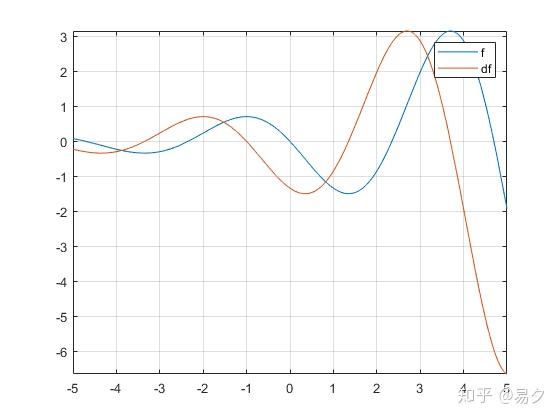
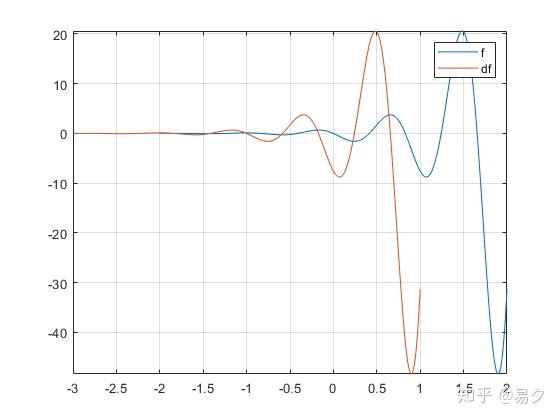
当 k 取其它整数时,也可以得到满足条件的其它函数,比如 k = 1 时,a = 2.062277729598284 ,b = - 7.588631178472513,此时函数图像如下所示

 微信扫一扫
微信扫一扫 



