这个问题非常有意思,高赞答主们从各个角度描述了对数函数的定义及其导数,但是其核心问题还是没有解决,即对数函数
为什么在某些方面像一个幂函数( )。
咋看之下这似乎是无稽之谈,
明明等于
,而其它的幂函数的定义也跟对数函数全然不同,除了对数函数的导数也是幂函数之外,似乎就没有其它相似之处了。
不过非常恰巧,我前段时间对各种不同的平均做了一点点研究,里头也有非常类似的“对数函数表现的像一个幂函数”的行为,不过读者需要先花一点点时间了解一下什么是幂平均。
对于两个正实数
和
,我们知道他们的算术平均是
,几何平均是
,并且有算术几何平均不等式:
,这是中学数学的范畴。
到了大学之后,偶尔我们会遇到另一种平均值:均方根(root mean square, RMS),即
,不过理解这个平均值依然只需要中学数学知识就够了:假设
(下同),不难发现
,所以
确实介于
和
之间,可以当作是某种平均值。
有了均方根,我们很容易就想到,如果把二次方改成三次方行不行?四次方、五次方呢?这就很容易导出了幂平均的概念:
。这样一下子就把算术平均、均方根,推广了无穷多种平均值,只要代入不同的
就可以了,比如调和平均就也被包含了进来:
。
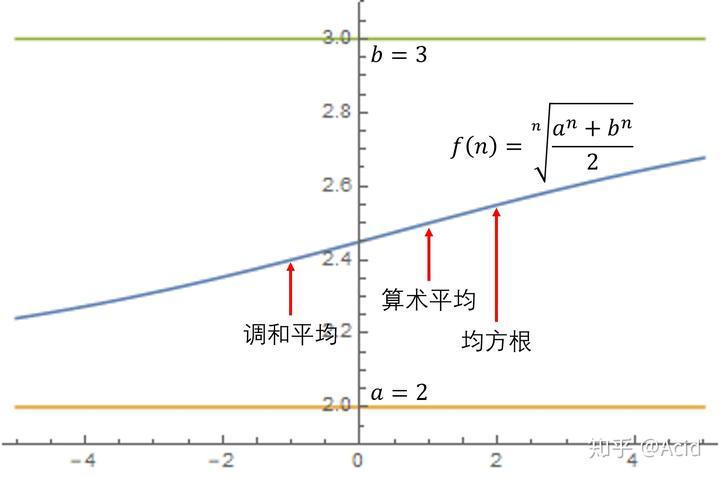
幂平均还有一个很有意思的性质,从图上也可以看出来,就是它关于
是单调的。事实上,如果
趋向于正(负)无穷,那么幂平均就会趋向于
(
)。对于任何有限的
,则幂平均始终在
和
之间。
我们甚至可以对幂平均再做一次推广,把幂函数换成任意函数,把求根换成该函数的逆函数,就得到拟算术平均(quasi-arithmetic mean),又叫广义 f- 平均(generalized f-mean):
,幂平均就对应于
时的情形。
好了,现在背景知识都介绍完了,这与本来的问题有什么关系呢?
别急,我们刚刚忘了提几何平均了,既然幂平均可以一直从
走到
,那几何平均在其中的什么位置呢?
也许你已经猜到了,几何平均就在
的位置!
注意到幂平均在
处是没有定义的,因为不能开零次方根,但是我们可以用极限的角度定义
。
证明其实不难,只要注意到对于任意的
,我们有
,而由于
当
时是单调减的所以不等号要反过来,就可以知道
只能在在
的位置了。
所以按照幂平均与
的对应关系,
似乎对应于
对应的广义平均。然而事实上,
是
下的广义平均。这么一看
是不是跟幂函数
有了某些奇怪的相似关系了?
事实上,幂平均(包含
的特殊情形几何平均)是唯一一种满足齐次性的拟算术平均。什么是齐次性呢?简单地说,
(两米)跟
的平均值,根据平均值的定义方式的不同,不一定是
,也许是比方说
。但是如果我们把这两个数换个单位,那么齐次性要求
跟
在同一个定义下,平均值必须是
。换句话说, 我们要求平均值
满足
,或者更一般的,
,这就是(一次)齐次性。
这个齐次性的要求既自然又苛刻,事实上,只要我们要求广义平均满足齐次性,可以证明
只能是幂函数
或者对数函数
,顶多加上一个常数因子。其它的函数比如指数函数等都是不满足这个性质的。
所以说,对数函数与幂函数的关系远比表面上看起来更加复杂,其中更深入的关系还望有学数学的大神前来揭秘。
竟然这么多人看,趁机推销一下我自己写的段子好了
有哪些学术性强的笑话 / 段子?

 微信扫一扫
微信扫一扫 



