矩阵的本质是什么？(矩阵的本质意义视频)_网络百科

这篇回答节选自我在专栏《机器学习中的数学：线性代数》中的一篇文章，我们从矩阵乘法运算为一个切入点，来谈谈矩阵的本质含义。

欢迎关注我的知乎账号 @石溪，将持续发布机器学习数学基础及算法应用等方面的精彩内容。

1.回顾矩阵的乘法运算

1.1.矩阵的数量乘法

矩阵的数量乘法，描述起来也非常简单：

$c\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix} =\begin{bmatrix} ca_{11} & ca_{12} & ca_{13} \\ ca_{21} & ca_{22} & ca_{23} \end{bmatrix}$

同样，我们看一个代码的例子：

代码片段：

import numpy as np
A = np.array([[1, 2, 3],
              [4, 5, 6]])
print(2*A)

运行结果：

[[ 2  4  6]
 [ 8 10 12]]

1.2.矩阵与矩阵的乘法

矩阵与矩阵的相乘，过程要稍微复杂一点，因此我们拿出来单讲。例如下面举例的矩阵

$A$

和矩阵

$B$

的乘法运算，对两个矩阵的形态是有要求的。

$\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{bmatrix} ×\begin{bmatrix} b_{11}&b_{12}&b_{13} \\ b_{21} &b_{22}&b_{23} \end{bmatrix} =\begin{bmatrix} a_{11}b_{11} +a_{12}b_{21}&a_{11}b_{12} +a_{12}b_{22}&a_{11}b_{13} +a_{12}b_{23} \\ a_{21}b_{11} + a_{22} b_{21}& a_{21}b_{12} + a_{22} b_{22}& a_{21}b_{13} + a_{22} b_{23}\\ a_{31}b_{11} + a_{32} b_{21}&a_{31}b_{12} + a_{32} b_{22}&a_{31}b_{13} + a_{32} b_{23} \end{bmatrix}$

仔细观察这个计算公式，我们总结出以下的一些要求和规律：

1 左边矩阵的列数要和右边矩阵的行数相等

2 左边矩阵的行数决定了结果矩阵的行数

3 右边矩阵的列数决定了结果矩阵的列数

同样，我们用

$python$

来演示下面这个例子：

$\begin{bmatrix} 1 & 2 \\ 3 &4 \\ 5& 6 \end{bmatrix} × \begin{bmatrix} 3&4&5 \\ 6 &7&8 \end{bmatrix}$

代码片段：

import numpy as np

A = np.array([[1, 2],
              [3, 4],
              [5, 6]])
B = np.array([[3, 4, 5],
              [6, 7, 8]])

print(np.dot(A, B))

运行结果：

[[15 18 21]
 [33 40 47]
 [51 62 73]]

2.改变空间位置：矩阵乘以向量的本质

矩阵与向量的乘法，一般而言写作矩阵

$A$

在左，列向量

$x$

在右的

$Ax$

的形式。这种

$Ax$

的写法便于描述向量

$x$

的位置在矩阵

$A$

的作用下进行变换的过程（下面会详细介绍）。

矩阵与向量的乘法，其实可以看作是矩阵与矩阵乘法的一种特殊形式，只不过位于后面的矩阵列数为 1 而已。

$\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{bmatrix} \begin{bmatrix} x_{11} \\ x_{21} \end{bmatrix} =\begin{bmatrix} a_{11}x_{11} +a_{12}x_{21} \\ a_{21}x_{11} + a_{22} x_{21}\\ a_{31}x_{11} + a_{32} x_{21} \end{bmatrix}$

我们对照前面讲过的矩阵与矩阵的乘法，来对比一下矩阵与向量的乘法规则，我们把列向量看作是列数为 1 的特殊矩阵，那么就会非常明确：

1、矩阵在左，列向量在右，矩阵的列数和列向量的维数必须相等

2、矩阵和向量相乘的结果也是一个向量

3、矩阵的行数就是最终结果输出的列向量的维数

4、乘法的规则如上所示，就是矩阵的每行和列向量进行对应元素分别相乘后相加

我们来看一个矩阵与列向量相乘的例子：

$\begin{bmatrix} 1 & 2 \\ 3 &4 \\ 5 &6 \end{bmatrix} \begin{bmatrix} 4 \\ 5 \end{bmatrix} =\begin{bmatrix} 1×4 +2×5 \\ 3×4 + 4× 5\\ 5×4 +6×5 \end{bmatrix} = \begin{bmatrix} 14 \\ 32\\50 \end{bmatrix}$

代码片段：

import numpy as np
A = np.array([[1, 2],
              [3, 4],
              [5, 6]])
x = np.array([[4, 5]]).T

print(np.dot(A, x))

运行结果：

[[14]
 [32]
 [50]]

从结果看，原始向量表示二维空间中的一个点，坐标为

$(4,5)$

，经过矩阵

$\begin{bmatrix} 1 & 2 \\ 3 &4 \\ 5 &6 \end{bmatrix}$

乘法的作用，转化为三维空间中坐标为

$(14,32,50)$

的点。

因此从这个例子中我们可以总结一下矩阵的作用：在特定矩阵的乘法作用下，原空间中的向量坐标，被映射到了目标空间中的新坐标，向量的空间位置（甚至是所在空间维数）由此发生了转化。

关注 @石溪知乎账号，分享更多机器学习数学基础精彩内容。

3.从行的角度思考

学习了矩阵、向量的表示方法以及运算规则之后，我们回过头来静静的思考一个问题：矩阵

$A$

和列向量

$x$

的乘法

$Ax$

到底意味着什么？下面，我们就来挖掘一下这里面的内涵。

在二阶方阵

$A$

与二维列向量

$x$

相乘的例子中，

$Ax=\begin{bmatrix} a & b \\ c &d \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}=\begin{bmatrix} ax_1 +bx_2 \\ cx_1+dx_2 \end{bmatrix}$

。

刚才说了，位于矩阵

$A$

第

$i$

行的行向量的各成分和列向量

$x$

各成分分别相乘后相加，得到的就是结果向量的第

$i$

个成分。这个计算方法有没有感觉很熟悉？没错，这不就是向量点乘的定义式么？

即：

$Ax=\begin{bmatrix} row_1 \\ row_2 \end{bmatrix} x=\begin{bmatrix} row_1 \cdot x\\ row_2 \cdot x\end{bmatrix}$

]。

矩阵与向量的乘法如果从行的角度来看，就是如此。常规的计算操作就是这么执行的，但是似乎也没有更多可以挖掘的，那我们试试继续从列的角度再来看看。

4.列的角度：重新组合矩阵的列向量

如果从列的角度来计算矩阵与向量的乘积，会有另一套计算的方法，可能大家对这种方法要相对陌生一些。但是实质上，这种方法从线性代数的角度来看，还要更为重要一些，我们还是用二阶方阵进行举例。

$Ax=\begin{bmatrix} a & b \\ c &d \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}=x_1\begin{bmatrix} a\\ c\end{bmatrix} +x_2\begin{bmatrix} b\\ d\end{bmatrix}=\begin{bmatrix} ax_1 +bx_2 \\ cx_1+dx_2 \end{bmatrix}$

发现了规律没有？我们通过这种形式的拆解，也能得到最终的正确结果，这就是从列的角度进行的分析。从前面的知识我们可以这样描述：从列的角度来看，矩阵

$A$

与向量

$x$

的乘法是对矩阵

$A$

的各列向量进行线性组合的过程，每个列向量的组合系数就是向量

$x$

的各对应成分。

这么理解似乎有点新意，我们按照列的思想重新把矩阵

$A$

写成一组列向量的形式：

$Ax=\begin{bmatrix}col_1 & col_2 &...&col_n\end{bmatrix} \begin{bmatrix}x_1\\x_2\\...\\x_n\end{bmatrix}=x_1col_1+x_2col_2+...+x_ncol_n$

依照上述公式，我们举一个实际的例子，就更清楚了。

$Ax=\begin{bmatrix} 1 & 2 \\ 3 &4 \end{bmatrix} \begin{bmatrix} 3 \\ 5 \end{bmatrix}=3\begin{bmatrix} 1\\ 3\end{bmatrix} +5\begin{bmatrix} 2\\ 4\end{bmatrix}$

所得到的结果就是矩阵第一列的列向量

$\begin{bmatrix} 1\\ 3\end{bmatrix}$

的 3 倍加上第二列列向量

$\begin{bmatrix} 2\\ 4\end{bmatrix}$

的 5 倍。

因此，一个矩阵和一个向量相乘的过程，就是对位于原矩阵各列的列向量重新进行线性组合的过程，而线性组合的各系数就是向量的对应各成分。

5.进一步引申：变换向量的基底

5.1.二阶方阵与二维列向量乘法举例

为了方便说明原理，我们依旧用二阶方阵

$\begin{bmatrix} a & b \\ c &d \end{bmatrix}$

与二维列向量

$\begin{bmatrix} x \\ y \end{bmatrix}$

的乘法进行举例：

二维列向量

$\begin{bmatrix} x \\ y \end{bmatrix}$

的坐标是

$x$

和

$y$

，还记得之前我们介绍过的向量坐标的概念么？向量的坐标依托于基底的选取，向量坐标在基底明确的前提下才有实际意义，而这个二维列向量，我们说他的坐标是

$x$

和

$y$

，基于的就是默认基底：(

$\begin{bmatrix} 1 \\0 \end{bmatrix}$

和

$\begin{bmatrix} 0 \\1 \end{bmatrix})$

。那么二维列向量的完整表达式就是：

$\begin{bmatrix} x \\y\end{bmatrix}=x\begin{bmatrix} 1 \\0 \end{bmatrix} +y\begin{bmatrix} 0 \\1 \end{bmatrix}$

。

好，回顾了这些基础，我们就利用他将矩阵与向量的乘法表达式做进一步的展开：

$\begin{bmatrix} a & b \\ c &d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}[acbd][xy] =\begin{bmatrix} a & b \\ c &d \end{bmatrix} (x\begin{bmatrix} 1 \\ 0 \end{bmatrix} +y\begin{bmatrix} 0 \\ 1 \end{bmatrix}) =x\begin{bmatrix} a & b \\ c &d \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} +y\begin{bmatrix} a & b \\ c &d \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix}=x\begin{bmatrix} a \\ c \end{bmatrix} +y\begin{bmatrix} b \\ d \end{bmatrix}$

是不是已经初见端倪了？我们再直观的展示一下式子首尾的结果，在矩阵

$\begin{bmatrix} a & b \\ c &d \end{bmatrix}$

的乘法作用下，向量完成了下面的转换：

$x\begin{bmatrix} 1 \\ 0 \end{bmatrix} +y\begin{bmatrix} 0 \\ 1 \end{bmatrix}\Rightarrow x\begin{bmatrix} a \\ c \end{bmatrix} +y\begin{bmatrix} b \\ d \end{bmatrix}$

挑明了说，就是矩阵把向量的基底进行了变换，把旧的基底 (

$\begin{bmatrix} 1 \\ 0 \end{bmatrix}$

$\begin{bmatrix} 0 \\ 1 \end{bmatrix}$

)变换成了新的基底(

$\begin{bmatrix} a \\ c \end{bmatrix}$

$\begin{bmatrix} b \\ d \end{bmatrix}$

)。

映射前由旧的基底分别乘以对应的坐标

$(x,y)$

来表示其位置，而映射后，由于旧的基底映射到新的基底，那向量自然而然应该用新的基底来分别乘以对应坐标

$(x,y)$

来描述改变后的空间位置，

$x\begin{bmatrix} 1 \\ 0 \end{bmatrix} +y\begin{bmatrix} 0 \\ 1 \end{bmatrix}\Rightarrow x\begin{bmatrix} a \\ c \end{bmatrix} +y\begin{bmatrix} b \\ d \end{bmatrix}=\begin{bmatrix} ax +by \\ cx+dy \end{bmatrix}$

，如图 1 所示。

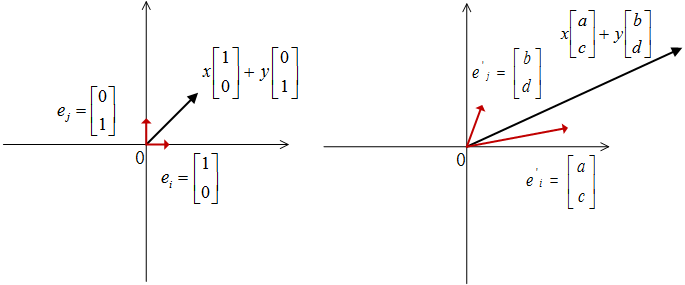
5.2.矩阵的各列就是映射后的新基底

结合矩阵的式子我们不难发现：矩阵

$A$

的第一列

$\begin{bmatrix}a \\ c \end{bmatrix}$

就是原始的默认基向量

$\begin{bmatrix} 1 \\ 0 \end{bmatrix}$

变换后的目标位置（新的基向量），而第二列

$\begin{bmatrix} b \\ d \end{bmatrix}$

就是另一个基向量

$\begin{bmatrix} 0 \\ 1 \end{bmatrix}$

映射后的目标位置（新的基向量）。

基底的变换明确了，那向量的坐标呢？映射后得到的新向量，如果以 (

$\begin{bmatrix} a \\ c \end{bmatrix}$

$\begin{bmatrix} b \\ d \end{bmatrix}$

)为基底，他的坐标仍是

$(x,y)$

，如果以默认的(

$\begin{bmatrix} 1 \\ 0 \end{bmatrix}$

$\begin{bmatrix} 0 \\ 1 \end{bmatrix}$

)为基底，那么其坐标就是

$(ax +by,cx+dy)$

。

5.3.扩展到三阶方阵

为了让结果更让人信服，我们再看看三阶方阵和三维列向量相乘的例子，同理也满足这个过程：

$\begin{bmatrix} a & b& c\\ d & e& f\\ g & h&i \end{bmatrix} \begin{bmatrix} x \\ y\\ z \end{bmatrix} =\begin{bmatrix} a & b& c\\ d & e& f\\ g & h&i \end{bmatrix} (x\begin{bmatrix} 1 \\ 0\\ 0 \end{bmatrix} +y\begin{bmatrix} 0 \\ 1\\ 0 \end{bmatrix}+z\begin{bmatrix} 0 \\ 0\\ 1 \end{bmatrix})= x\begin{bmatrix} a \\ d\\ g \end{bmatrix} +y\begin{bmatrix} b \\ e\\ h \end{bmatrix}+z\begin{bmatrix} c \\ f\\ c \end{bmatrix}$

是不是和二阶矩阵的情况是一模一样呢？三阶方阵将三维列向量的基底做了映射转换，方阵的第一列

$\begin{bmatrix} a \\ d\\ g \end{bmatrix}$

是原始基向量

$\begin{bmatrix} 1 \\ 0\\ 0 \end{bmatrix}$

映射后的目标位置（新的基向量），方阵的第二列

$\begin{bmatrix} b \\ e\\ h \end{bmatrix}$

是原始基向量

$\begin{bmatrix} 0 \\ 1\\ 0 \end{bmatrix}$

映射后的目标位置（新的基向量），方阵的第三列

$\begin{bmatrix} c \\ f\\ i \end{bmatrix}$

是原始基向量

$\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}$

映射后的目标位置（新的基向量）。

因此同样的，映射后的目标向量如果在新的基底

$(\begin{bmatrix} a \\ d\\ g \end{bmatrix} ,\begin{bmatrix} b \\ e\\ h \end{bmatrix},\begin{bmatrix} c \\ f\\ c \end{bmatrix})$

下看，其坐标仍然是

$(x,y,z)$

。如果放回到原始基底

$(\begin{bmatrix} 1 \\ 0\\ 0 \end{bmatrix} ,\begin{bmatrix} 0 \\ 1\\ 0 \end{bmatrix},\begin{bmatrix} 0 \\ 0\\ 1 \end{bmatrix})$

下看，将新的基底

$(\begin{bmatrix} a \\ d\\ g \end{bmatrix} ,\begin{bmatrix} b \\ e\\ h \end{bmatrix},\begin{bmatrix} c \\ f\\ c \end{bmatrix})$

和他对应的坐标

$(x,y,z)$

相结合，就能得到默认原始基底下的坐标：

$\begin{bmatrix} ax+by+cz \\ dx+ey+fz\\ gx+hy+iz \end{bmatrix}$

。

5.4.一般化的： $m×n$ 矩阵乘以 $n$ 维列向量

此处，我们看到的就是最一般的情况了，矩阵

$A=\begin{bmatrix} a_{11}&a_{12}&...&a_{1n} \\ a_{21}&a_{22}&...&a_{2n}\\ ...&...&...&...\\ a_{m1}&a_{m2}&...&a_{mn} \end{bmatrix}$

和向量

$x= \begin{bmatrix} x_1 \\ x_2\\ ...\\ x_n \end{bmatrix}$

进行相乘。

$Ax = \begin{bmatrix} a_{11}&a_{12}&...&a_{1n} \\ a_{21}&a_{22}&...&a_{2n}\\ ...&&...\\ a_{m1}&a_{m2}&...&a_{mn} \end{bmatrix}\begin{bmatrix} x_1 \\ x_2\\ ...\\ x_n \end{bmatrix}=x_1 \begin{bmatrix} a_{11} \\ a_{21}\\ ...\\ a_{m1} \end{bmatrix}+x_2 \begin{bmatrix} a_{12} \\ a_{22}\\ ...\\ a_{m2} \end{bmatrix}+...+x_n \begin{bmatrix} a_{1n} \\ a_{2n}\\ ...\\ a_{mn} \end{bmatrix}$