这个问题很老套，但是我所看到的回答其实没有令人满意的，这里面误解重重，即使是一些专业人士也不能免俗。

it must be said that in the grand contest for the most misunderstood idea in the history of physics, entropy is probably the winner.（如果举行一个物理学史上被误解概念的大赛的话，熵大概就是冠军） - Jeremy England

这里我试着从三个方面来阐释这个问题（一般最常见的回答只是指出了第一个方面而已）：

1. 进化论不违背熵增原理
2. 全局熵增下的局部熵减是完全可能的且常见的
3. 进化论不但不违背熵增，反而是是熵增原理的自然结果。

本回答各处均浅尝辄止，算是给我的第三个专栏整理一下思路吧。后面有些参考文献可供大家进一步阅读。

1、什么是熵增原理？

熵增原理是热力学第二定律的一种表述形式。一般而言，大家所提及的熵增原理说的是，在一个孤立系统中熵总是不减的。请注意这里的两个重点，“孤立系统”和“不减”。

孤立系统指的是一个和环境既没有质量交换也没有能量交换的系统。很显然地球并不是一个孤立系统。因而地球的熵并不一定会单调增加。这是对本问题的最直接回答。

但是这个回答中，只是说了熵增和进化论不矛盾，并没有说它们之间存在的关系。如果我们进一步，就需要考虑封闭系统和开放系统的问题了。

2、熵增原理仅适用于孤立系统吗？

很明确，熵增原理并不仅限于孤立系统。事实上，在封闭系统中它可以被克劳修斯不等式来表述：

简言之，就是在一个封闭系统中，熵变去掉过程中热温商的路径积分后总是大于零。在这里这个 N，被克劳修斯称作“uncompensirte Verwandlung （无补偿变化）”。所以克劳修斯的另外一个热力学第二定律表述就是：

无补偿变化总是为正数^[1]。

克劳修斯并没有能够给出这个 N 的数学描述。我猜他肯定是想这么做，但是限于当时的理论水平，做不到。因为这个 N 涉及到了对具体的不可逆过程的数学描述。而经典热力学一直到 1930 年代都还仅限于平衡态热力学。

不论如何，如果一个过程中热温商的路径积分是负数，那么系统显然是有可能向着熵减的方向变化的。也就是说，熵增原理不禁止封闭系统的熵减（地球可以近似看作是一个封闭系统），因而就有可能与进化论不发生冲突。

3、熵增原理更加普遍的表述

在现代热力学中，人们一般把克劳修斯的“无补偿变化”，这个 N，叫做熵产生（entropy production），指的是系统内部自发的不可逆过程导致的熵增。因而，对一般的封闭系统而言，克劳修斯不等式其实就是在说，系统的熵产总是为正数。

请注意，这个表述并不仅限于孤立系统。

有很多人（包括一些专业人士）在反驳“进化论违背熵增”这个问题的时候，往往会犯很多错误。第一个错误就是，他们会说熵增原理仅适用于孤立系统，有人甚至说热力学第二定律仅适用于孤立系统，这是大错特错的。熵增原理不但可以应用在封闭系统，而且可以用在开放系统。事实上在能源领域，最常见的诸如电厂，热力学的应用基本上都是针对开放系统的。比如说在开放系统中：

用人话来说，就是：

系统的熵变=进出系统的净熵 + 进出系统的经热流引发的熵变 + 系统内部的熵产生

也就是说，在一个开放系统中，系统的熵变由三个因素决定：

1. 进出系统的熵流
2. 进出系统的热流
3. 系统内部的演化所导致的熵产生

在上述三个因素中，热力学第二定律断定，第三个总为正，而其他两个则取决于边界条件，例如是净流入还是净流出。所以，在开放系统中，系统的熵变去掉净熵流和净热流的贡献后，总是为正数。

也就是说，即使是在地球这样的开放系统中，下面这个更加普遍的熵增原理是成立的：

一个系统的熵产生总是正数。

4、一般而言系统并不向着熵最大的方向演化

所以，我们可以看到，在一个一般系统中，我们所谓的熵增，其实是说的是熵产生总是净正值，但是并不必然是系统的熵值总是增大 - 因为随着系统与环境的物质和能量交换，它同时与环境交换着熵。前面所说，简言之就是：

熵产生=系统的熵变 - 系统与环境的熵交换≥0

因此随着边界条件的变化，系统最终的稳定存在并不一定是熵最大的平衡态。比如说，我们拿一根温度为

的铁棒，一端连接一个

的热源，另一端连接一个

的冷源。很显然，最终铁棒收敛的状态就是一个内部有着温度线性分布的状态。我们可以计算这个过程中铁棒的熵变，很容易得到：

其中：

很显然对于铁棒而言这是一个熵减过程。当然我们也可以计算，整个过程中铁棒的熵产生总是大于零的。

也就是说，在这个例子中，在两端冷热源的边界条件限制下，系统演化的最终状态并不是一个熵最大的状态。

事实上，在系统外部存在不均一的边界条件，以至于系统内部存在着能量流动的情况下，局部的熵减是完全可能的甚至是必需的。有时候它甚至会有剧烈的熵减过程。

我们用一个流水的例子做一个类比。在简单的“流水”系统中，熵增原理的等效说法就是系统的势能总是趋向于最小化，用大白话说就是“水往低处流”。现在我们有一个地下暗渠，连通着山顶的一个湖泊和山底下的一条河流。暗渠与地面有一条裂隙联通，如下图所示

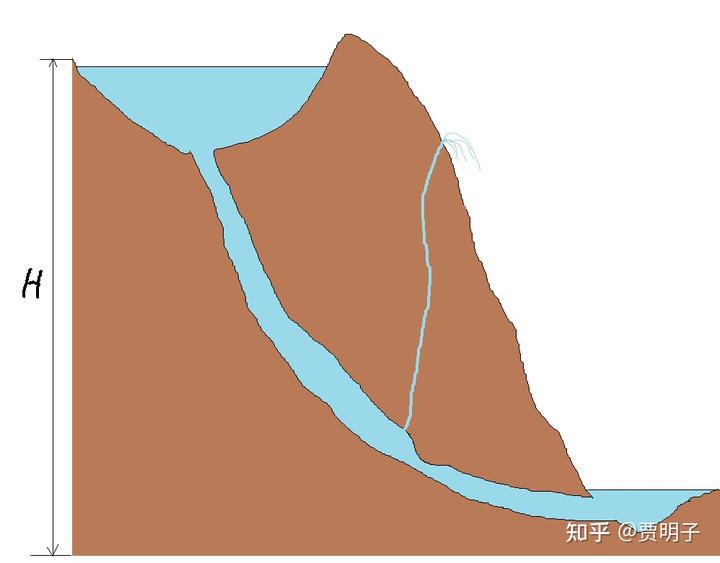
水会顺着暗渠向下流动。我们假定湖泊和河流的体积巨大，因此这里我们可以固定它两端边界条件，一端高度为 H，另一端为零。

但是，如果暗渠突然发生了栓塞。这个栓塞是瞬时发生的，比如说一块石头顺流而下突然堵死了一处喉管。这个时候，水流就会突然被停止，瞬间的动能停止就会被转化为巨大的静压（这个叫做水锤效应）。这个压力非常之大，远远超出了 H 的高度。于是它会从裂隙中喷出，形成高高的喷泉。（原谅我的灵魂画技）

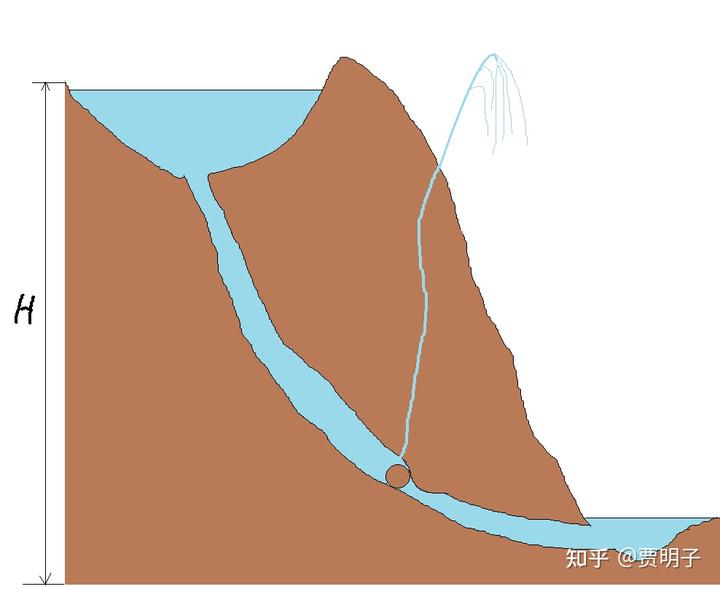
这股喷泉完全可能高于湖泊的最高处。但是他只是一个脉冲，等它喷出后，暗渠内的压力被泄掉，喷泉就消失了。

在这个例子里，由于内部的能量流动，在某个局部可能会产生比原来最高处还要高的喷泉。当然整个系统却并不违背“水往低处流”的基本原理。因为这股喷泉是以大量水体的动能消失为代价的。原来这些流水由于本身的动能，仍然存在爬升一定高度的潜力，但是现在这种潜力都消失了，换来了一小股水爬升到更高的高度。

这股例子想说明的是，在不均一的外部边界条件下，系统内部的稳态不但不是熵最大的状态，而且完全可以自发产生局部的巨大熵减过程。

另外，水往低处流的过程，并非简单地流下去的，而是会形成很复杂的分支，就像是这样：

这种分支是一种分形结构。它有着极高的规则性。也就是说，这是一种整体熵增过程中自然形成的，极其规则的结构。事实上，这种分支结构不是没有原因的：它的形成导致了水流动过程中的阻力最小（这在我们后面会提到），因而会使得水流更多（也就是整体的熵增更快）。也就是说，这种局部规则结构的形成，其后果恰恰是使得熵增的速度最大化。

5、势、力、流

上面说了大家常犯的第一个错误，就是误以为熵增原理仅适用于孤立系统。那么，大家容易犯的第二个错误是什么呢？这个错误就是，很多人会说热力学仅适用于平衡系统。这个显然也是大错特错的。事实上非平衡态热力学现在早已经发展了大半个世纪了。

事实上，早在 1930 年代，关于非平衡态热力学的研究就开始了。

因为非平衡态中各项性质不再是均匀分布，在系统中就会有各种梯度和流动。这些梯度对应着不同的“势”，由于梯度的存在就相应地产生驱动力，这种“力”就会产生“流”。做一个类比，就是重力势能的梯度就是重力，而重力就成为水往低处流的“流”的驱动力。这些热力学的“力”和“流”就有类似的对应关系。例如，温度梯度就成为能量从高温向低温流动的驱动力（热流），浓度梯度就成为质量从高浓度向低浓度流动的驱动力（质量流），化学势（或者是化学亲和力，Affinity）就成为原子从反应物向产物流动的驱动力（化学反应流），如此等等。

非平衡态热力学中，就研究热力学力和热力学流之间的关系以及因此产生的状态函数的变化。

那么，对于一个非平衡态的开放系统，它的熵变就是这样的：

其中

就是熵产生。我们可以得到，熵产生满足如下关系：

其中

为热力学力，

为热力学流。^[2]

当系统临近平衡态的时候，力相对较小，流也不显著，这时候可以近似地用线性关系来表示它们之间的关系：

其中

这就是线性非平衡态热力学的最基本公式和昂萨格倒易关系^[3]。

6、更加普遍的熵增原理：最大熵产生原理（Maximum Entropy Production Principle MEPP）

随着大家对非平衡态的研究，1945 年普利高津提出了线性区的最小熵产生原理^[1]（MinEp）。随后 Ziegler 在 1983 年提出了最大熵产生原理（MaxEp 或 MEP）^[4]。（请注意这两个原理并不矛盾，事实上前者可以看做是后者的一个特例^[5]）。这个原理这样说：

If irreversible force is prescribed, the actual flux ..., maximizes the entropy production.（给定热力学力，那么它所驱动的流……将使得熵产生最大化）

虽说是这个原理是以热力学第二定律为前提导出的，但是反过来如果我们预先假定这个原理，热力学第二定律就可以看做是最大熵产生原理的推论。直观上来讲，经典的热力学第二定律说熵是净产生的（熵产生>0），这个原理进一步说，熵不但是净产生的，而且是以边界条件限定下向着最快速度产生的方向演化。应用于孤立系统，经典熵增原理说系统总是向着熵最大的平衡态演化，而这个原理说，熵沿着通向平衡态的最快路径演化。这就有些最小作用量原理的意思了。文献中，尤其是近年来，有很多关于这个原理和最小作用量原理的关系的研究^[6]。

事实上，Ziegler 并不是最早提出这个原理的人。早在 100 年前玻尔兹曼就提出过这样的猜想。从熵的统计诠释来看，这种猜想是比较合理的：既然熵最大的状态是最可能存在的状态，那么在任何时刻，系统向着该状态的演化总是有着压倒性的概率的。1954 年 Zimen 正式提出过这个原理，但是是 Ziegler 用最严谨的方式证明的，因此它又叫 Ziegler 原理。

熵产生最大原理形成的时间比较晚，并且知名度远远不及它的同胞兄弟熵产生最小原理（这可能是普大叔的极力科普的结果，但是从数学上看，它的普适度远远超过了熵产生最小原理）。因此现在学界对它的正确性、适用范围仍有争议。但是它在全球气候、生态圈、生物进化等各个领域有着越来越广泛的应用。如果我们假定这是个普适的定律，那么我们就获得了熵增原理的最普遍表述形式：

对某个固定边界条件下的任意系统，系统的状态使得熵产生最大。

对于 MEP，有不同的物理学家、化学家在不同时期提出，但是它们的含义都略有不同，并且适用的边界条件也有所变化。根据不同科学家的语境^[7]，它可能是：

1. 一个系统的局部熵产生最大（请注意这里局部熵产生最大和全局熵产最大生并不一定一致。熟悉优化原理的人大概都知道，一个局部的最速下降算法，在全局而言不一定是最速的，但是它一定是向着最速下降方向的）。但是进化系统本身足够复杂，各种方向的随机变化都有足够的概率，因此各种不同的可能路径都在不同的子空间“试探”，在不同的局部结构中，就会有不同的最速下降方向，因此就会演进出不同的“路线”：这可能就是生物进化树不断分支的原因。
2. 一个固定边界条件下多重稳态结构里，系统选择熵产生最大的稳态。这一点不论是理论还是实验，都有着证明^[8]。但是似乎并不适合本问题，因为进化过程显然并不是稳态。
3. 统计力学意义上的最可几路径。
4. 固定热力学力边界条件下系统的能量耗散速率最大。

对于这些略有差异的不同原理，其实用在生态圈和生命进化领域，最终结果也都略有不同。本文篇幅有限不做细节讨论。下面只是简单说明，在生物进化过程中伴随着的，是地球生态圈的熵产生速率不断增加，这显然是和热力学第二定律相符的。

7、"生命即化学“

生命的产生和进化过程，可以看做是一种复杂的化学网络。在最初的“原汤”中，存在着各种各样的物质，它们之间有着非常复杂的化学反应。当然这是一个开放系统。所有这些化学反应最终会导向自由能最低的状态（等效于熵产生大于零的状态）。按照熵产生最大原理，这些化学反应的路径必然使得这种能量耗散最快。

我们用一个简单的例子来做一个类比：最简单的酸碱中和反应。

我们知道，酸碱反应就是

和

之间的反应。而这两种离子的出现需要水。比如说我们把固体的柠檬酸和苛性钠混合到一起，从化学平衡的角度，我们知道下述反应基本上就是不可逆的：

但是这个反应本质上是氢离子和氢氧根离子之间的反应：

也就是说，在没有水的存在时，不存在各种离子，也就不会发生化学反应。如果我们把柠檬酸和 NaOH 混合在一起，并且放置在一个完全干燥的环境下，我们看不到这个反应会发生。哪怕这个反应会极大地降低系统的自由能。

只有在有液态水的情况下，这种反应才可以进行下去。这里的特殊之处在于，水同时是这个反应的产物。一旦启动了这个化学反应，就有水生成。有水生成，就会使得化学反应发生。进而产生更多的水。而更多的水就会引发更多的酸碱反应。也就是说，整个系统就会加速向着酸碱中和的方向进行。最终使得整个酸碱中和反应彻底完成，从而导致自由能的快速耗散 - 也就是宇宙的“快速”熵增。

我们可以看到，在这个过程中，水的作用极其关键。它有两个特征：

1. 加快反应速度，也就是加速熵产生
2. 自产生：也就是说，它的“后裔”是自己加速反应后的产物。

由于这两个特征的存在，使得柠檬酸 +NAOH 的体系中几乎是必然会产生水，并且越来越多。这是热力学第二定律的直接结果。

而生物恰恰有两个非常相似的特征：

1. 生物的代谢、繁衍过程加速熵产生
2. 生物可以自我复制：它的后裔是自己消耗大量资源，加速了熵产生后的产物。

相类似地，在热力学第二定律的作用下，生命的产生不但不奇怪，而且是非常顺理成章的。

8、生命是什么

1953 年，克里克在发现了 DNA 双螺旋结构以后，把他和沃森划时代的论文寄给了薛定谔，并且写道：

亲爱的薛定谔教授：
有一次沃森和我谈起我们为何进入分子生物学这个领域，我们发现我们都是受了您的一本小册子《生命是什么》的影响。
我觉得您可能会对随信寄出的论文感兴趣 - 您会看到，您所谈到的“准周期晶体”似乎是（对 DNA 分子的）一个非常贴切的名称。
您真诚的，
F. H. C. 克里克

克里克这里说的，就是薛定谔著名的《生命是什么？》^[9]薛定谔虽然不是生物学家，但是这本书在生物界却引起了极大的震动。

前面我说了大家的两个常见误解。这里说第三个。在知乎上有一种似乎是政治正确的说法，认为这本书不过是薛定谔跨界的指手画脚，只有含糊不清的猜想和似是而非的哲学思辨，而没有专业价值。事实上从 google scholar 上我们可以看到，这本著作在专业圈子里被引用次数极多，与其它一般学术著作相比是压倒性的。在这本书里面除了关于 DNA 结构的猜想，更加引人注目的一个观点，就是生命以负熵为食：它从外界猎取低熵能量，然后向外界排除高熵的热量，从而在与外界的熵交换过程中获得大量的熵的净流出。从而在自身熵产生不断累积的情况下，保证了自身的低熵态，也就是有序的生命结构。

一个成年的生命，比如说，一个成年人类，在维持自己生命的过程中，自身的熵值大致上是不太变化的，因为我们的身体结构并不会有太多变化。那么，从热力学的基本公式中看：

由于自身的熵产生永远大于零，那么必然自身的净熵流为负数。从这个意义上，生命以负熵为食无疑是正确的。

这个观点无数人耳熟能详。这里我不想过度展开。只是想说，这个观点有两个重大意义

1. 开启了热力学角度思考进化的先河。这方面的研究，大概仅仅是在最近的二三十年才渐渐繁荣起来；
2. 指出了，生命的低熵结构与热力学定律之间的自洽性。

9、进化和熵增

我们回到前面“生命即化学”的相关讨论。我们说到，生命的存在加速熵产生速率，并且生命有自我复制的能力。这使得生命像极了一种自催化系统。它产生自反应系统本身，并且不断复制，同时加速了反应速度，也就是系统熵产生的速度。

事实上，如果我们考虑地球这个开放系统，它有着两个固定边界条件：第一，就是太阳 6000℃的辐射作为热源，第二就是背向太阳低温的冷源。这就像前面的例子是一样的。在地球上这样的系统中，我们考虑它的熵产生，它是最大的。

毫无疑问，生命在维持自身生命过程的时候，必须要不断地猎取能量，并且向外排出废热的。这使得生命代谢过程本身就是在加速熵产生。那么生命在成长和复制的过程呢？这个过程中也是在产生净熵增的。Jeremy L. England^[10]曾经用统计力学估算了细胞的复制过程中对能量的耗散下限：

无论是生命的代谢、成长、还是繁衍，都是会产生能量的净耗散的。也就是说，所有的生命活动都是在加速系统的熵产生的。从这个角度上讲，生命不但不违背热力学第二定律，反而是热力学第二定律的必然结果。

我们可以举个例子。比如说一颗小树。当它生成第一片树叶的时候，这片树叶从环境中猎取太阳光的辐射能量，然后向外排出废热。这个过程加速了熵的净增长之外，也加速了自身的生长。于是就产生了第二片树叶。第二片树叶就更加快环境的熵增，同时加速自己的第三片树叶……，这是一种正反馈过程。

那么，整个进化过程呢？

在一个有限资源的环境中，物种之间的竞争结果，就是那些能够猎取更多能量的物种生存下来。请记住，生物就是一个把能量耗散掉从而产生净熵增的一个自催化系统。那么这些猎取更多能量的物种自然就会产生更多的净熵增。

比如说，增加自己生存能力的一个手段就是更加有效地增殖。就像我们前面说的，增殖过程就是一个加速熵增的过程。因而当生物进化到更加有效地增殖的时候，系统就变得熵产生更高。

再比方说，增加自己的速度也是一个有效的生存能力。显然增加速度必须是以更多地耗散能量为代价的。

当生物向着更加适应环境的方向进化的时候，其实是在向着“增加能量耗散”的方向进化。也就是说，各种物种在这种过程中，热力学第二定律假生命之手，加速了整个系统的熵增。

10、热力学第二定律“喜欢”生命

我们可以想象一个极端的情况，做一个极其简化的计算。假设两个地球的复本 A 和 B。A 上面没有生命，B 上面被绿叶植物完全覆盖。那么会发生什么呢？

在 A 地球中，日间太阳的辐射照射在地表，有一部分被反射，另一部分被吸收。那么地球的温度相应上升。那么从太阳进入地球的熵流就正比于太阳常数。到了夜间，地表热量以低温的形式辐射到太空。一个昼夜循环，我们简化起见，假设温度回归。也就是说，日间吸收的热量全部以高熵态返还给太空。一进一出之后，整个系统的熵增是：

其中

是吸收的太阳辐射量，

是太阳温度，

是地表温度。

而在地球 B 中，太阳辐射被绿叶植物吸收。在吸收等量热量的时候，由于部分辐射能量被用于光合作用，地表的温升就会更低。我们进一步简化我们的假设，认为地表植物全部处于成年期，日间合成的能量在夜间全部通过呼吸作用释放出来，这样在一个昼夜循环后，地球会回到初始状态（如果没有这种简化，我们就要不得不计算地球上化学物质的变化，这样并不能带来 non-trivial 的结果）。那么同样地，夜间所有的热量全部被返还太空。但是，由于在地球 B 中，地表的温升较低，因此夜间返还的温度就会更低，也就是说夜间散失的热量携带的熵流更大。所以太阳辐射经由地球 B 的“加工”，其熵增其实是大于地球 A 的。

因此我们可以看到，地表有植被的情况下，地球在一个昼夜“呼吸”阳光的过程中，造成的熵增更高。因此第二定律其实是“更喜欢”地球 B 的。

我们可以试着在这种计算中增加草食动物、肉食动物、分解细菌等等食物链的环节。最后可以看到，每增加一个环节，会导致熵增更加增加。

11、分形、构形、Lichtenberg 图

下面简单谈一下生物多样性的问题。请注意，以下为私货，如有误导概不负责，请选择性信任！

这是一张闪电图：

这种分支形的图样被称作 Lichtenberg 图。这是一张典型的分形图。在云层电荷击穿大气向着地面放电的过程中，由于电荷传播的自相似性，这就是分形的成因。这种解释是属于“微分”视角的解释：我们跟踪电流路线，对局部进行分解。

但是我们还有一种“积分视角”的解释：这种分支形的电流传播，是放电过程中，空气自适应地形成的电流通量最大的路径。对应着微分角度的分形（fractal），积分角度可以把它叫做构形（constructal，中文是我自己翻译的，可能不准）。这个名称源自 Adrian Bejan 在 1995 年提出的constructal law^[11]:

"For a finite-size system to persist in time (to live), it must evolve in such a way that it provides easier access to the imposed (global) currents that flow through it."（对一个持续变化的有限系统，它的演化使得其结构能让流过其中的流动最容易）。

我们在前面贴的那张分支形的流水图也是同样的构形：流水形成的直流使其流水的阻力最小，流量最大。其他很多类似的支形结构，例如树枝使得水更容易从根部流向顶部；信息传播通过节点 - 分支的形式达到最大速度传播；肺部结构使得气体以最小阻力进入肺泡，……不一而足。

这个定律现在仍有很多的争议，但是已经在很多领域获得应用。Bejan 本人也因此获得了本杰明富兰克林奖章，法国棕榈叶勋章等 N 个国家的高等级奖章。

这个定律给我们的启发是，能量在经过生态圈从低熵态向着高熵态流动的时候，也会有类似的分支形状（constructal）。生物的多样性，恰恰是生物演化以使得整个生态圈以更快的速度耗散能量的结果。

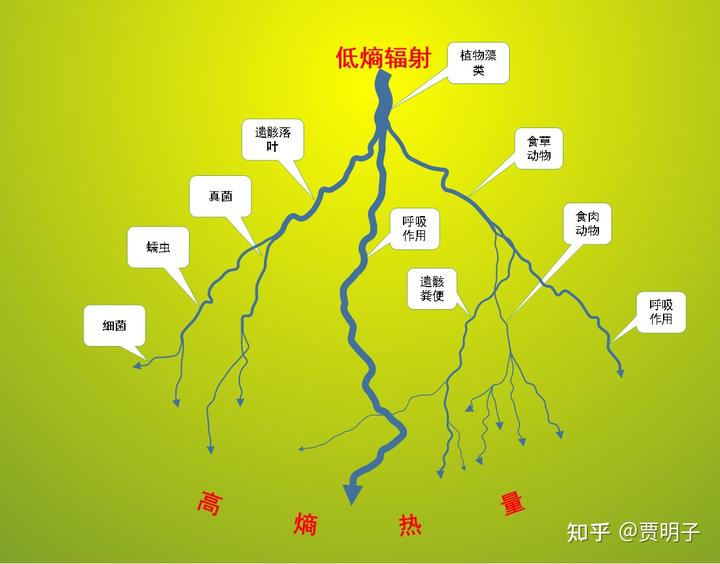
当然，这只是我的脑洞。

更新：“有序”、耗散、Jevons 悖论

讨论区有很多人并没有特别明白这里的逻辑，这里更新一下。

我们考虑一下我们现在的交通网络。它四通八达，规划清晰，绝对是一种高度有序的结构。事实上，从热力学上讲，它肯定也是一种低熵状态（你可以考虑一堆沥青和砂石的混合物，以及一条平整的道路之间熵的不同，更何况道路还有更加宏观的有序结构呢）。这种道路是生物进化到人类这种层次后涌现出来的东西。但是，我可以从两层含义来说明它为何完全符合热力学第二定律：

1、这种有序结构是大量熵增换来的。要知道我们开采石油，炼制，产生沥青；我们开采石块，破碎，产生砂石；我们组织人力，投入大量劳动，最终铺设了这一条条的道路。不论是炼油过程，还是开采过程，还是铺路的过程，都是高度熵增的过程。

2、更加重要的是，这种有序结构的出现导致了能量的更快耗散。这种道路的意义何在？相当一大部分意义就在于让更多的能量耗散者更好地接触到它所耗散的能量。它把更多的人以更快的速度带到能量丰富的地方，同时把更多的能量以更快的速度带到需要耗散能量的地方。比如说，人们从偏远地区开采石油、煤炭、天然气，通过这种交通网络，以任何自然传递（对流、扩散）无法企及的速度运送到需求方（比如说电厂），然后再以极高的速率消耗掉（每年百亿吨），然后再通过同样复杂有序的电网迅速输送至用户端，快速消耗掉。如果没有这种有序的结构，人类根本不可能这么大量地完成能量耗散。

而这种大规模的能量耗散的结果是什么？不是满足了人们的需求，而是更大范围地扩张了人们的需求。从而刺激人们开发更多的技术（建立更多的有序结构）来获取更大的能量消耗。如此一来就形成了一种正反馈效果，把我们的耗散速度不断推高。这就是经济学里面著名的Jevons 悖论。^[12]最终，在表面看起来不断增加的有序度（低熵结构）的背后，是无限扩大的能量耗散。

@王云峰 在评论区里提到戴森球。其实在我看来这是一个很有趣的问题，而不仅仅是一种玩笑和梗。现有的交通网络其实是在一定程度上把“能源猎取”和“能源耗散”之间搭起桥梁，从而极大地加速了熵增。戴森球无疑就是这样一种极致。戴森球看似是一个极度有序的结构，但是它的存在却使得熵增的速度极度放大了。我们未来是否可以实现戴森球尚未可知，但是，我们的未来一定是更高速地获取能量、更高速地分配能量，进而更高速地耗散能量。

更新二：生物多样化的意义

我们可以再回到生态圈的讨论。光合作用以极大的熵增为代价，获取了部分辐射能被固定为化学能。而这部分化学能进而通过呼吸作用以大气温度的热量释放出来，最终完成了全部的耗散。这当然要比地面直接把阳光反射掉的熵产生大得多。

生产者在完成摄取光辐射然后再以呼吸作用把它们释放出来的过程中，无疑是加大了能量的耗散速率的。

那么生态圈中的消费者的意义何在？个人观点，它至少有两个意义：

第一，它打破生产者增殖的 logistic 上限。生态圈中如果没有了消费者，生产者（植物）必然会不断繁衍，最终达到生态资源容量的上限（比如说每平米的光辐射能量所能支撑的植物上限），不再能够继续增殖。消费者把接近上限的容量消耗并最终转化成热耗散掉，从而极大地刺激了生产者的增殖，使得生产者能够更多增殖，因而更多地猎取太阳能。而消费者的比例不能太高，太高的话会降低植物的数量，从而使得它们的增殖不增反减。但是太低的话会使得植物一直处于饱和状态反而降低了它们摄取能量的速度。因而食物链中有一个优化的 1:10 的比例。

第二，它使得能量分配过程极大地优化 - 就像是我们的交通网络一样。消费者可以自由移动，远远超出了一般意义上的自然对流和扩散的速度高得多。在这个过程中，使得能量耗散者能够更容易地接触到能量提供者。我们可以把我们的身体看作是一个个行走的人肉社区。在这个社区中，无数的细胞、微生物共享一个内环境。我们通过捕食活动，把大量的能量通过专门的网络（消化道、血液循环系统、呼吸系统等等）送到各种消费者周围，使得它们可以更容易地接触到资源，进而更快地实现能量耗散。这和交通网络把能源送到电厂，电厂通过电网把能源送达用户如出一辙。（一个类比是，消化道把食物送达肠道，肠道通过血液循环把能源送达各处器官）。这种对“能量耗散者更容易接触到用户”的促进作用极大地增加了能量耗散速度。

同时，消费者把大量的植物迅速变成少量的残渣（粪便、尸体），从而极大地减轻了分解者的负担，使得低效的分解者能够更有效地完成它们的能量耗散过程。事实上，站在食物消化的角度，我们还可以把我们的肠道看作是一种大量分解者协作的协调部门。通过捕食者提供的内环境（肠道）、食物来源（猎取）、残渣处理（排便）、协同信号（激素、消化液等等），无数的分解者得以以更高的效率来分解这些食物。

与此同时，消费者通过自由移动，把植物的种子四处扩散，使其更大规模地分散在更多资源的地区。这种扩散的效率也远远超过对流、扩散这种“自然过程”。这和前面提到的交通网络效果类似：它使得植物能够更加方便地接触到更多的能源。从而加速植被的增殖，进而更多地将太阳能耗散掉。

这就是生物多样性的热力学意义所在：使得能量耗散的速度更快。

更新三：薛定谔错在哪里？

前面提到薛定谔的《生命是什么》，是历史上第一次，也可能是被最广泛引用的一次努力，试图从热力学的角度上解决生命和进化的问题。前面提到，这本著作中无疑有着真知灼见。但是，伟大如薛神也会受限于历史局限。薛神提到生命系统有着一种特殊的能力，就是可以不断从环境中摄取“负熵”进而保持自身的熵值稳定在一个较低的水平。但是薛神的原著中，似乎是认为这是生命的一种特殊能力，甚至于是生命的一种特征。具体机制为何，薛神自己说：

“New laws to be expected in the organism”^[9]

在这里，薛神显然犯了一个错误：他把这种“摄取负熵”的能力看作是生命与非生命的一种典型区别。而事实上，这里并不需要任何一种关于生命器官的“新定律”，它是热力学定律自身的体现。并且，所谓“摄取负熵”的能力也绝非生命独有。自然界中无数的过程和事物都在“摄取负熵”。

我们还是举前面提到的铁棒传热的例子：假设一根细铁棒，它的温度为均匀的 50℃。这时候，我们把它的一端连接一根 100℃的热源，另一端连接一根 0℃的冷源。这个过程中，铁棒内部温度分布就会发生变化，最终稳定在一个线性的温度分布。这个过程如下所示：

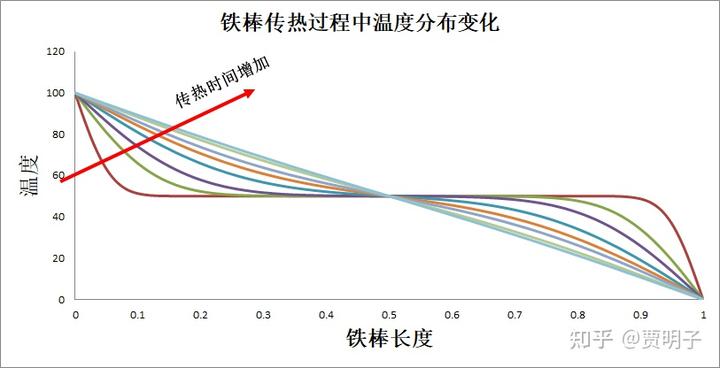
在这个过程中，我们很容易计算铁棒与外界交换的熵流，也就是所谓的“负熵”，以及它自身的熵产生随时间的变化：

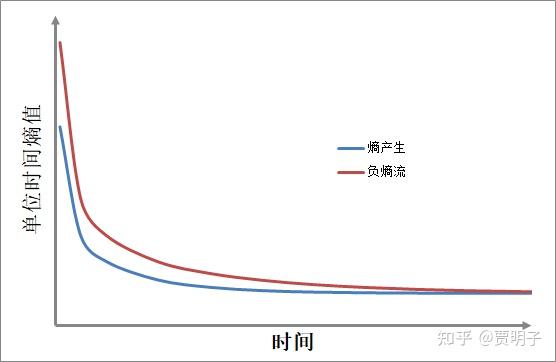
我们可以看到，这根铁棒不断地从外界获得净负熵，而同时自身在不断地制造熵产生。整个过程中，负熵流总是大于熵产生的，因此，铁棒自身的熵值在不断下降，直至达到稳态，熵产生=负熵流的时候，铁棒的熵值也就稳定了：

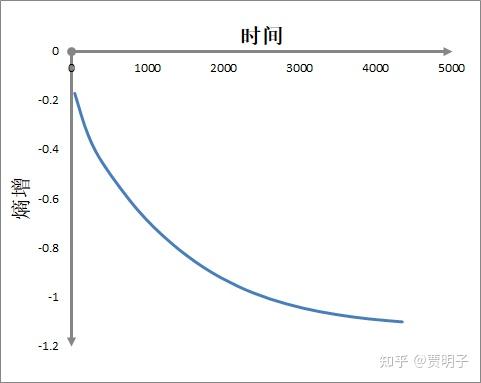
这些都是简单的非平衡态热力学的计算。从中我们可以看到，这根铁棒也有着薛神所猜想的神奇的“摄取负熵”的能力：它不断从热源获得低熵能量，然后向冷源排放高熵能量，从而获得了净负熵。这些净负熵不但抵消掉了自身的熵产生，而且使得自身不断产生熵减！然而就是这么简单的计算，在薛神的时代，在非平衡态热力学尚未得到充分发展的时期，就成了很神奇的东西。

从这个例子我们可以看到，“摄取负熵”绝不是什么生命具有的神奇能力。它只是非平衡态热力学的一种简单现象而已。在特定的非均匀边界条件下，非平衡态的开放系统从外界摄取负熵是一个非常简单的事情，相反地，如果它不能摄取负熵才叫奇怪。

如果讨论区中有更多的有意思的话题，本文将不定时更新。