广义相对论到底有没有解释引力是从何而来的?_网络百科

广义相对论不需要引力这个概念，它把引力给几何化了。怎么理解引力的几何化这个概念呢？你可能听说过引力不是一种真正的力，而是时空的弯曲。注意时空和空间这两个概念是不同的，不能说引力是由于空间扭曲产生的。

对广义相对论最好的归纳是惠勒的一句话：时空告诉物质如何运动，物质告诉时空如何弯曲。地球绕着太阳作椭圆运动，并不是因为地球受到了太阳的引力，地球仍然是按照“直线”运动的，只不过是因为太阳使得周围的时空弯曲了，这个弯曲时空的“直线”以寻常欧式空间的标准来看确实是弯曲了。实际上地球运行的轨迹就是弯曲时空的“直线”。这个弯曲时空的“直线”数学上叫做短程线或者测地线。

如果用严格的数学方程来表示上述过程，就是

$\begin{align*} &R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R =\frac{8\pi G}{c^4}T_{\mu\nu} &(物质告诉时空如何弯曲)\\ &\frac{\mathrm d^2 x^\mu}{\mathrm d\tau^2}+\varGamma^\mu{}_{\nu\rho}\frac{\mathrm d x^\nu}{\mathrm d\tau}\frac{\mathrm d x^\rho}{\mathrm d\tau}=0&(时空告诉物质如何运动)\\ \end{align*}$

当没有太阳存在时(

$T_{\mu\nu}=0$

)，时空是平直的闵可夫斯基空间

$\mathrm ds^2 = -\mathrm d t^2 + \mathrm dx^2+\mathrm d y^2+\mathrm d z^2$

地球沿着直线运动，直线方程是

$\frac{\mathrm d^2 x^\mu}{\mathrm d \tau^2}=0$

，

$x^\mu =v^\mu\tau+a^\mu$

。

当太阳存在时(

$T_{\mu\nu}\neq 0$

)，太阳周围的时空被弯曲了。时空几何为

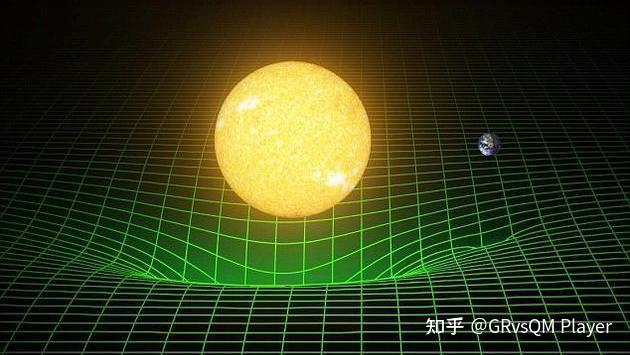
$\mathrm ds^2=-(1-\frac{2m}{r})\mathrm dt^2+(1-\frac{2m}{r})^{-1}\mathrm dr^2+r^2(\mathrm d\theta^2+\sin^2\theta\mathrm d\varphi^2)$

地球沿着弯曲时空里的“直线”运动，直线方程是

$\frac{D^2x^\mu}{D\tau^2}\equiv \frac{\mathrm d^2 x^\mu}{\mathrm d\tau^2}+\varGamma^\mu{}_{\nu\rho}\frac{\mathrm d x^\nu}{\mathrm d \tau}\frac{\mathrm d x^\rho}{\mathrm d \tau}=0$

我们可以比较一下上面的两种情形，没有太阳和有太阳。

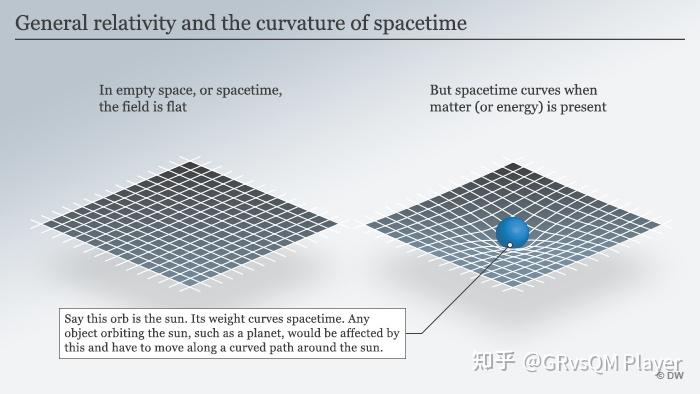
$\begin{align*} &\left. \begin{aligned} &\mathrm ds^2=-\mathrm dt^2+\mathrm dx^2+\mathrm dy^2+\mathrm dz^2\quad(时空)\\ &\frac{\mathrm d^2 x^\mu}{\mathrm d\tau^2}=0，x^\mu =v^\mu\tau+a^\mu \qquad(直线) \end{aligned}\right \}(无太阳)\\ &\qquad\qquad\Large\color{Red}{V}\color{Blue}{S}\\ &\left. \begin{aligned} &\mathrm ds^2=-(1-\frac{2m}{r})\mathrm dt^2+(1-\frac{2m}{r})^{-1}\mathrm dr^2\quad\\ &\quad+r^2(\mathrm d\theta^2+\sin^2\mathrm d\varphi^2)\quad(弯曲时空)\\ &\frac{D^2 x^\mu}{D\tau^2}\equiv\frac{\mathrm d^2 x^\mu}{\mathrm d\tau^2}+\varGamma^\mu{}_{\nu\rho}\frac{\mathrm d x^\nu}{\mathrm d\tau}\frac{\mathrm d x^\rho}{\mathrm d\tau}=0\\&\qquad(弯曲时空的直线) \end{aligned}\right \}(有太阳) \end{align*}$

从这个对比，我们可以发现广义相对论的一大特点，那就是物理学规律在任何参考系下都有相同的形式。如果地球在平直时空是沿着直线运动的话

$\frac{\mathrm d^2 x^\mu}{\mathrm d\tau^2}=0$

，那么在弯曲时空，地球仍然会沿着弯曲时空里的"直线"运动

$\frac{D^2x^\mu}{D\tau^2}=0$

。两种情形下，都没有引力存在。这正印证了开头所讲的，广义相对论不需要“引力”这个概念。

如果我们还怀恋“引力”这个概念，那么要去哪里找到它呢？上文里我们极大地夸张了太阳对周围时空的弯曲，实际上太阳造成的时空弯曲相对于原先的平直时空是微不足道的，以至于地球上未开化的两足兽长时间以为时空是平直的。

$\begin{align*} \mathrm ds^2=-(1-\frac{2m}{r})\mathrm dt^2+(1+\frac{2m}{r})\mathrm d r^2+r^2(\mathrm d\theta^2+\sin^2\theta\mathrm d\varphi^2) \end{align*}$

地球在这个微微弯曲的时空的运动方程是

$\begin{align} &\frac{D^2x^\mu}{D\tau^2}\simeq\frac{\mathrm d^2 x^i}{\mathrm dt^2}+\varGamma^i{}_{00}=0\\ \Longrightarrow& \frac{\mathrm d^2 x^i}{\mathrm dt^2}=-\frac{\partial \phi}{\partial x^i} \end{align}$

Einstein 方程会退化为牛顿引力场方程

$\Delta \phi =4\pi G\rho$

。牛顿引力场方程实际上只是 Einstein 方程时间 - 时间分量的近似。

$\begin{align*} R_{00}\simeq \partial_i \varGamma^i_{00} =\Delta \phi =8\pi G \frac{1}{2}(\rho+\overbrace{3p}^{\simeq0})=4\pi G \rho \end{align*}$

这个微微弯曲接近于平直时空的 Einstein 方程组的矩阵形式如下，

$\begin{align*} \begin{pmatrix}R_{00}\simeq \Delta \phi & 0 & 0& 0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{pmatrix}=8\pi G\begin{pmatrix}\frac{1}{2}\rho&0&0&0\\ 0&0&0&0\\0&0&0&0\\ 0&0&0&0\end{pmatrix} \end{align*}$

从广义相对论还原到牛顿引力论的过程总结如下，

$\begin{align*} \begin{matrix} R_{\mu\nu}& =& 8\pi G S_{\mu\nu}&&\frac{D^2x^\mu}{D\tau^2}\equiv\frac{\mathrm d^2 x^\mu}{\mathrm d \tau^2}+\varGamma^\mu{}_{\nu\rho}\frac{\mathrm d x^\nu}{\mathrm d\tau}\frac{\mathrm d x^\rho}{\mathrm d\tau}=0\\ \downarrow&&\downarrow&&\downarrow\\ R_{00}\simeq\partial_i \varGamma^i_{00}& \simeq & 8\pi G S_{00}&& \frac{\mathrm d^2 x^i}{\mathrm dt^2}+\varGamma^i{}_{00}\simeq 0\\ \updownarrow & &\updownarrow &&\updownarrow\\ \Delta \phi & = & 4\pi G \rho&&\frac{\mathrm d^2 \mathbf x}{\mathrm d t^2}=-\boldsymbol \nabla \phi \end{matrix} \end{align*}$

进阶内容

如果你已经理解了引力的几何化这个思想，那么你一定会好奇其它的力是否也能被理解为某些事物或者几何上的弯曲或者扭曲？答案是肯定，其它力也像万有引力一样，也是某种几何空间的弯曲或扭曲，至少在数学上我们是如此理解的。这种几何叫做纤维丛理论。已经发现的四种基本的力数学上都可以使用纤维丛理论来描述。

一个平凡的纤维丛示例是

$\mathbb{R}^3=\mathbb{R}^2\times \mathbb{R}$

，即我们的 3 维欧式空间。这个平凡的纤维丛有一个底部是二维的平面

$\mathbb R^2$

，数学上叫它底流形

$\mathcal{M}$

。平面

$\mathbb R^2$

上的每个点

$p$

都有一条直线

$\mathbb{R}$

垂直穿过它，这条直线就是

$p$

点的纤维。当然这个示例太过于普通，以至于你可以毫不费力地想象出来。不过如果把

$p$

点的纤维

$\mathbb R$

替换成圆圈⚪呢？So，

$\mathbb{R}^2\times S$

是什么样子？你可以试着在脑子里画一画它的图形，看看它是否是下面这张图所画的样子？

反正答主我脑子太笨了画不出来

$\mathbb R^2\times S$

的图形。不过假如压缩一下底流形

$\mathbb R^2$

为一维流形

$\mathbb R$

，

$\mathbb R \times S$

还是容易想象出来的，它只不过是个躺倒的圆柱面。

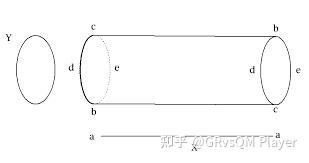
如果把这个躺倒的圆柱面扶起来，我们得到了一种新的平凡的纤维丛

$S\times \mathbb R$

，此时底流形是圆

$S$

，纤维换成了直线

$\mathbb R$

。如果你不喜欢总是用直线

$\mathbb R$

作为纤维，也可以选择圆

$S$

作为纤维。

$S\times S$

的图形是轮胎面。

上面举的例子都是平庸的，所谓平庸指的是将底流形

$\mathcal M$

整体的和纤维

$F$

之间作个直积

$\mathcal M\times F$

。我们也可以取底流形

$\mathcal M$

局部的一小部分

$U$

和纤维

$F$

作直积，再将

$U\times F$

按某种方式粘连起来。比如，只有一个面的莫比乌斯带和圆柱面有相同的底流形

$S$

和纤维

$F$

。

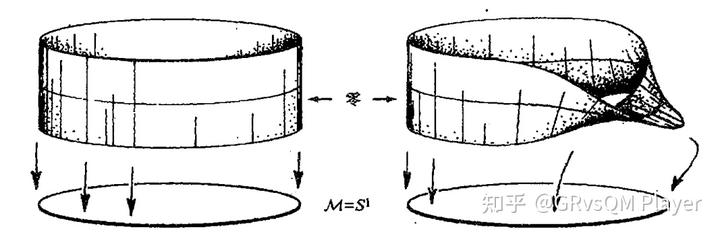
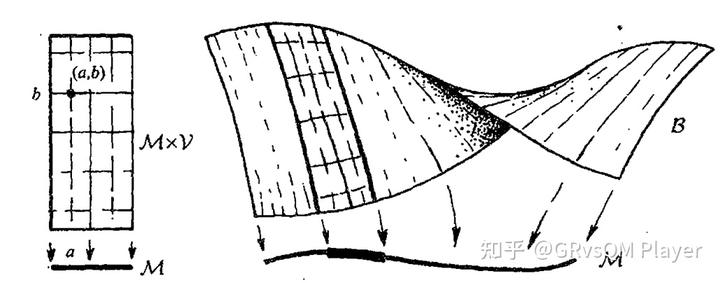
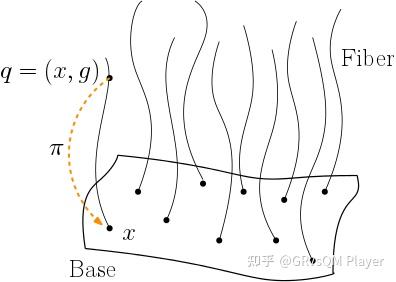
一个纤维丛有五个要素，可以用个五元组

$(\mathcal{M}, F, \pi, G,\mathcal{P})$

来表示，

$\mathcal{M}$

是底流形，也就是物理学所说的时空，

$F$

是底流形上某个点

$p$

的纤维，时空上各个点的纤维

$F$

本质上是相同的，

$F_x \simeq F_y$

，

$F$

可以是某点的所有切矢量组成的切空间，也可以是该点的局部正交变换构成的转动群，也可以是其它奇怪的东西；时空

$\mathcal{M}$

上的每个点及每个点上的纤维组成了全空间

$\mathcal{P}$

，

$\pi$

是全空间

$\mathcal{P}$

投影到底流形

$\mathcal{M}$

上的映射

$\pi: \mathcal{P}\to \mathcal{M}$

，结构群

$G$

告诉我们纤维丛是如何粘连起来的。

非平庸的纤维丛的图像是很难在纸上画出来，但是在局部上它的结构非常简单，是个直积

$U\times F$

。

物理学上所用到的是一种特殊的纤维丛，它在局部上是

$U\times G$

，也就是说它的纤维

$F$

就是结构群

$G$

。数学上把这种纤维丛称作主丛。所谓的群数学上是一种保持乘法

$\circ$

运算封闭的代数结构，它有单位元

$I$

（

$g\circ I =I\circ g$

），每个群元素

$g$

都有逆元素

$g^{-1}$

（

$g\circ g^{-1}=I，g^{-1}\circ g=I$

），任意两个群元素

$g$

$g'$

相乘后得到的新元素

$g\circ g'$

仍然属于群，并且对乘法

$\circ$

保持结合律，即

$(g_1\circ g_2)\circ g_3 =g_1\circ (g_2\circ g_3)$

。

物理学家们使用群来描述系统的对称性。根据诺特定理，每一种连续对称性都对应着一种守恒律。比如假如系统不随时间变化，那么

$t$

时刻的物理量

$f$

等于

$t+a$

时刻的物理量

$f(t+a)$

。这相当于

$f$

沿着时间轴平移了

$a$

个单位。时间平移不变性所对应的物理学守恒律是能量守恒。类似的，关于空间的平移不变性对应着动量守恒，关于空间的转动不变性对应着角动量守恒。以上列举的这些对称性都是时空上也就是底流形

$\mathcal{M}$

的对称性，除了这些时空对称性外，还有一些和时空对称性无关的对称性。其中一种是电荷守恒所对应的规范对称性。在电动力学里，电场

$\mathbf E = -\boldsymbol \nabla \phi -\frac{\partial \mathbf A}{\partial t}$

和磁场

$\mathbf B =\boldsymbol \nabla \times \mathbf A$

的定义存在一定的冗余性，将

$\mathbf A$

替换为

$\mathbf A +\boldsymbol \nabla \psi$

，

$\phi$

替换为

$\phi -\frac{\partial\psi}{\partial t}$

，并不会改变电场

$\mathbf E$

和磁场

$\mathbf B$

，这里

$\psi$

是任意函数。

只要我们知道了局域的内部对称群是什么，就能写出这个内部对称群所对应的相互作用，也就是力的形式。让我们从一个自由电子的作用量开始，它的拉格朗日密度是

$\begin{align*} \mathcal{L}_{电子}=\overline\Psi i\gamma^\mu\partial_\mu \Psi -m\overline \Psi \Psi \end{align*}$

对电子的场

$\Psi$

作关于内部对称性群

$U(1)$

的变换，

$\Psi \to e^{-i\theta(x)}\Psi$

，那么自由电子的拉式量并不是不变的，

$\mathcal L'_{电子}\neq \mathcal L_{电子}$

。

$\begin{align*} \mathcal{L}'_{电子}&=\overline \Psi e^{i\theta}i\gamma^\mu \partial_\mu (e^{-i\theta}\Psi)-m\overline \Psi\Psi \\ &=\overline \Psi i\gamma^\mu \partial_\mu\Psi -m\overline\Psi\Psi+\overline \Psi \gamma^\mu \partial_\mu \theta(x)\Psi\\ &\neq \mathcal{L}_{电子} \end{align*}$

要想让电子场

$\Psi$

的拉式量保持关于内部对称性群

$U(1)$

的不变性，需要引入光子的场

$A_\mu$

，并且光子的场

$A_\mu$

，要按照

$A'_\mu=A_\mu +\frac{1}{e}\partial_\mu \theta(x)$

规则进行变换。

$\begin{align*} \mathcal L'_{电子}&=\overline\Psi e^{i\theta}i\gamma^\mu (\partial_\mu+ie A'_\mu) e^{-i\theta}\Psi\\ &=\overline \Psi i\gamma^\mu(\partial_\mu+ieA'_\mu-i\partial_\mu\theta)\psi -m\overline \Psi \Psi\\ &=\overline \Psi i\gamma^\mu(\partial_\mu+ieA_\mu)\Psi -m\overline \Psi \Psi\\ &=\mathcal{L}_{电子} \end{align*}$

和自由电子的拉格朗日密度相比，在局部

$U(1)$

群变换下不变的拉格朗日量多了一项

$A_\mu J^\mu$

，它正是电子场和光子场

$A_\mu$

的相互作用项，

$J^\mu$

是四维的电流。

$\begin{align*} \mathcal L'_{U(1)不变}&=\overline \Psi i\gamma^\mu D_\mu \Psi -m\overline \Psi \Psi \\ &=\overbrace{\overline \Psi i\gamma^\mu \partial_\mu \Psi -m\overline \Psi \Psi}^{自由电子} +\overbrace{A_\mu (\underbrace{-e\overline\Psi\gamma^\mu \Psi}_{电流J^\mu})}^{电子和光子的力} \end{align*}$

和质量在广义相对论里的作用一样，电荷的存在扭曲了底流形闵可夫斯基空间

$\mathbb M_4$

和它上面的纤维

$F=U(1)$

共同组成的整体的直积空间

$\mathbb M_4\times U(1)$

，现在这个空间不再是

$\mathbb M_4\times U(1)$

的样子，而是完全扭曲的局部像

$\mathbb M_4\times U(1)$

的纤维丛空间

$\mathcal P$

。电子和光子之间的电磁力正像引力来自于弯曲的时空

$\mathcal M$

一样，从扭曲的纤维丛

$\mathcal P$

显现出来，生活在底空间

$\mathcal M$

上的智慧生物将会发现一种截然不同于万有引力的力，即电磁力。法拉第场强

$F_{\mu\nu}=\partial_\mu A_\nu -\partial_\nu A_\mu$

刻画了这纤维丛

$\mathcal P$

的扭曲程度。它起着类似于广义相对论时空曲率

$R^\mu{}_{\nu\rho\sigma}$

一样的作用。

包含电子场和光子场的完整的拉格朗日密度是

$\begin{align*} \mathcal{L}&=-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}+\overline\Psi i\gamma^\mu D_\mu \Psi-m\overline\Psi\Psi \\ &=\overbrace{-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}}^{曲率项}+\overline \Psi (i\partial\mkern-10.5mu/-m)\Psi+\overbrace{\underbrace{A_\mu}_{媒介子} (\underbrace{-e\overline\Psi\gamma^\mu\Psi}_{源} )}^{电磁力} \end{align*}$

式中的曲率项

$-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}$

是自由的光子场的拉格朗日密度，它也是关于局部

$U(1)$

群不变的。将

$F_{\mu\nu}=\partial_\mu A_\nu -\partial_\nu A_\mu$

代入曲率项，可以得到

$\mathcal L_{光子}=-\frac{1}{4}(\partial_\mu A_\nu-\partial_\nu A_\mu)^2$

，这是自由光子的拉式密度。上式的第三项是电子和光子的相互作用项，也就是电磁力的微观形式。在量子场论里，这一项叫做顶角项。电子和光子只有这么一种顶角。式中的

$-e$

是电子所携带的电荷，电量是

$e$

，最小的基本电荷，

$-$

表示负电荷。对

$A_\mu$

变分，可以得到符合狭义相对论的波动方程

$\Box A^\nu -\partial_\mu\partial^\nu A^\mu=e\overline \Psi \gamma^\mu \Psi$

。从中可以看出源对于电磁场

$A^\nu$

的影响是相对论性。在宏观上，总是取推迟解，即

$A^\mu =\int \frac{J^\mu(t-|\mathbf r-\mathbf r'|)}{|\mathbf r-\mathbf r'|}\mathrm d^3\mathbf r'$

，即场的变化总是落后于源的变化。电磁场

$A_\mu$

可以独立于源

$J^\mu$

存在，这就是我们通常所说的电磁波。

电磁力所对应的局部对称群

$U(1)$

，它的两个群元素

$g_1$

、

$g_2$

之间是可以改变乘法顺序的。1954 年，杨振宁和他的学生米尔斯引入了一种全新的局域内部对称性群

$SU(2)$

。它的群元素是不可改变乘法顺序。这种不可交换的特性带来了有别于电磁场的新的有趣性质，那就是电磁场的源只能是电荷，电磁场本身是电中性的，并不携带电荷。Yang-Mills 场本身可以作为自身的源，产生新的 Yang-Mils 场。和电磁场

$F_{\mu\nu} =\partial_\mu A_\nu -\partial_\nu A_\mu$

对比，Yang-Mills 场

$\mathfrak f_{\mu\nu}=\partial_\mu \mathfrak b_\nu -\partial_\nu \mathfrak b_\mu +\mathfrak b_\mu \times \mathfrak b_\nu$

有自相互作用项。尽管原始的 Yang-Mills 场在物理上是不正确的，但是它所蕴含的局域化对称性思想以及背后的数学结构今天已经被证明是完全正确的。标准模型里的出现的力都可以写成 Yang-Mills 场的形式。

$\begin{equation*} \left.\begin{aligned} \mathcal{L}_{SM}&= \overbrace{-\frac{1}{4}G^a_{\mu\nu}G^{a\mu\nu}}^{强核力(色力)}\overbrace{-\frac{1}{4}W^i_{\mu\nu}W^{i\mu\nu}-\frac{1}{4}B_{\mu\nu}B^{\mu\nu}}^{电磁力+弱核力}\\ &\quad+\overline L iD\mkern-10.5mu/ L+\overline \nu_R i\partial\mkern-10.5mu/ \nu_R+\overline e_R iD\mkern-10.5mu/ e_R \\ &\quad+\overline Q iD\mkern-10.5mu/ Q+\overline u_R iD\mkern-10.5mu/ u_R+\overline d_R iD\mkern-10.5mu/ d_R\\ &\quad\overbrace{+(D_\mu\Phi)^\dagger D^\mu \Phi +\mu^2 \Phi^\dagger\Phi -\lambda (\Phi^\dagger\Phi)^2}^{上帝粒子或Higgs玻色子}\\ &\quad+\Gamma^{(\nu)} \overline L \widetilde\Phi \nu_R+\Gamma^{(e)}\overline L \Phi e_R+h.c.\\ &\quad+\Gamma^{(u)} \overline Q \widetilde\Phi u_R+\Gamma^{(d)}\overline Q \Phi d_R+h.c. \end{aligned} \right \} 标准模型 \end{equation*}$

上式中的

$G^a_{\mu\nu}$

与

$W^i_{\mu\nu}$

就是 Yang-Mills 规范场的场强，和电磁场的法拉第场强

$F_{\mu\nu}$

的区别在于存在自相互作用项。

$\begin{align*} F_{\mu\nu}&= \partial_\mu A_\nu -\partial_\nu A_\mu\\ W^i_{\mu\nu}&= \partial_\mu W^i_\nu -\partial_\nu W^j+g_W\epsilon^{ijk} W^jW^k\\ G^a_{\mu\nu}&=\partial_\mu G^a_\nu -\partial_\nu G^a+g_C \lambda^{abc}G^b_\mu G^c_\nu \end{align*}$

$W^i$

里的上标

$i$

取 1、2、3 表示弱核力的媒介子有三个，

$G^a$

里的上标

$a$

取 1 到 8 表示色力的媒介子有八个。电磁力、弱核力、色力的区别仅仅是内部的对称群

$G$

不同。现在使用局域化对称性的思想，我们可以重新认识万有引力。万有引力的局域对称性群是时空的伪正交群

$SO(1,3)$

，它的场强是

$\begin{align} R^{ab}{}_{\mu\nu}=\partial_\mu \omega^{ab}{}_\nu -\partial_\nu \omega^{ab}{}_\mu +\omega^a{}_{c\mu} \omega^{cb}{}_\nu-\omega^a{}_{c\nu}\omega^{cb}{}_\mu \end{align}$

使用嘉当的公式可以极大的简化上述公式，所有这些力的场强可以统一写作

$F=\mathrm d A+A\wedge A$

它在数学上的意义是纤维丛

$\mathcal P$

的曲率，也就是刻画纤维丛

$\mathcal P$

如何扭曲偏离于整体的直积丛

$\mathbb M_4\times G$

。不过对于引力的情况，除了服从一般的纤维丛的曲率公式

$F=\mathrm d A+A\wedge A$

，还有额外的约束条件

$T =0$

，

$T:=\mathrm d e +e\wedge \omega$

是挠率。广义相对论的时空都是没有挠率，也就是说引力只是时空的弯曲效应，而不是时空的扭曲效应。这样说明了为什么其它力无法通过局部的加速参考系消除。

我们列出引力和电磁力、弱力、色力所对应的几何：

$\begin{matrix} & 平的空间 & \begin{matrix}弯曲或扭曲\\的空间(纤维丛)\end{matrix} & 联络 & 曲率 & 源\\ 引力& \mathbb M_4 & \mathcal{M}_4(时空) & \varGamma^\mu{}_{\nu\rho} & R^\mu{}_{\nu\rho\sigma}& \begin{matrix}能量\\（物质或引力）\end{matrix}\\ 电磁力& \mathbb M_4\times U(1)& \mathcal P_{U(1)} & A_\mu &F_{\mu\nu}& 电荷\\ 弱核力& \mathbb M_4\times SU(2)& \mathcal P_{SU(2)}&W^i_\mu &W^i_{\mu\nu}&弱荷\\ 色力 & \mathbb M_4\times SU(3) & \mathcal P_{SU(3)}& G^a_\mu & G^a_{\mu\nu} &色荷 \\ 引力* &\mathbb M_4\times SO(1,3) &\mathcal P_{SO(1,3)} &\omega^{ab}{}_\mu &R^{ab}{}_{\mu\nu}& 同一 \end{matrix}$

广义相对论到底有没有解释引力是从何而来的?

相关推荐