刚看到这个问题时,我在想:投影、最小二乘法、回归、SVD、PCA、图像处理、优化、机器学习、密码学……这些全都要用矩阵啊。
但是我转念一想,好像矩阵确实不是必需的:
假设 A 是一个
的矩阵, 那么
可以写作
假设 B 是
的矩阵,那么矩阵乘法
可以写作
当然,行列式
也是可以表示出来的
其中
是 n 阶对称群。
当然,有了行列式,就可以定义"伴随矩阵"
那么,"逆矩阵"的公式就有了:
所以,我们线性代数课上学过的
,就可以表示成
这样下去,其实任何需要矩阵的地方,都可以不使用矩阵列出公式。
有些常用的计算,比如“最小二乘法”的公式,是这样的:
其中 A 是
的矩阵,很多高赞都提到了这个公式,它可以用来做线性回归,在统计学和数据科学中都有很多应用。
但是,经过我们刚才的一番推导,我们发现,这个式子其实也可以不用矩阵写。我们现在可以尝试把它翻译一下,写成不需要矩阵的形式。翻译过后,它差不多大概长这样:
算得不一定对。但是基本意思大家都能明白:这个式子太复杂了!!
而且,实际应用中,你还不能直接用这个式子,因为它的计算量太大了!为了让计算机更快地算出答案,你还要“化简”上面这个式子,找到能让计算机快速算出答案的算法。
来吧!化简这个式子!

这里举一个更简单的例子:大家有没有想过,为什么人类要发明乘法?
为什么不写做(5+5+5+5)呢?乘法的发明到底简化了哪些问题?
确实,乘法本身好像并没有解决任何问题,更复杂的乘法,比如
,也可以表示成加法的形式
然而,没有人愿意计算[(5+5+5+5)+(5+5+5+5)+(5+5+5+5)] + [(5+5+5+5)+(5+5+5+5)+(5+5+5+5)],但如果你学过乘法,你可以很快算出
。
事实上,“让复杂的公式变得简洁起来。”本来就是一件很重要的事情。因为,它能精简人们的思维,让人们更容易发现问题的关键,然后去探索更加深奥的问题。
在简化这些式子的途中,我们还能发现很多新的问题。乘法一开始只是在化简“同一个数字连加”的问题。但是,随着乘法使用得越来越广泛,人们开始关注更加深奥的问题,比如
这种乘法,就不是某种“同一个数字连加”的问题。
线性代数其实也可以被推广到更广泛的形式,不过实际应用中比较少见。
比如 @Bazinga 就提到了线性空间和线性算子。感兴趣的朋友还可以自行搜索一下度量空间、赋范空间、内积空间、埃尔米特伴随算子。
然后我们回来看刚才的“最小二乘法”。
我们知道,所谓最小二乘法,就是找到一条线,使得误差的平方之和最小。
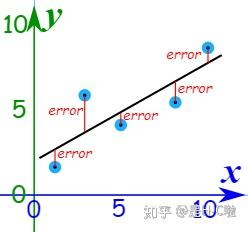
那么,如果我们不去最小化“误差的平方值和”,换一个优化目标,那么我们还有没有
这样的式子呢?
事实上,你会发现,优化“误差的平方值和”其实就是在优化真实值与预测值之间的欧几里得距离,也就是 l2 距离。而这个 l2 范数是以向量点乘为内积诱导出来的。而在使用向量点乘为内积的实向量空间中,我们有
。
其实,我们可以有一个更广义的“最小二乘法”,它将作用于任何一个内积空间中,它就是
。其中
是
的埃尔米特伴随。而此时这个 x 所最小化的目标,就是在这个内积空间所诱导出来的度量空间中,真实值与预测值之间的距离。
在实内积空间中,我们有
,这个式子就是
.在复内积空间中,我们有
,这个式子就是
。再其它内积空间中,
,这个式子仍然还会成立。
实内积空间上的
或许还能用初等代数勉强代替一下。但是,抽象的内积空间上的“最小二乘法”,也就是
,大概是不能用初等的代数代替的。
就像
不能用加法来表示一样。

 微信扫一扫
微信扫一扫 



