题主这个问题,问得相当好,相当有深度,可惜,问得迟了点,经计算,迟了 156 年。
因为,英国物理学家麦克斯韦也曾遇到这个问题,并由此经过一系列的天才的数学抽象和物理归纳,于 1865 年,创立了伟大的麦克斯韦方程,非但解决了这个问题,而且建立起了宏伟的电磁学理论大厦,并预言了电磁波的存在。
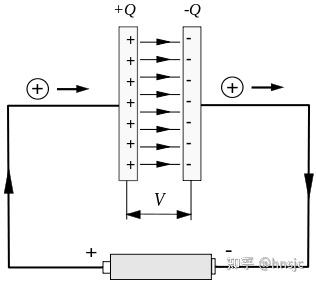
观察上图的电容充电电路,导线上流动的是最常见的传导电流。但在电容器的两极板之间,是没有电流的,电荷只传导到电容的正负极板,没有电荷穿越极板间空间形成电流。
19 世界中期,人们已经掌握了电磁场的一些理论,掌握了电生磁和磁生电的方法,后续也发明了电动机和发电机。只要是电流,就能产生磁场,因此电容充电时,电流流过导线,导线周围就有磁场。对"通电导线产生磁场"这种因果关系,当时安培搞了个数学公式,叫安培定律:
这个定律的物理含义是:电流
产生了磁场
,且成正比关系。如果说电流是“因”,那么磁就是“果”。公式在数学上,有严密的限定:“闭合积分路径
”应该是“构造曲面
”的边界,而电流
则必须是穿过“构造曲面
”的。
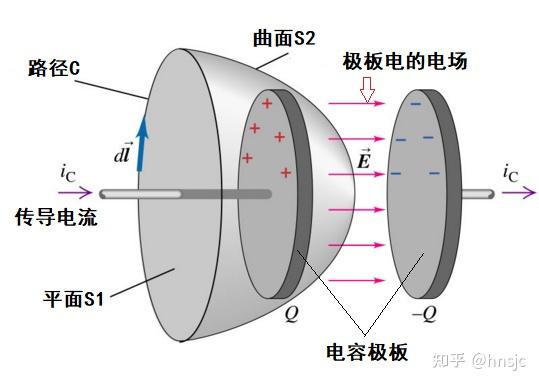
“构造曲面
”,是任意选的,与要考察的空间位置有关。比如上图中,选择平面 S1 为构造曲面,它的边界线是路径 C,绕一圈对磁场 B 积分(图中蓝色箭头
代表微分长度)得到的所谓“环量”,就正比于电流
。安培定律是经过数学家和物理学家的论证,定律本身是无懈可击的。
但在电容器充电电路的分析中遇到了一个困难:因为构造曲面是任意的,如果不选平面 S1,而是选一个曲面 S2,曲面 S2 是包围了电容器的一块极板的“袋子”,这时会发现,路径 C 没变,但电流
竟然没有穿过曲面 S2。同一个公式,选 S1 时成立,选 S2 时竟然不成立了?麦克斯韦陷入了沉思……
解决这个问题,还是要着眼于电容器内的极板空间,极板间有什么东西呢?充电时,极板上建立起一个电场,注意这个电场在充电过程中是随时间变化的。电流越大,充电越快,电场也建得越快,可见电场建立的快慢与电流的大小有关!电场的变化快慢可以用 “电场通量的时间变化率“来表示 ,数学上可写作:
,这是一个微积分表达式,表示先对电容器极板电场求通量(电场
乘以面积
),再求通量的时间变化率(除以微分时间
),
是一个常数。
那么电场通量的时间变化 率,与电流
有什么关系呢?麦克斯韦马上动手,七七八八一算,发现一个重大奥秘:这个量的物理单位,竟然与电流完全一样!因此,可以把它看作是一种不同形式的电流!麦克斯韦专门给它取了一个名字,叫“位移电流”。麦克斯韦同时认为:这个“电场通量变化率”,既然与电流一样,当然也能产生磁场。这个结论 ,就是“变化的电场可以产生磁场” 。据此,麦克斯韦把著名的安培定律修改成:
等式右边,在原来电流
项后,增加了第 2 项“时变电场”,从而完善了安培定律,这是麦克斯韦的重大发现。这个等式就成了更加著名的“安培 - 麦克斯韦”定律。再加上人们之前就发现的 3 个电磁学定律“高斯电场定律、高斯磁场定律、法拉第定律”,组成了名震江湖的“麦克斯韦方程”。
表面上看,麦克斯韦只贡献了第 4 个方程中的第 2 项,相当于半个公式,但最终凭这半个公式,麦克斯韦补全了整个电磁学理论最后一根柱子 。 有了这第 2 项,打通了“时变电场”通向“时变磁场”的任督二脉,电场和磁场不再孤立,只要“时变”,他俩就能相互转换,生生不息,形成电磁波,向无限空间传播。电磁波,曾经梦幻一般的神话,硬是被麦克斯韦抓到科学技术的箩筐中了,无线电通讯,可以说呼之欲出 。
不过名震江湖是后来的事了,麦克斯韦当时建立整套方程并预言电磁波后,没几人看得懂,加上当时没有获得快速时变电场的仪器,实验室里也做不出结果来。不过说没几人看得懂,并不是当时人们没水平,而是因为矢量微积分这套工具还没有创立。沉寂了 20 年后,赫兹才做成了电磁波实验。随着后续理论探索、研究发明劈里啪啦不断进行,人类文明就诞生了无线电通信,再后来,我们就用上了电脑和手机。
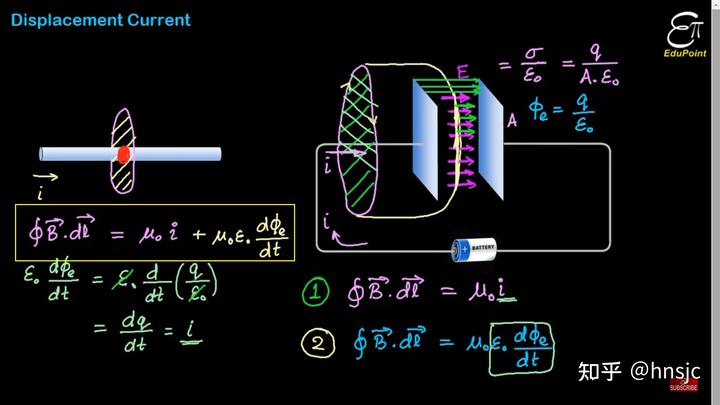
这是较为详细的分析图,含义如前所述,不再详述。

 微信扫一扫
微信扫一扫 



