1、为何常规的解释并不能解释什么
这个问题可以抽象地说,也可以直观地说。抽象说只需要一句话,直观说需要一大篇。抽象的说法大家都知道了,反倒是直观的说法大家还不太熟悉。
我想从直观的角度来说一说这个问题。
首先,评论一下题主的问题,
不要说,因为沸点是液体的饱和蒸气压与外界气压相等时 对应的温度。
但是事实上,这基本上就是这个问题的一半答案了。
题主的这句话隐含了一个关键信息,就是系统的自由度:在外界压力(在纯组分系统,外界压力就是蒸汽压)一定的时候,沸点是一个定值。也就是说,沸点是随着压力的确定而确定的,沸点是压力的函数。
所以,反过来,如果温度确定了,气液平衡的系统压力也就确定了。这个压力就是饱和蒸汽压。
所以,问题就是,在气液两相的纯组分平衡系统,系统只有一个自由度。我们可以谈论某个压力下的沸点,反之也可以谈论某个温度下的蒸汽压。
那么,为何、又是如何出现气液两相平衡的呢?
一个非常常见的,关于蒸汽压的解释是这样的:
- 在沸腾的时候,存在着气液两相的动态平衡。
- 在动态平衡中,液相的水分子脱离液态的束缚进入气相,气相的自由分子被液相束缚而进入气相,这两者恰好相等,因此总体上气液两相共同存在。
- 在高压的时候,气相的自由分子进入液相的速率增加,打破平衡,宏观上就是蒸汽的冷凝;反之,则是水的蒸发。只有在蒸汽压的情况下,蒸发和冷凝达到平衡。
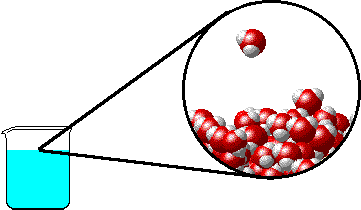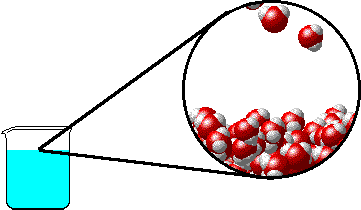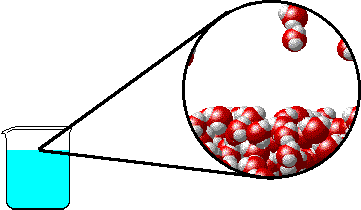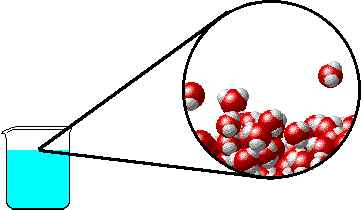
这是大家耳熟能详的解释,看似挺有道理的。
但是这个其实并不能回答任何问题。原因是,这个说法压根儿就不能解释“为什么就会有气液两相的区分”。在这个说法里,我们其实是假定了“存在着气相和液相两种不同的相态”,然后才说在某个特定的压力下,这两相可以并存。而题主的问题,其实可以分解成两个问题:
- 为何会有两种不同的相态并存?
- 为何在两种相态并存的时候,有一个固定的平衡压力(饱和蒸汽压),这个压力是多少?
下面的解释,基本上采用经典分子动力学的视角。
首先,我们来考虑这样一个问题:一堆水分子(我们先不去管它们处于何种相态),它们有很大的动能,四处飞窜,频繁碰撞,那么是什么原因能够让它们聚集在一起,而不是完全脱离,到处逸散的?
2、系统的内部平衡
一堆水分子之所以能够聚集在一起,可能的原因有两个:
一个是,水分子之间的相互作用力,具体讲,就是它们存在着相互吸引的作用力,使得它们聚集成团;
第二个是,外界的压力。具体讲,就是有一个“容器”把它们限制在了一起(或者是万有引力把它们束缚在一起),这个容器对这一堆水分子施加了一定的压力,抵消了水分子的“逃窜”。
我们不妨来看一看,一个对这个状态的一个简化的描述——范德华方程,这个方程是这样的:
如果对这个方程做一个直观化的解读,那么这个公式其实说的是这个意思:
外界压力(束缚力)=分子间的“斥力”- 分子间的吸引力
我们知道,分子间存在的相互作用力包括了引力和斥力两种。它们之间的斥力只有在两个分子相互靠近得非常近的情况下才发生。也就是说,我们可以近似地把它当作是一个硬球。两个分子只有在碰撞的时候,才会产生一个瞬时的力,只要是它们不接触,就不会发生斥力。(也就是一个无限高的势垒)。
在硬球的碰撞产生的“斥力”之外,分子间还存在着延伸一定距离的引力作用。这种引力它随着距离的增加连续减弱,而当分子达到一定距离之后,它会衰减为零。也就是说,当分子足够靠近(但是还没有相互碰撞)的时候,它们之间相互吸引,但是距离较远后,这种吸引力就渐渐消失了。相对斥力而言,它是一种长程力,因为它不是“接触力”,但是它也是一种短程力。事实上,它随着分子距离的六次方衰减。

现在,我们就可以仔细掰扯一下上面公式中的三个力:
1、分子间的斥力,是它们作为“硬球”不断地发生碰撞所产生的一力。由于分子总是在无休止地做热运动,它们总是在不断地发生碰撞。在任何一个持续很短的时间内,总有若干的分子与边界碰撞,从宏观上就形成了连续的对边界向外“排斥”的力。这种力的大小正比于温度(因为温度越高,碰撞越激烈)和密度(因为密度越高,碰撞越频繁)。
2、分子间的引力,则是当分子的密度足够大,靠得足够近的时候,产生的静电吸引力(现实情况会复杂得多,会有诸如氢键之类)。这种力虽然弱,但是是有一定的作用距离的。当分子的密度足够大、分子间的平均间距足够小的时候,才会有宏观效应。
于是乎,这就是一个简单的受力平衡。斥力使分子们向外逸散,而引力使分子们聚集在一起。我们把一堆水分子束缚在一起所需要给它施加的压力,就等于它们之间的相互斥力减去它们之间的相互吸引力。
3、短程力和平衡失稳
请注意,这里所说的“斥力”并不是两个单独分子之间的斥力。这种斥力只有在两个分子互相靠的非常近的时候才有(用硬球模型,就是只有碰撞的时候才有)。这里所说的斥力,指的是大量分子相互碰撞的统计平均。由于斥力是无限高势垒,他最终就取决于碰撞频率和强度,它的影响就是长程的。而吸引力则是短程力,在分子间相互靠得比较近的时候它起作用,在远离的时候可以忽略。
所以说,斥力总是会有的,因为分子之间总是在不停碰撞的。但是吸引力却不总是有。当分子间距较大的时候,吸引力就弱到可以忽略了。所以,在气体状态下,分子间的吸引力几乎完全没有,这些分子就像是弹性硬球一样,只有因为碰撞而产生的斥力。这时候,外界压力就等于斥力。这就是理想气体。
而在分子间互相靠得非常近的时候,它的影响又会远远小于斥力(再次强调斥力是无限高能垒),此时它仍然是一种可以被忽略的状态。此时还是有外界压力就等于斥力。这就是液态。
我们可以看到,当引力作用可以忽略的时候,上述平衡就是一个一次方程。也就是有且仅有一个解。也就是说,在稀薄和致密的情况下,都只会有一种状态存在:液态或者气态。
但是,当在稀薄和致密之间的过渡状态下(也就是在相态转换的过程中),引力不可忽略的时候,上述平衡就是一个三次方程。那么就可能会出现三个解的时候。
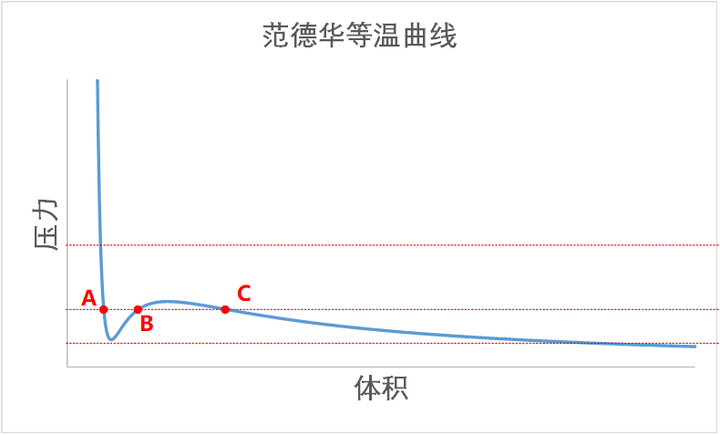
上图中,左侧的 A 点是致密状态,就是稳定的液相,右侧的 C 点是稀薄状态,就是稳定的气相,那么中间的 B 点呢?B 点是一个不稳定的点。
怎么理解 B 点的不稳定呢?因为 B 点有着负压缩率。所谓的负压缩率,指的是,你越用力压缩,它就膨胀的越厉害。而你越不压缩它,它收缩得越厉害。这是一种正反馈效应。比如说:
- 当我们减轻对体系的压缩,会导致体系收缩。
- 而体系的收缩,就会进一步减少对外界的压力,根据牛三,也就是减少自身的压力。
- 而减少的自身压力会进一步导致自身的收缩。
- 循环回到 1.
这样一来,一个微小的扰动就会打破平衡。使得 B 点崩塌,要么迅速膨胀到 C 点,要么迅速收缩到 A 点。也就是说,B 点实际上是不存在的。
从微观上讲,这个正反馈效应就是这样的:
- 分子间相互靠近一点,会导致引力的增加,打破平衡。
- 引力的增加会更加拉近分子间的靠近。
- 进一步的靠近会导致引力的进一步增加
- 循环回到 1.
或者反过来:
- 分子间相互远离一点,会导致引力的减小,打破平衡。
- 引力的减小会使分子间更加排斥,增加距离。
- 进一步的远离会导致引力的进一步减小。
- 循环回到 1.
所以说,从气体到液体,就必然有一个过渡的过程,这个过程中存在两个稳定的状态,也就是气液共存的状态。这个过渡态,就会有致密相和稀薄相两种截然不同的相态并存。
在这个过渡区的压缩过程中,和纯气态和纯液态很不同。气态和液态的压缩,都是均相的,它们的密度被均匀压缩。但是过渡区中,那个均匀压缩的解(也就是 B 点)是不稳定的,所以,就是两个不同的相被压缩,压缩过程中,不断增加的是平均密度。而这个平均密度的变大,是液体比率不断增加实现的,而不是整体被均匀压缩实现的。
这就回答了第一个问题:为何会有两种不同的相态并存?
4、自由度
那么我们来看第二个问题:既然中间的过渡阶段只能有两相共存,而不存在两相间的某种均相状态,那么在这个过渡过程中,为何有一个不变的平衡压力(饱和蒸汽压),这个压力是多少?
当然,我们根据实验现象知道,在相转换的过程中,在等温条件下,我们不断加压的过程中,并不会导致压力的上升,而是会导致气体不断冷凝。也就是说,我们对气体的加压被气体冷凝给“吃掉了”。
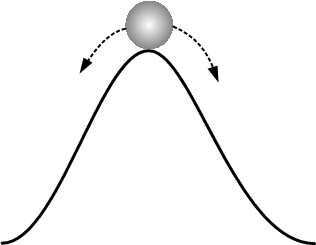
也就是说,当温度确定时,两相转换过程中,压力不变。这个压力就是饱和蒸汽压。此时,范德华方程预言的下图中虚线的压缩曲线,在实际中是这样一条水平的直线。
这是一个观测得到的现象。

我们现在需要对这个现象提出一个解释,为何在确定的温度下,相转换过程的压力不变(等效地说,为何在确定的压力下,沸点不变)?这个问题其实在第一个问题有了答案后,就立刻可以解答了。那就是相律。
我不打算推导相律。只是对本题做一个说明。
在单相的情况下,系统有两个自由度。比如说,我们可以任意变化它的温度和压力。在温度确定后,系统就只有一个自由度了。比如说,压力。也就是说,此时我们可以任意变化系统的压力。而密度则是随着压力的变化而变化的。
既然我们已经知道在过渡区存在两个不同的相态,那么情况就不同了。我们多了一个约束,也就是说两相中的化学势相等。或者说,系统的路径总是沿着自由能最低的路径。
那么,根据这个约束条件,温度和压力两者就不再是独立的了,它只有一个是自由的。也就是说,系统的自由度少了一个,现在就只有一个自由度了。
- 当我们把温度确定下来时,压力也就随之确定了,这个压力就是蒸汽压。
- 当我们把压力确定下来时,温度也就随之确定了,这个温度就是沸点。
所以说,在两相并存的情况下,在一定的温度下,系统只可能有一个固定的压力。这就是蒸汽压。
5、麦克斯韦构建
我们已经解答了,在气液平衡下,一定的温度下只有一个固定的蒸汽压。那么这个蒸汽压是多少呢?这个问题的回答过程就叫做“麦克斯韦构建(Maxwell Construction)”。
也就是说,我们已经解释了,在实际的相变过程中,系统的路径是从 C 到 A 的水平直线,而不是范德华方程计算出来的 S 形曲线。那么这个水平直线的位置在何处?
伟大的麦克斯韦是第一个给出这个水平直线的构建方法的人。具体结果就是这样的:
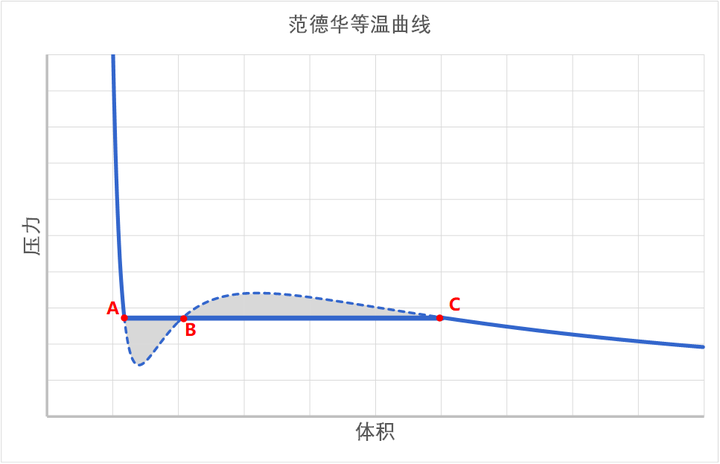
这条直线的位置,使得它与 S 形曲线围成的两块阴影面积相等。
为何是这样的呢?
因为在等温线上,从 A 到 C 所做的功就等于 AC 两点亥姆霍兹自由能之差。由于自由能是状态函数,所以它的差和路径应该是无关的。所以,从 A 到 C 之间所做的功——也就是 PV 图围成的面积,必须相等。
所以我们就找到了水平线 AC 的位置,它就是饱和蒸汽压。
6、最低自由能
我们可以用最小自由能的方法来分析一下这个相变的过程。理论上,系统可以沿着 1-2-3-4 这条曲线被连续压缩而不必有任何相变过程。但是,下面的分析讲告诉我们,这个过程的确不是一条自由能最低的过程。
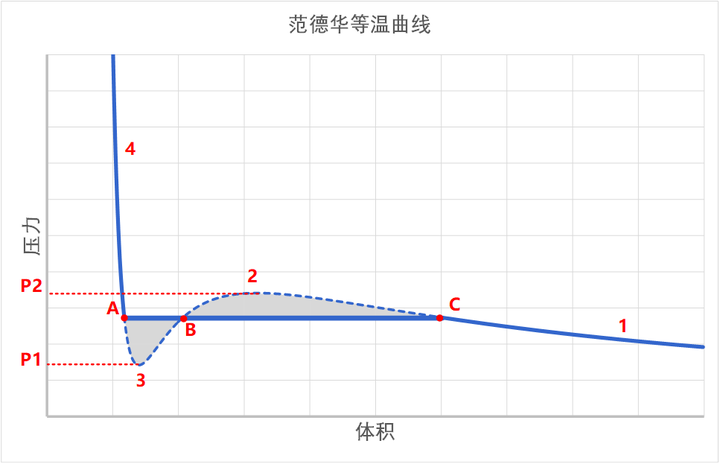
而在一个固定的温度下,自由能对压力的导数是:
首先,我们可以看 1-2 的压缩过程。在这个过程中,压力增加,而体积减小,因此我们可以知道,在 G-P 曲线中,这是一条上凸曲线。同理,3-4 的过程,也是一条上凸曲线,由于其体积要小得多,所以这条曲线的斜率要小得多。
而 2-3 过程,是一个压力下降,体积减小的过程。所以它是一条下凸曲线。
那么,整个过程中的自由能轨迹就很清楚了:
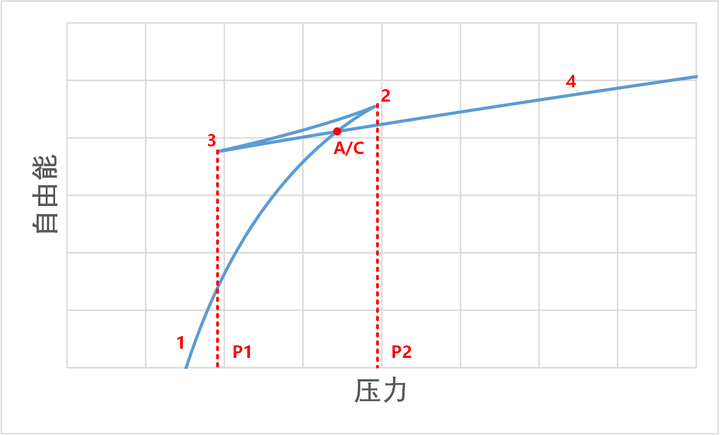
也就是说,如果是按照 S 形曲线压缩,整个过程中,自由能并不总是最小的。如果走最小路径,那么就要经过一个气 / 液自由能相等的点(也就是麦克斯韦构建的那条水平曲线)。
总而言之……
如果掰碎了讲,饱和蒸汽压的存在,并不是能一两句话讲明白的事情。实践中,我们其实只要知道,纯组分系统,在特定的温度下,两相平衡的时候,其压力是一个定值。这其实是等效于在一定压力下,其沸点是一个定值。因为系统都只有一个自由度。
至于多组分系统,就复杂得多了。其实日常烧水就是多组分系统(水、氮气、氧气系统)。所以在未达沸点的时候仍然可以蒸发,并且露点也可以很低。但是这些篇幅太长这里写不下……

 微信扫一扫
微信扫一扫 



