首先考虑对一个给定的图 G,对他的点进行染色,使得任意一条边的两个顶点不同色。我们把满足条件的最小的所需颜色数目叫做 chromatic number,记为
。
同时我们把图 G 中包含的最大完全图子图的点的数目叫做 clique number,记为
。很容易发现,一个 n 个点的完全图由于点两两相邻,至少需要 n 种不同的颜色。于是我们有如下结论:
Simple Observation:
由于我们更关心染色数的上界,到这里我们就会问,有没有
?很遗憾。。
Naive Conjecture:
Answer: False !
我认为百分之 80 的民科的证明就错在这里了:如果一个图不包含
即五个点的完全图为子图,不能得出这个图可以用四种颜色染色。
这里给一个例子:如下图考虑
,该图不包含
,因此
,但是
。
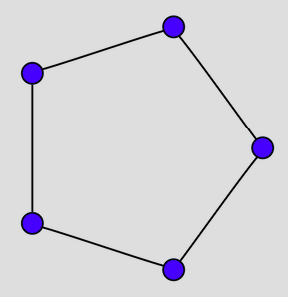
那么 chromatic number 能不能被 clique number 控制住呢?
Advanced Conjecture:
Answer (by Erdos, 1959): False !
实际上 Erdos 构造了 clique number 固定,但 chromatic number 任意大的图(Erdos-Renyi Graph)。也就是说在四色定理的证明中,试图从图中包含的完全子图的大小来讨论,是行不通的。更一般的,我们把满足
的图(并且所有 induced 子图也满足)叫做 perfect graph。对于这种图我们有更精细的结构:定义如果一个图 G 不包含长度大于 5 的 odd cycle 和它的 complement,我们称这个图 Berge。
Strong Perfect Graph Theorem (Chudnovsky, Robertson, Seymour, Thomas):
现在我们从 structure graph theory 的角度去看四色定理。delete an edge 指对 G 删去给定的边,contract an edge 指的是“商”去给定的边:将这条边的两个点粘合成一个并且保持所有和其他点的相邻关系(如下图)
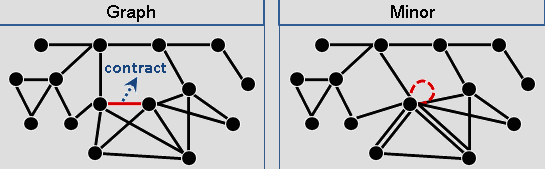
如果图 H 可以通过对 G deleting 和 contracting 一些边得到,我们就说 H 是 G 的 minor。可以发现 minor 关系是包含子图这个关系的推广:H 是 G 的子图,那么 H 也是 G 的 minor。
Graph Minor Theorem(Robertson, Seymour):
上面深刻的定理同时告诉我们,当图 G 对于给定的图 H minor-free 时,具有清晰的结构。具体定理的叙述太长这里就不说了,目前这个图结构引理的最新证明由 Kawarabayashi, Thomas, Wollen 在 2016 年简化到了 100 页以内。图的结构问题是图论中最困难的问题之一,有了图的结构,我们就可以考虑图上的染色问题了。比如对于一个没有
minor 的图,我们有 Wagner's Theorem,即 G 是由 planar graphs 和
经过 clique sum of order at most 3 得到的(如图),其中
指的是 8 个点的 cycle 再连上对径点。
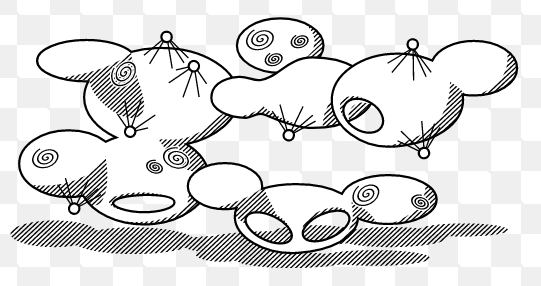
严格的说上图是 H minor-free 的图,里面的漩涡是 vortices。不过如果忽略漩涡,把洞当作
,还是可以看作是
minor-free 的图示的。
上面讲的 structure 内容看似和四色定理没什么关系。再让我们回到最开始举的
反例上:我们给它的 5 个点编号 1 到 5,如果我们 contract 边 12 和边 34,我们得到了
,也就是说
是
的 minor。这看起来也解释了
不能被
控制这个看似矛盾的现象:对于一个图 G,如果
是它的 minor,说明图 G 中有 t 个不相交的子集,分别 contract 掉它们我们可以得到
。那么对于那些子集,如果对所有子集我们首尾的点染色相同,那我们相当于在对
染色;否则我们就要求子集的首尾染色不同,相当于多了限制条件。换句话说,就算图 G 连
都不包含,但是如果它有
minor,那么有可能这个图需要至少 t 种不同的颜色。
很自然的,我们可以提出下面图论中最深刻的猜想:
Hadwiger's Conjecture:
配合 planar graph 的经典定理:
Kuratowski's Theorem:
我们可以发现,四色定理实际上是 Hadwiger's Conjecture 的 t=4 时的特殊情况。目前对这个猜想的进展如下:
Trivial
Hadwiger, 1943
By computer, 1976 (即 四色定理)
Robertson, Seymour, Thomas, 1993
Open
注意到 Robertson, Seymour and Thomas 对 t=5 情形的证明没有用电脑,但是用到了四色定理的结论。如果有一天有人可以证明 Hadwiger's Conjecture,绝对是组合数学里面最大的新闻了。目前这个猜想大家都认为是对的,但是我们目前的工具不够深刻。
做为结束,还是回到四色定理。四色定理有没有不依赖计算机的证明?答案是没有,不过目前已经可以通过计算机在 10 秒内证完了。如果得到了四色定理不依赖计算机的证明,对 Hadwiger's Conjecture 绝对是巨大的推进,发个四大不是问题。

 微信扫一扫
微信扫一扫 



