如果没有发明弧度制，sin 的导数还是 cos 吗?_网络百科

高赞的回答都是什么情况，回答题主的问题了吗……介绍了一遍角度制和弧度制的来历，又复制了一遍三角函数的定义，然后突然说 sin 的导数当然还是 cos，我寻思这也没回答问题啊，别人问什么你给他推一遍不就好了。

在高中我第一次学到弧度制时，我也在想为什么要这么定义。我们先来看现在的弧度制定义：指用弧长与半径之比度量对应圆心角角度的方式。用符号 rad 表示，读作弧度。等于半径长的圆弧所对的圆心角叫做 1 弧度的角。

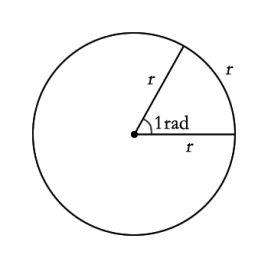
如果说是因为角度制含有单位不便于进行数学计算倒还能理解，但估计很多人思考过：为什么要这么定义？这样定义导致我们学习三角函数时铺天盖地的

$\pi$

出现，本来也就小学学圆的周长和面积接触过

$\pi$

，初中都没怎么碰到过，结果一上高中学了弧度后

$\pi$

就从高中一直写到了大学，折磨了同学们好多年。

况且，如果角度制是因为含有度这个单位而在数学中被放弃，我们完全可以定义一种新的度制，比如说叫丁真度制，因为它的定义很纯真，令 1 丁真度=1 角度（也就是 1°），在这种新的制度定义下，这样有

$sin30=\frac{1}{2}，sin45=\frac{\sqrt{2}}{2}，sin60=\frac{\sqrt{3}}{2}$

，完全和生活中用的一致，只是去掉度的单位就行了，方便快捷。

那么为什么要发明弧度制这种古怪的定义方式呢？我们可以看到一般在介绍完弧度制的定义后，通常有这么一句话：

“弧度制的精髓就在于统一了度量弧与角的单位，从而大大简化了有关公式及运算，尤其在高等数学中，其优点就格外明显。”

所以一个事物出现存在并得到公认使用至今一定是有它的道理，弧度制这种定义方式最大的优点是简化运算，尤其是在高等数学中！我们接下来来研究下这个问题。

虽然函数的自变量和因变量可以不一定是数集，但是为了在数学中方便计算，对于三角函数这种重要函数，需要将其定义为一个数集的到另一个数集的映射。像我们之前说的，如果非要想使用角度制进行运算，那我们就令 1 丁真度=1 角度，这样自变量集合就是数集了。这时的问题就是为什么要采用弧度制而不是我刚刚提出的丁真度制？我们全面地看待这个问题。

定义：一个周角的大小的

$\frac{1}{a}$

为 1 坤度（a>0），这种方式叫坤度制。

我甚至都没限制 a 一定要大于 1，也就是说哪怕 1 坤度比周角大我们都甚至可以拿进来讨论。我们接下来就是来研究这个 1 坤度取多少是最合适的。易知：当

$a=2\pi$

时，坤度制就是弧度制，因为一个圆周的

$\frac{1}{2\pi}$

就是半径长的圆弧，此时对应的角度就是 1rad；当

$a=360$

时，坤度制就是我们前面定义的丁真度制，因为一个圆周的

$\frac{1}{360}$

就是 1°也就是 1 丁真度。

那其实我们就是在研究这个 a 为什么取 2π是最佳的，取其他数值都不合适。

以下均只涉及 sin 和 cos，因为 tan，csc，sec，cot 都能根据 sin 和 cos 推出来。

首先我们能得出一些显然的结果：

$\frac{a}{4}$

坤度就是我们常说的 90°，

$\frac{a}{2}$

坤度就是 180°，

$a$

坤度就是 360°

根据三角函数定义，我们有

$sin(2k\cdot\frac{a}{4})=0,sin[(4k+1)\cdot\frac{a}{4}]=1,sin[(4k-1)\cdot\frac{a}{4}]=-1,cos[(2k+1)\cdot\frac{a}{4})]=0,cos[4k\cdot\frac{a}{4}]=1,cos[(4k+2)\cdot\frac{a}{4}]=-1,k\in Z$

根据三角函数的定义，依旧有

$sin^2\alpha+cos^2\alpha=1$

等等那一系列恒等式，依旧有

$sin(-\alpha)=-sin\alpha,cos(-\alpha)=cos\alpha$

根据三角函数定义，有诱导公式：

$sin(\alpha+\frac{a}{4})=cos\alpha$

$cos(\alpha+\frac{a}{4})=-sin\alpha$

……其他的一大堆就不列出来了，反正也是奇变偶不变，符号看象限

根据单位圆的向量证明方法依旧能证明

$cos(\alpha-\beta)=cos\alpha cos\beta+sin\alpha sin\beta$

，进而由诱导公式依旧能推出

$cos(\alpha+\beta)=cos\alpha cos\beta-sin\alpha sin\beta$

$sin(\alpha+\beta)=sin\alpha cos\beta+cos\alpha sin\beta$

$sin(\alpha-\beta)=sin\alpha cos\beta-cos\alpha sin\beta$

进而也有二倍角公式

$sin2\alpha=2sin\alpha cos\alpha，cos2\alpha=cos^2\alpha-sin^2\alpha=2cos^2\alpha-1=1-2sin^2\alpha$

由此半角公式、多倍角公式成立；和差化积公式、积化和差公式成立；正弦定理依旧成立；由向量的点积和诱导公式，余弦定理依旧成立；反三角函数依旧成立，就是改变下值域而已；以此可推辅助角公式依旧成立。

圆的面积依然是

$\pi r^2$

，圆的周长依旧是

$2\pi r$

，这个显然不会变。对于一个圆心角是

$\theta$

坤度的扇形，它的面积公式

$S=\frac{\theta}{a}\cdot\pi r^2$

，弧长公式

$l=\frac{\theta}{a}\cdot2\pi r$

。

细心的小朋友可能发现了：当是弧度制时，也就是

$a=2\pi$

，

$S=\frac{\theta r^2}{2}\$

，

$l=\theta r$

，当然也可以写成

$S=\frac{lr}{2}$

；当是丁真度制时，也就是

$a=360$

，

$S=\frac{\theta\pi r^2}{360}$

，

$l=\frac{\theta\pi r}{180}$

，当然也可以写成

$S=\frac{lr}{2}$

。这不恰好就是我们高中背过的弧度制和角度制下的扇形面积公式和弧长公式吗？！所以其实他们都可以说来源于一个式子。

由此可以发现，其实在高中阶段，如果改变弧度制的定义，依旧不影响大部分公式的计算，也就影响扇形的面积和弧长公式。这也是为什么许多人没有理解到弧度制发明的意义。但其实学到高等数学时，就能发现问题了。

对于一个单位圆上，圆心角为 x 的扇形：

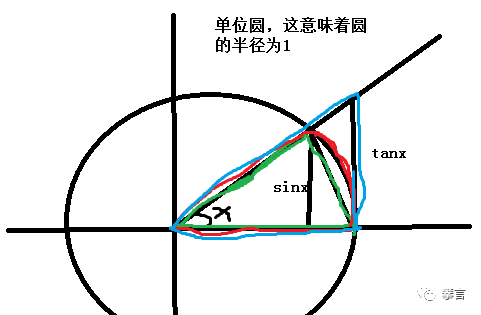
由我们前面的扇形面积公式可知该圆心角对应的红色扇形面积为

$\frac{\pi x}{a}$

绿色三角形的面积显然为

$\frac{sinx}{2}$

蓝色三角形的面积显然为

$\frac{tanx}{2}$

当 x 从正方向趋于 0 时，显然一定有

$0<\frac{sinx}{2}<\frac{\pi x}{a}<\frac{tanx}{2}$

，将该不等式全部乘以

$\frac{2}{sinx}$

即有

$cosx<\frac{asinx}{2\pi x}<1$

因为

$\lim\limits_{x\to0^+}cosx=1$

，所以

$\lim\limits_{x\to0^+}\frac{asinx}{2\pi x}=1$

，即

$\lim\limits_{x\to0^+}\frac{sinx}{x}=\frac{2\pi}{a}$

因为

$\frac{sinx}{x}$

是偶函数，所以

$\lim\limits_{x\to0}\frac{sinx}{x}=\frac{2\pi}{a}$

神奇吧，原来我们高数学的第一个基本极限就开始出现问题了！由此我们还能继续推：

$\lim\limits_{x\to0}\frac{1-cosx}{\frac{1}{2}x^2}=\lim\limits_{x\to0}\frac{2sin^2\frac{x}{2}}{\frac{1}{2}x^2}=\lim\limits_{x\to0}\frac{2\cdot(\frac{2\pi}{a}\cdot\frac{x}{2})^2}{\frac{1}{2}x^2}=\frac{4\pi^2}{a^2}$

仅仅是这个极限，就已经计算量开始变大了，最关键的是它和

$\lim\limits_{x\to0}\frac{sinx}{x}$

居然还不一样！

$\lim\limits_{x\to0}\frac{tanx}{x}=\lim\limits_{x\to0}\frac{tanx}{sinx}\cdot\frac{2π}{a}=\lim\limits_{x\to0}\frac{1}{cosx}\cdot\frac{2π}{a}=\frac{2π}{a}$

对于

$\lim\limits_{x\to0}\frac{arcsinx}{x}$

，令

$x=sint$

，则变为

$\lim\limits_{t\to0}\frac{t}{sint}=\frac{a}{2\pi}$

对于

$\lim\limits_{x\to0}\frac{arctanx}{x}$

，令

$x=tant$

，则变为

$\lim\limits_{t\to0}\frac{t}{tant}=\frac{a}{2\pi}$

而对于

$\lim\limits_{x\to0}\frac{ln(1+x)}{x}$

、

$\lim\limits_{x\to0}\frac{e^x-1}{x}$

倒确实是严格等于 1。至于其他的什么

$\lim\limits_{x\to0}\frac{x-sinx}{x^3}$

、

$\lim\limits_{x\to0}\frac{tanx-x}{x^3}$

这种结果算出来更是缤纷多彩，大家可以自行计算，答主算不动了。

为什么算上面的极限我们暂时不能用洛必达法则呢，因为我们还没算导数呢。接下来就是最激动人心的算导数环节。

$\frac{dsinx}{dx}=\lim\limits_{\Delta x\to0}\frac{sin(x+\Delta x)-sinx}{\Delta x}=\lim\limits_{\Delta x\to0}\frac{sinx cos\Delta x+cosxsin\Delta x-sinx}{\Delta x}=\lim\limits_{\Delta x\to0}\frac{sinx (cos\Delta x-1)+cosxsin\Delta x}{\Delta x}=\frac{2\pi}{a}cosx$

至此，我们可以说回答了题主的问题，sinx 的导数是 cosx 的形式，但是前面的系数取决于你规定的弧度制！同理我们有：

$\frac{dcosx}{dx}=\lim\limits_{\Delta x\to0}\frac{cos(x+\Delta x)-cosx}{\Delta x}=\lim\limits_{\Delta x\to0}\frac{cosx cos\Delta x-sinxsin\Delta x-cosx}{\Delta x}=\lim\limits_{\Delta x\to0}\frac{cosx (cos\Delta x-1)-sinxsin\Delta x}{\Delta x}=-\frac{2\pi}{a}sinx$

cosx 的导数也是 -sinx 的形式，但是前面还有个系数。tanx、cscx、secx、cotx 还有反三角的导数我就不算了，反正都能自己推出来。

接下来更令人迷惑的还有幂级数展开，由以上我们推出来的，能得到：

$sinx=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}(\frac{2\pi}{a})^{2n+1}x^{2n+1}$

$cosx=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n)!}(\frac{2\pi}{a})^{2n}x^{2n}$

众所周知：

$e^x=\Sigma_{n=0}^\infty\frac{1}{n!}x^n$

，所以

$e^\frac{2\pi ix}{a}=\Sigma_{n=0}^\infty\frac{1}{n!}(\frac{2\pi ix}{a})^n=\sum_{n=0}^{\infty}\frac{1}{(2n+1)!}(\frac{2\pi}{a})^{2n+1}(ix)^{2n+1}+\sum_{n=0}^{\infty}\frac{1}{(2n)!}(\frac{2\pi}{a})^{2n}(ix)^{2n}=i\cdot\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}(\frac{2\pi}{a})^{2n+1}x^{2n+1}+\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n)!}(\frac{2\pi}{a})^{2n}x^{2n}=isinx+cosx$

也就有了欧拉公式：

$e^\frac{2\pi ix}{a}=isinx+cosx$

，平常大家还说欧拉公式完美呢，这下多了这么大一坨，可想而知如果这个 a 是 360 或者别的什么数，那算着得多恶心。不过令

$x=\frac{a}{2}$

, 依旧有恒等式

$e^{\pi i}+1=0$

这个神奇的结论。

因此我们有

$e^{-\frac{2\pi ix}{a}}=cosx-isinx$

，进而得到两个基本的方程

$cosx=\frac{e^\frac{2\pi ix}{a}+e^{-\frac{2\pi ix}{a}}}{2}$

，

$sinx=\frac{e^\frac{2\pi ix}{a}-e^{-\frac{2\pi ix}{a}}}{2i}$

，如果 a 没有一个良好的数值，这个欧拉公式会很复杂。由此推理下去，完全可以预料，如果没有弧度制令 a 取 2π，那么将会对高等数学、微积分、复变函数与积分变换、微分方程、概率论与数理统计、随机过程等数学学科产生深远的影响，对于后人接触初等以上的数学不利。

首先 sinx 和 x、tanx 和 x 等极限就不是等价无穷小，必须要带一个系数才是，显然对于刚接触极限的人来说比较烦恼，不够方便，其次 sinx 的导数不再是 cosx，前面必须要带一个系数，对于学习微积分的人来说，十分痛苦，本来当年背导数表和积分技巧就挺痛苦的了，这下不用弧度制了，还得记住那个不好记的系数，然后在学习泰勒展开时，发现 sinx 和 cosx 的幂级数还有一个系数的高次求和，关键他还在求和符号里面，随着项数增多它的次方还越大。如果以上都还能接受就算了，关键它直接影响到了欧拉公式，这让学复变的同学更加头痛了。

因此，人们最终选择了弧度制，也就是令

$a=2\pi$

，也就是规定周角的

$\frac{1}{2\pi}$

为 1rad。因为只有弧度制时，以上所有公式都将变得简洁，方便人们运算，方便后来者学习。

如果没有发明弧度制，sin 的导数还是 cos 吗?

相关推荐